География и геология/ 7.Техника и технология
геологоразведочных работ
Д. г.-м. н.
Исаев В.И.
Томский
политехнический университет, Россия
Определение первоочередных скважин на нефтегазоперспективной структуре
по данным гравиразведки
Латеральная зональность плотности
(пористости) пород и трехмерность объектов. Главной закономерностью изменения плотности s отложений отдельных свит и толщ является
экспоненциальное увеличение с глубиной залегания Z [1]. Вместе с тем, свиты и толщи обладают и
латеральной литофизической неоднородностью, причем скопления, залежи углеводородов
(УВ), как правило, приурочены к высокопористым литофизическим неоднородностям
(1–3 км и более). Такие неоднородности имеют дефицит плотности до 0,08 г/см3
и более.
Сейсморазведка, как базовое средство
структурного обоснования ловушки УВ, из-за сложных сейсмогеологических условий,
имеет ограниченные возможности по прогнозированию геологического разреза. В
связи с этим рациональным представляется моделирование распределения плотности
(пористости) объектов, опоискованных сейсморазведкой, в гравитационном поле.
При этом, необходимо учитывать универсальные свойства этих объектов:
вертикальный градиент плотности и трехмерность.
Предлагается на локальных структурных
формах, выявленных сейсморазведкой, проводить объемное (трехмерное) плотностное
моделирование на основе решения обратной линейной задачи гравиметрии. Это
позволит выявлять аномалии плотности в пределах сейсмического тела – области
разуплотнения, отождествляемые с высокопористыми литофациальными разностями.
Алгоритмы трехмерного моделирования. Математическая
модель интерпретации при трехмерном моделировании может быть представлена в
виде системы линейных уравнений:
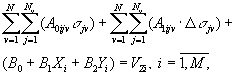 (1)
(1)
а
также системы линейных двусторонних неравенств
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
где N – число (сейсмических) слоев моделируемой среды; Nv – количество аппроксимирующих блоков в v-м слое; sjv, Dsjv – постоянные составляющие плотности и вертикальные
градиенты плотности аппроксимирующих блоков, подлежащие определению; A0ijv, A1ijv –
гравитационное влияние на i-ю расчетную точку j-го аппроксимирующего блока из v-го слоя
при плотности и градиенте плотности, равных единице; B0, B1, B2 –
коэффициенты линейной функции, аппроксимирующие региональный фон, подлежащие
определению; Xi, Yi – координаты расчетных точек сети наблюдений ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() – нижние и верхние предельные значения постоянных
составляющих плотностей, вертикальных градиентов плотностей и коэффициентов
линейной функции – количественная мера априорной геолого-геофизической
информации о моделируемых параметрах.
– нижние и верхние предельные значения постоянных
составляющих плотностей, вертикальных градиентов плотностей и коэффициентов
линейной функции – количественная мера априорной геолого-геофизической
информации о моделируемых параметрах.
Для решения системы (1)–(4) применен метод
сопряженных градиентов, выполненный в виде итерационного процесса [2].
В
качестве аппроксимирующего блока принимается
вертикальная четырехугольная призма с произвольной ориентировкой оснований и
плотностью, линейно меняющейся с глубиной (рис. 1). При такой аппроксимации
латеральные изменения плотности слоев и тектонические нарушения учитываются
представлением слоя латеральным рядом геоблоков разной плотности (рис. 1, б). Плотность задается на верхнем и
нижнем основаниях блоков значениями s1 и s2 – на
серединах отрезков, образующих верхнее и нижнее основания вертикальной трапеции
(например, трапеции DCCIDI, рис. 1, а),
что удобно для последующих вычислений.
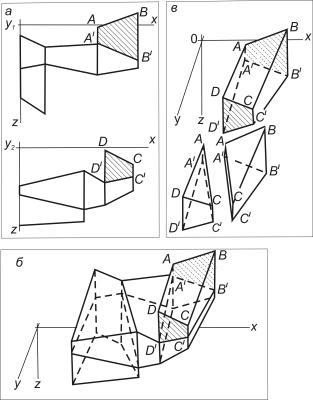
Рис.
1. Плотностная параметризация при объемном (трехмерном) моделировании
блоково-градиентно-слоистых сред: а) исходное описание вертикальными сечениями;
б) описание аппроксимирующими блоками; в) аппроксимирующий блок и
технологические элементы
Поверхность ABCD (рис. 8, в)
в общем случае не плоская. Аналитическое решение прямой задачи гравиметрии для
выделенного технологического элемента (треугольной призмы) получено и
алгоритмизировано в работе [3].
Интерпретация данных высокоточной
гравиразведки на Верхненышском газоконденсатном месторождении Сахалина. Основой для геометрической параметризации изучаемой
среды послужили структурные схемы сейсмогоризонтов по кровле окобыкайских отложений
(ok) – УОСГ-I и кровле дагинских отложений (dg) – УОСГ-II [4]. На основе структурных схем отстроены 12
глубинных сечений. Затем, пространство между вертикальными срезами структур
было заполнено 492 аппроксимирующими блоками. Априорным плотностям
аппроксимирующих блоков приписывались нормальные значения s(Z). В качестве наблюденного поля послужили результаты
высокоточной гравиметрической съемки – ±0,10 мГл.
Результаты
решения задачи приведены на рисунках 2–3. Точность подбора поля – ±0,10 мГл. Рассчитанное
распределение плотности находится в пределах заданных ограничений. Результаты
моделирования хорошо согласуются с результатами геофизических исследований и испытаний
глубокой скважины Верхне-Нышская 1.
Очевидны
рекомендации по положению последующих скважин – на участках максимальных разуплотнений, с
учетом структурного и гипсометрического факторов. Первоочередная последующая
скважина рекомендуется на вскрытие верхних
горизонтов нефтегазоносных окобыкайских
отложений на северо-восточном крыле структуры.

Рис.
2. Горизонтальный срез Верхне-Нышской структуры по верхней части
окобыкайских отложений (приведены изогипсы по кровле окобыкайских отложений):
1) изогипсы УОСГ, км; 2) разрывные нарушения; 3) скважина Верхне-Нышская 1; 4)
горизонтальные сечения аппроксимирующих блоков при объемном моделировании;
выявленные разуплотнения (5, 6) более чем на 0,03 и 0,05 г/см3,
соответственно
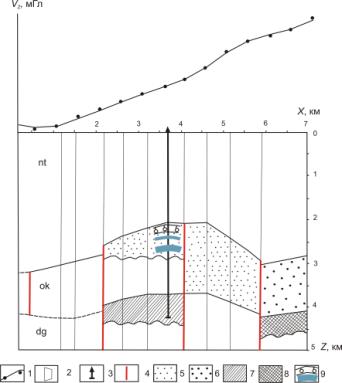
Рис.
3. Вертикальный
срез Верхне-Нышской структуры вдоль профиля 7: 1) наблюденное и расчетное поля;
2) вертикальные сечения аппроксимирующих блоков при объемном моделировании; 3)
скважина Верхне-Нышская 1; 4) разрывные нарушения; выявленные разуплотнения (5,
6) и уплотнения (7, 8) более чем на 0,03 и 0,05 г/см3,
соответственно; 9) залежи газа и конденсата, водонасыщенные интервал
ЛИТЕРАТУРА
1.
Исаев
В.И. Интерпретация данных гравиметрии и
геотермии при прогнозировании и поисках нефти и газа – Томск: Изд-во ТПУ, 2010.
– 172 c.
2.
Старостенко В.И.
Устойчивые численные методы в задачах гравиметрии – Киев: Наук. думка, 1978. –
228 с.
3.
Исаев В.И., Пятаков Ю.В.
Решение прямой задачи гравиметрии для трехмерных блоково-градиентно-слоистых
сред // Геофизический журнал. – 1990. – Т. 12. – № 3. – С. 72–79.
4.
Исаев В.И., Шпакова
Н.В., Исаева О.С. Распределенный банк геолого-геофизических данных по нефти и
газу Сахалинской области // Тихоокеанская геология. – 2003. – Т. 22. – № 2. –
С. 81–91.