Строительство и архитектура /3. Современные технологии строительства, реконструкции и  реставрации.

к.т.н. Шишов И.И., к.т.н. Репин В.А, Грешкина Е.В.

Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, Россия

Расчет стержневых систем с учетом продольных сил в стержнях

Рассматриваются плоские системы, состоящие из вертикальных и горизонтальных элементов, жестко или шарнирно соединенные между собой в узлах. Это могут быть, например, каркасы зданий. Вертикальные элементы (колонны) обычно испытывают продольно-поперечный изгиб и деформируются геометрически нелинейно. Несущая способность каркаса может быть ограничена не только прочностью, но и предельно допустимыми перемещениями или возможной потерей устойчивости. Расчет такой системы может быть выполнен в конечно-разностной форме. Стержни разбиваются на малые участки, для которых записываются условия равновесия и уравнения совместности деформаций в виде основного дифференциального уравнения упругой линии [1].

Где М- изгибающий момент в поперечном сечении,

EJ-изгибная жесткость стержня.

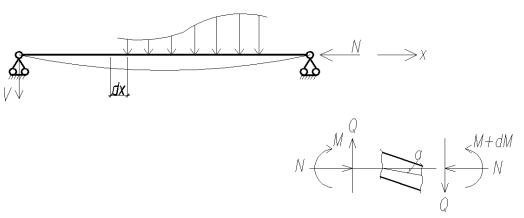
Рис. 1. Продольно-поперечный изгиб стержня

Вторая производная функция перемещений (рис.1) записывается в разностной форме. Связь между внутренними усилиями в поперечном сечении М, Q, N устанавливается с учетом возникающих деформаций и перемещений [2]

Этим и учитывается геометрическая нелинейность деформирования.

Такое решение для стержня прошло достаточную проверку [3]. Определялись усилия, возникающие в опорных связях от единичных угловых и линейных перемещений концов, сравнивались со значениями, взятыми из таблиц для расчета рам на устойчивость; прогибы стержней при одновременном действии продольной силы и поперечной нагрузке сравнивались с решениями И.А. Биргера [2]; определялись критические силы для центрально сжатого упругого стержня. Во всех случаях получалось хорошее совпадение результатов. Для системы в целом принимаются известные предпосылки метода перемещений:

продольной деформацией стержня, а также сближением его концов при изгибе можно пренебречь;

концы стержней, соединенные одним жестким узлом, при деформировании системы поворачиваются на один и тот же угол.

формируется основная система метода перемещений. Для каждой из введенных линейных и защемляющих связей определяется усилие, дающее единичное перемещение в направлении этой связи. Далее последовательно многократно определяются усилия, возникающие во введенных связях от внешней нагрузки, и перемещения в направлении каждой из них корректируются так, чтобы усилие было равно нулю. Решение заканчивается, когда необходимость в коррекции отпадает.

Для проверки алгоритма и программы были определены критические нагрузки для П-образной рамы при жестком и шарнирном соединении ригеля с колоннами. Значения отличались от полученных по формулам Эйлера менее, чем на 1%.

Исследовательские расчеты выполнялись для трехэтажной рамы из железобетона (рис.2).

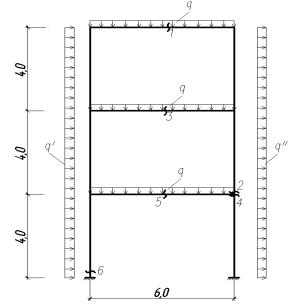
Рис.2 Нагружение и опасные сечения рамы

Колонны имеют сечение 300х300 мм, симметричное армирование, µ=µ^/=0,0131, предельный момент М_п=0,1068 МН×м, жесткость на изгиб 20,25 МН×м². Сечение ригелей 300х600 мм, симметричное армирование, µ=µ^/=0,0155, предельный момент М_п=0,4928 МН×м, жесткость на изгиб 162 МН×м². Нормативная ветровая нагрузка принята равномерно распределенной по высоте каркаса: с наветренной стороны q^/=0,0018 МН/м, с подветренной q^//=0,0014 МН/м; коэффициент надежности γ_f=1,4. Интенсивность вертикальной нагрузки q на всех этажах одинакова; коэффициент надежности γ_f=1,2. Рассматривались четыре конструктивные схемы:

схема 1 -- все узлы каркаса жесткие;

схемы 2,3,4 -- один из ригелей: верхний, средний или нижний соответственно присоединяется к колоннам шарнирно.

Из расчетов на прочность определялись предельно допустимые расчетные вертикальные нагрузки q_u при одинаковых горизонтальных расчетных нагрузках q^/=0,0025 МН/м, q^//=0,002 МН/м. Из расчетов по деформациям определялись предельно допустимые нормативные вертикальные нагрузки q при нормативных ветровых нагрузках q^/=0,0018 МН/м, q^//=0,0014 МН/м. Предельно допустимое горизонтальное перемещение верха колонны Δ_u=24мм. Определялись критические значения вертикальной нагрузки q при нормативной нагрузке от ветра ( в качестве критической фиксировалась интенсивность нагрузки при которой горизонтальные перемещения верха каркаса, постепенно и все более стремительно увеличиваясь при увеличении нагрузок, достигают больших значений (до 4 м) или становятся отрицательными). Результаты расчетов приводятся в таблице 1.

Таблица 1

	Расчеты на прочность			Расчеты по деформациям		Критическая нагрузка
Конструктивная схема №	u,МН/м	Max М/Мu:для ригеля, для стойки	Сечение № (рис.2)	qu, МН/м	maxΔ/Δu	qкр,МН/м
1	0,1	0,715 1,016	1 2	0,9	1,005	1,37
2	0,09	0,822 0,964	1 2	0,9	1,00	1,37
3	0,1	0,913 0,965	3 4	0,2	1,021	0,98
4	0,11	1,004 0,942	5 6	0,0	1,065	0,9

Алгоритм и составленная по нему программа дают возможность получать решения для плоской стержневой системы с жесткими или шарнирными узлами с заданным запасом прочности, жесткости и устойчивости.

Литература:

1. Малышев М.В., Шишов И.И. Исследование сжатия с изгибом на основе дифференциальных связей между внутренними усилиями// Материалы III всероссийской конференции.-Чебоксары, 2001.-с.81-86.

2. Биргер И.А. Продольно-поперечный изгиб стержней. Прочность, устойчивость, колебания.-Т.1.-М.: Машиностроение, 1968.-с.229-236.

3. Шишов И.И. Определение несущей способности сжато-изогнутой сваи в вечномерзлом грунте .// Основания, фундаменты и механика грунтов.-- 2 010. -- №4.-- с.15-18.