Строительство и
архитектура. Современные технологии
строительства, реконструкции и
реставрации.
Ст-т
Курбатов Ю.Е., к.т.н. Кузнецова С.Г.
Пермский
национальный исследовательский
политехнический университет, Россия
Выравнивание моментов
в неразрезной балке
с упругой опорой.
Для балки (см. рис. 1) требуется определить
упругую характеристику опоры 1, т. е. коэффициент податливости (
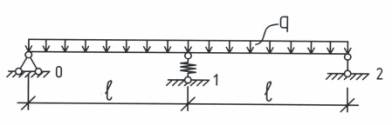
Рис. 1. Заданная система
Для решения поставленной задачи используем метод
сил. Заданная система один раз статически неопределима (см. рис. 2).
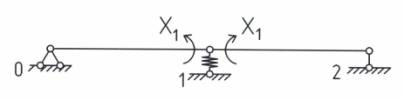
Рис. 2. Основная система
Из канонического уравнения метода сил 
.
При определении коэффициента 
необходимо учесть
величину упругого прогиба 
и угол поворота 
(см. рис. 3).
Рис. 3. Величина
упругого прогиба и угол поворота балки при действии 
=1.
Коэффициент 
находим при помощи
эпюры 
(см. рис. 4).
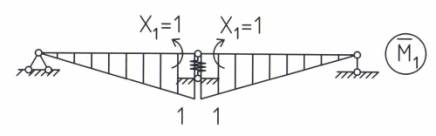
Рис. 4. Эпюра моментов от действия единичного
момента 
.
По аналогии находим коэффициент 
, учитывая величину упругого
прогиба 
, угол поворота 
(см. рис. 5) и используя эпюру 
(см. рис. 6):
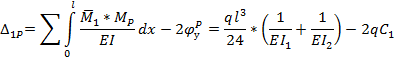
Рис. 5. Величина упругого прогиба и угол
поворота балки при действии внешней нагрузки.
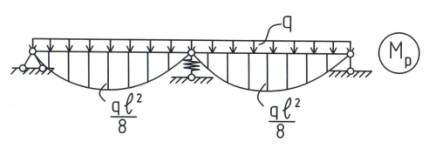
Рис.
6. Эпюра моментов от действия внешней нагрузки.
Пусть К =
. Тогда 
Окончательная эпюра
моментов примет следующий вид:
Рис. 7. Окончательная эпюра моментов.
Найдем значение
опорного момента:
Пусть z =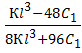
. Тогда 
(1)
Найдем значение
максимального момента:
, т. е. 
.
(2)
Из условия задачи 
. С учетом выражений (1) и (2), получим:
(при этом 
) (3)
Из выражения (3) найдем 
.
С учетом ранее сделанной замены, получим: z
=
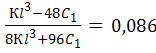. Коэффициент податливости будет равен: 
(4)
Сравним значения 
для двух
железобетонных балок разного сечения
(см. рис.8) при условии, что для обеих балок:
; 
; 
Рис. 8. Сравниваемые сечения.
С учетом моментов инерции прямоугольного и
круглого сечений и формулы (4) получим:
; 
.
Следовательно, балка круглого сечения при прочих
равных условиях ведет себя менее упруго, т.к. коэффициент податливости при ее
использовании имеет меньшее значение.
Литература:
Строительная
механика. Общий курс : учебник для вузов / В. А. Киселев .— 4-е изд., перераб.
и доп .— Москва : Стройиздат, 1986 .— 520 с.