Технические науки/10. Горное дело

К.г.-м.н. Песков А.В., к.т.н. Ольховская В.А., Зенин В.И.

Самарский государственный технический университет, Россия

ИССЛЕДОВАНИЕ ПРОНИЦАЕМОСТИ ГОРНЫХ ПОРОД ПО ГАЗУ И УЧЁТ ЭФФЕКТА КЛИНКЕНБЕРГА В ТЕОРИИ СТАЦИОНАРНОЙ ФИЛЬТРАЦИИ

Измерение газопроницаемости горных пород на образцах керна, полученного при разведочном бурении, играет важную роль в оценке фильтрационно-емкостной характеристики пластов-коллекторов, покрышек и локальных флюидоупоров. Вместе с данными геофизических исследований скважин такая информация используется для подсчёта запасов в природных резервуарах углеводородов и объектного мониторинга недр при эксплуатации подземных хранилищ газа. От проницаемости пород, играющих роль покрышек, зависят их герметичность и миграция углеводородов. В свою очередь, экранирующая способность флюидоупоров позволяет соотнести литолого-стратиграфические комплексы в разрезе скважины с гидродинамическими и рассматривать некоторые залежи как «капиллярно-экранированные».

Течение вязких однородных жидкостей через изотропные пористые среды, проницаемость которых может считаться скалярной величиной, в стандартных фильтрационных экспериментах обычно подчиняется классическому закону Дарси

, (1)

где q – объёмный расход жидкости; k – проницаемость пористой среды вдоль оси образца; F - площадь поперечного сечения образца; - длина образца; μ – динамическая вязкость жидкости; Р_А-Р_В - разность давлений на концах образца.

Если исследуется фильтрация газообразного флюида, то при больших расходах закон Дарси нарушается. Это обусловлено возникновением в порах локальных явлений турбулентности и дополнительными потерями давления, пропорциональными квадрату скорости фильтрации при движении флюида по извилистым каналам. Устанавливая режимы, исключающие подобный эффект и обеспечивающие линейность связи «расход – градиент давления», можно ожидать, что закон Дарси будет справедлив и для газа. Если под q подразумевать объёмный расход, отнесённый к среднему давлению в образце , то

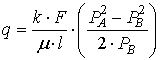. (2)

Закон Дарси в дифференциальной форме для линейного течения имеет вид

, (3)

где - объёмная скорость газа, отнесённая к среднему давлению в образце.

На основании уравнения (3) с учётом условия неразрывности и уравнения состояния идеального газа получают дифференциальное уравнение стационарной фильтрации

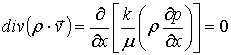, (4)

где ρ – плотность газа при давлении p.

Уравнения (2) и (4) предполагают, что инерционность потока незначительна по сравнению с вязкостью газа, а размер пор больше среднего свободного пробега молекул газа. Иными словами, движение газа через пористый материал при умеренных скоростях, подобно движению жидкости, включает лишь один механизм – вязкое течение. В таких случаях проницаемость, измеренная по газу, приближается к проницаемости, измеренной по жидкости [4].

Исследованиями Л.Клинкенберга [1] впервые было установлено, что проницаемость пород по газу k_г может быть выше проницаемости по жидкости k_ж. Это объясняется эффектом проскальзывания газа в условиях, когда длина среднего пробега молекул газа соизмерима с диаметром капилляра (если считать, что поры имеют трубчатую цилиндрическую форму).

Величина газопроницаемости связана с внутрипоровым давлением [2], формально эта связь выражается в виде:

k_г = k_ж · (1 + b/р_ср), (5)

где b - константа Клинкенберга (коэффициент скольжения); p_ср - среднее давление при определении газопроницаемости.

Для пор очень малого размера и для газов при пониженном давлении уравнения (2) и (4) неприменимы. При наличии скользящего течения закон Дарси записывается с учётом эффекта Клинкенберга:

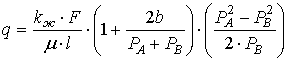, (6)

а дифференциальное уравнение стационарной фильтрации газа принимает вид

. (7)

Если, измеряя проницаемость, варьировать значения давления на концах образца породы и поддерживать скорость фильтрации газа в каждом опыте постоянной, то можно получить зависимость кажущейся проницаемости от величины 1/p_ср, обратной среднему давлению (график Клинкенберга). Значение проницаемости k_∞ при давлении р_ср→∞ отождествляется с истинным, при котором отсутствует скольжение газа. Это значение, согласно (5), совпадает с проницаемостью k_ж по жидкости, не реагирующей с веществом коллектора, и не зависит от природы газа.

Константа Клинкенберга и проницаемость по жидкости связаны соотношением

b = В · k_ж^-С, (8)

где В и С – постоянные числовые коэффициенты.

Приближённо константу Клинкенберга можно рассчитать [3] с помощью уравнения

b = 0,77 · k_ж^-0,39. (9)

Экспериментальные данные по определению газопроницаемости, которые были приведены в работе [5], подтвердили, что эффект проскальзывания газа (воздуха) тем больше, чем меньше коэффициент проницаемости горных пород и перепад давления.

Целью дополнительной серии экспериментов явилось изучение газопроницаемости пород при низких (менее 0,2 МПа) перепадах давления на установках «Дарсиметр» и «Экопласт», а также определение погрешности измерения проницаемости. На установке «Дарсиметр» газопроницаемость по воздуху определялась при поровом давлении до 0,2 МПа и давлении обжима керна 1 МПа, с низкой базовой погрешностью. На установке «Экопласт», позволяющей моделировать пластовые условия, газопроницаемость породы изучалась при поровом давлении до 0,3 МПа и давлении обжима до 31 МПа. Исследования проводились на эталонном корунде, карбонатных и терригенных образцах пород. Минимальный перепад давления составлял 0,02 МПа. Для каждого давления (режима) проводилось 5-кратное измерение проницаемости, после чего рассчитывались среднее значение коэффициента проницаемости, а также параметры Δk/k_ср и (k_н-k_к)/k_к, где k_н и k_к - коэффициенты проницаемости при максимальном и минимальном поровом давлении.

Установлено, что коэффициенты проницаемости, полученные на изучаемых образцах, с уменьшением перепада давления значительно возрастают. Так, с уменьшением перепада давления от 0,158 МПа до 0,018 МПа коэффициент проницаемости эталона «Корунд-1» увеличивался на 86,9%. Коэффициент проницаемости эталона «Корунд-2» при уменьшении перепада давления от 0,16 МПа до 0,028 МПа увеличивался на 6,3%. Для образцов горных пород, в составе которых доминирует алевролит, увеличение проницаемости с уменьшением перепада давления выражено в большей степени.

Таблица 1

Результаты определения газопроницаемости

Номер образца	Место-рождение, объект	Литология	Интервал глубин, м	Перепад давления Δp, МПа	Коэффициент проницаемости, мД	Δk/kср, %	(kн-kк)/kк, %
1	-	Эталон «Корунд-1»	-	0,018	2,990	1,10	86,9
				0,055	1,870	0,70
				0,079	1,730	0,50
				0,121	1,688	0,15
				0,158	1,600	0,11
2	-	Эталон «Корунд-2»	-	0,028	5,230	2,80	6,3
				0,045	5,178	1,45
				0,060	5,100	1,40
				0,093	5,078	0,93
				0,127	5,000	0,57
				0,160	4,920	0,60
3	Ковалевская площадь, скв. 4	Алевролит тёмно-серый, кварцевый. Карбонато-метрия: кальцит, доломит	3182,6-3184,2	0,021	0,360	1,20	421
				0,046	0,200	0,90
				0,066	0,118	0,70
				0,115	0,078	0,25
				0,192	0,069	0,20
4	Ковалевская площадь, скв. 4	Алевролит тёмно-серый. Карбонато-метрия: кальцит, доломит	3183,6-3184,2	0,018	0,440	2,50	780
				0,034	0,235	1,80
				0,057	0,163	0,70
				0,072	0,134	0,50
				0,092	0,091	0,40
				0,142	0,062	0,20
				0,198	0,050	0,10
5	Ковалевская площадь, скв. 4	Песчаник тёмно-серый кварцевый. Карбонато-метрия: кальцит, доломит	3180,3-3181,6	0,018	559	2,50	30,9
				0,036	523	1,80
				0,061	486	0,70
				0,097	478	0,50
				0,125	458	0,40
				0,166	427	0,20
6	Месторождение Западной Сибири	Песчаник кварцевый	-	0,050	906,06	4,83	33,1
				0,100	825,52	2,62
				0,150	724,85	1,51
				0,185	680,58	0,35
7	Зареченская площадь, скв. 114	Карбонат	2250-2252	0,029	467	2,30	13,3
				0,048	439	1,90
				0,080	433	0,80
				0,148	420	0,40
				0,168	412	0,20

Как следует из таблицы 1, погрешность определения коэффициента проницаемости эталона «Корунд-1» не превышает 0,11% при перепаде давления около 0,16 МПа. При малых перепадах давления (до 0,03 МПа) максимальная погрешность для эталонов «Корунд-1» и «Корунд-2» составляет 2,8%. Однако не во всём диапазоне давлений в условиях проведения эксперимента погрешность измерения проницаемости столь мала. При перепаде давления ниже 0,004 МПа погрешность может стать значительной и достигает 39,6%. Этот режим можно считать граничным для установления надёжных значений коэффициента проницаемости.

Реакция горных пород на изменение давления не является однотипной. Так, проницаемость образца № 3, которая при ∆p=0,192 МПа равнялась 0,069 мД, при уменьшении перепада давления до 0,021 МПа увеличилась на 421%. Приращение проницаемости образца № 5, которая при ∆p=0,166 МПа равнялась 427 мД, при снижении перепада давления до 0,018 МПа составило всего 30,9%.

На рисунке 1 представлены графики зависимости кажущейся проницаемости от величины, обратной среднему давлению 1/p_ср. Для высокопроницаемых образцов № 5 и № 7 в диапазоне перепадов давлений от 0,02 МПа до приблизительно 0,2 МПа полученные коэффициенты истинной проницаемости k_∞ достаточно близки к значениям, измеренным при перепаде давления около 0,2 МПа (для образца № 7 разница составляет 18%). Коэффициенты проницаемости, рассчитанные по всему диапазону перепада давлений и по интервалу от 0,06 МПа до 0,2 МПа, также практически совпадают. Аналогично для эталона «Корунд-2» при небольшой проницаемости 5 мД коэффициенты проницаемости k_∞ достаточно близки к значениям, измеренным при перепаде давления около 0,2 МПа. Для эталона «Корунд-1» с малой проницаемостью порядка 1мД проницаемость k_∞, рассчитанная в диапазоне перепадов давлений 0,079-0,16 МПа, сопоставима со значением при ∆p=0,16 МПа, однако при снижении перепада давления до 0,02 МПа полученный коэффициент k_∞ существенно отличается от предыдущих значений.

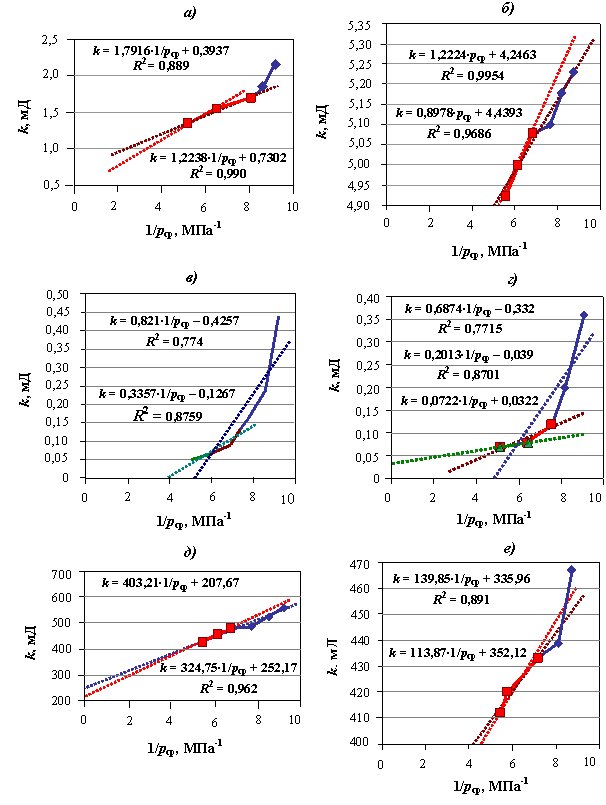
Рис. 1. Графики зависимости проницаемости от 1/p_ср:

а) для образца «Корунд-1»; б) для образца «Корунд-2»; в) для образца № 3;

г) для образца № 4; д) для образца № 5; е) для образца № 7

Для образцов № 3 и № 4 с особо малой проницаемостью горных пород (менее 0,5 мД) точки на графике группируются по нелинейному закону, и по уравнению регрессии нельзя рассчитать k_∞.

В большинстве случаев при использовании в фильтрационных экспериментах воздуха или азота газовая проницаемость горных пород линейно зависит от инверсионного параметра 1/p_ср [8], что эквивалентно соотношению (5). Однако экспериментальные зависимости, полученные в опытах по испытанию слабопроницаемых теплоизолирующих материалов с тонкими капиллярами [6,7], имеют чётко выраженные минимумы и максимумы на участках, которые по теории должны представлять собой практически горизонтальные прямые.

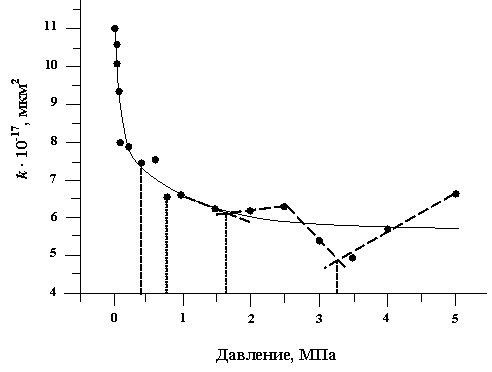
Рис. 2. Преобразованный график зависимости проницаемости

многослойных стеклопластиков от внешнего давления [6,7]

На рисунке 2 в качестве примера показан график зависимости проницаемости многослойных стеклопластиков от давления с четырьмя минимумами – в области внешних давлений 0,4; 0,8; 1,6 и 3,3 МПа. Природу этих минимумов авторы [7] связывают с адсорбцией газа типа многослойной, полагая, что потенциалопределяющие ионы (ПОИ) на внутренней поверхности капиллярно-пористого тела активнее адсорбируют неполярные молекулы воздуха, в основном, азот, по мере увеличения давления. Сила связи проникающих через капилляр молекул с ПОИ при этом увеличивается, число адсорбирующихся молекул возрастает, а проницаемость образцов уменьшается. На рис.2 первый минимум на нисходящей части экспериментальной кривой зависимости проницаемости от давления (≈0,4 МПа) соответствует расчётному давлению, при котором ПОИ полностью заполняются (насыщаются) молекулами воздуха.

Анализируя природу локальных максимумов, фиксируемых на графике зависимости проницаемости от давления, авторы [7] приводят следующие рассуждения. Если между ПОИ и молекулой газа возникает достаточно прочная связь типа ион-индуцированный диполь, то между параллельными индуцированными дипольными моментами адсорбированных молекул возникает диполь-дипольное отталкивание. Это отталкивание передаётся, в том числе, на диполи, расположенные на выходе из капилляра, провоцируя отрыв молекул и значительное увеличение проницаемости. Сила латерального электроповерхностного отталкивания пропорциональна длине капилляра. Авторы [7] вводят понятие равновесной длины капилляра, которая соответствует равенству силы латерального электроповерхностного отталкивания и силы типа ион-индуцированный диполь. Если длина капилляра меньше равновесной, то на выходе из него отрыв молекул, непосредственно адсорбированных на ПОИ, происходить не будет. В этом случае «скольжение» молекул через капилляр будет осуществляться по второму слою, адсорбированному на первом и менее прочно связанному с ПОИ. Отрыв молекул из этого слоя также влечёт за собой увеличение проницаемости.

Авторы [7] не обходят вниманием и то обстоятельство, что, под действием латерального отталкивания и приложенного давления, адсорбированные молекулы с индуцированным дипольным моментом наклоняются к поверхности капилляра. При этом каждый наклонённый индуцированный диполь в образуемом электрическом поле стремится повернуться в направлении, обратном потоку, что препятствует отрыву молекул на выходе из капилляра. Сила обратного отталкивания индуцированных диполей отдельных молекул создаёт давление на макродиполь, которое противодействует внешнему давлению. Это ведёт к дополнительному уменьшению газопроницаемости капилляра при увеличении давления.

Можно предположить, что отклонения от теоретических зависимостей, наблюдаемые в экспериментах по измерению газопроницаемости горных пород, допускают похожее объяснение. Поскольку речь идёт о процессах, протекающих на молекулярном уровне, эффект нарушения линейности связи k-1/p_ср в области малых перепадов давлений отчётливее выражен для низкопроницаемых образцов. В результате снижается точность расчёта истинной проницаемости (по жидкости), которая, как следует из таблицы 2, в несколько раз, а иногда и на порядок отличается от экспериментальных значений.

Таблица 2

Результаты определения проницаемости горных пород по жидкости

№ образца	Месторождение	Интервал, м.м.	№ скв.	Коэффициент проницаемости, мД
				по газу при Δр=0,2 МПа	рассчитан- ный по (5), (9)	по жидкости эксперимен-тально
1	Кочевненское	2350-2370	110	6	5,02	1,14
2	Кочевненское	2376-2383	6	110	103,56	44
3	Дмитриевское	1487-1490	124	3,367	2,71	0,9
4	Дмитриевское	2916-2918	41	0,31	0,19	0,11
5	Дмитриевское	3037-3039	36	590	571,55	104

Измерения коэффициента проницаемости k_∞ образца карбонатной горной породы при увеличении давления обжима до 30 МПа показали закономерное его снижение (таблица 3).

Таблица 3

Зависимость коэффициента газопроницаемости горной породы от

давления обжима образца

Поровое давление, МПа	Коэффициент проницаемости, мД
	Давление обжима, МПа
	4,7	10,7	16,0	21,9	26,2	30,1
0,1	452	421	406	395	380	348
0,15	393	364	369	-	-	-
0,2	374	336	333	317	311	302
0,25	337	310	301	-	-	-
0,3	312	288	279	271	260	235

Таким образом, теория стационарной фильтрации газа в условиях скользящего течения, известные положения которой приведены выше, не позволяет адекватно отразить полученные экспериментальные данные. Очевидно, необходимы дальнейшие исследования в этом направлении. К примеру, в работе [7] предложено различать коэффициенты проницаемости при заряженной и незаряженной поверхности капилляра, а для расчётов характеристик теплозащитных покрытий использовать равновесную проницаемость в предположении равенства силы, продавливающей поток, и силы обратного отталкивания индуцированных диполей молекул (в этом случае поток газа считается стационарным).

Заключение.

Измерения на аппаратуре, позволяющей моделировать пластовые условия при давлении обжима до 31 МПа, показали возрастание проницаемости образцов эталонного корунда, карбонатных и терригенных горных пород по газу в несколько раз в области малых поровых давлений и депрессий. Эффект проскальзывания газа тем больше, чем меньше коэффициент проницаемости пород и перепад давления в образце, однако экспериментальная зависимость газопроницаемости от инверсионного параметра 1/p_ср отклоняется от линейного тренда. Это затрудняет расчёт истинного значения проницаемости по уравнениям регрессии и говорит о том, что ввод константы Клинкенберга в уравнения стационарной фильтрации газа не в полной мере отражает механизм скользящего течения. Для малопроницаемых горных пород в условиях низких перепадов давлений отклонение газопроницаемости от истинных значений может оказаться существенным, что в итоге сказывается на общей оценке фильтрационно-емкостных свойств пластовых систем.

Литература:

1. Klinkenberg L.J. The permeability of porous media to liquids and gases / L.J. Klinkenberg // Am. Petroleum Inst. Drilling and Production Practice, 1941. - PP. 200-211.

2. Методическое руководство по исследованию пород коллекторов нефти и газа физическими и петрографическими методами для производственных лабораторий. - М. ВНИГНИ, 1973.

3. Виноградов В.Г. Практикум по петрофизике / В.Г.Виноградов, А.В.Дахнов, С.Л.Пацевич. - М.: Недра, 1990. – 227 с.

4. Ханин А.А. Петрофизика нефтяных и газовых пластов / А.А.Ханин. - М.: Недра, 1976. – 295 с.

5. Песков А.В. Определение газопроницаемости пород с учётом эффекта скольжения газа / А.В.Песков, В.А.Ольховская // Нефтепромысловое дело. - № 3, 2010. – С. 10-12.

6. Санин А.Ф. Исследование процессов газовой проницаемости композиционных покрытий спускаемых аппаратов / А.Ф.Санин, В.В.Хуторный, С.А.Божко // Вiсник Мiжнародного слов'янського унiверситету. – Харкiв. - Серiя «Технiчнi науки». - Том XI, №1, 2008. - www.nbuv.gov.ua.

7. Плугин А.Н. Механизм воздухопроницаемости теплоизоляционных материалов с тонкими капиллярами / А.Н.Плугин, А.А.Плугин, Т.А.Костюк, Д.А.Бондаренко // Збiрник наукових праць УкрДАЗТ. – Вип.15, 2010. – С. 5-23.

8. Tanikawa W. Klinkenberg effect for gas permeability and its comparison to water permeability for porous sedimentary rocks / W. Tanikawa, T.Shimamoto // Hydrology and Earth System Sciences Discussions, 3, 2006. – P.P. 1315-1338. – www.hydrol-earth-sci-discuss.net/3/1315/2006/