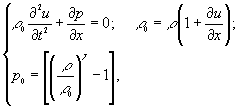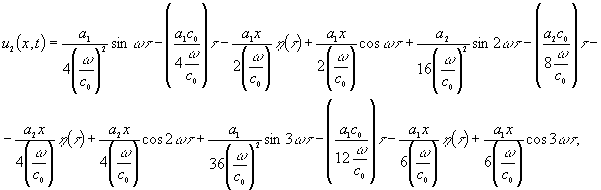Д. т. н., професор Нагорний В.П., к. т. н. Денисюк І.І.

Інститут геофізики ім. С.І. Суботіна НАН України

ДОСЛІДЖЕННЯ ПОШИРЕННЯ АКУСТИЧНИХ ХВИЛЬ В НЕЛІНІЙНИХ СЕРЕДОВИЩАХ

З літературних джерел [1−4] відомо, що з метою підвищення дебіту нафтогазовидобувних свердловин застосовуються акустичні методи дії на геосередовище продуктивних пластів. У більшості розроблених акустичних методів дії на пласт не враховуються нелінійні властивості геосередовищ. Не з’ясований повністю механізм такої дії. У зв’язку з цим представляє науковий та практичний інтерес вивчення механізму розповсюдження акустичних хвиль в нелінійних геосередовищах.

Запишемо основні рівняння одномірного плаского руху в змінних Лагранжа x, t [5]:

(1)

де u(x, t) – зміщення часток середовища зі свого початкового положення x; p, p₀ – змінний та початковий тиск, відповідно; ρ, ρ₀ – змінна та початкова щільність геосередовища, відповідно; γ – показник адіабати Пуассона.

Система рівнянь (1) зводиться до нелінійного рівняння Ірншоу

(2)

де – квадрат рівноважної швидкості звуку.

В нелінійній акустиці мають справу зі слабо нелінійними хвилями, для яких <<1. Вважаючи нелінійність слабкою, рівняння (2) можна звести до наступного:

(3)

Рівняння (3) – це неоднорідне диференціальне рівняння. Ліва частина (3) відповідає звичайному лінійному хвильовому рівнянню, а права частина містить квадратично-нелінійний і кубічно-нелінійний члени.

Покажемо на прикладі простої задачі теорії нелінійних хвиль, а саме поширення гармонічного сигналу з частотою ω в нелінійному геосередовищі, до яких фізичних явищ приводить наявність нелінійних ефектів.

Нехай на межі нелінійного геосередовища (пласт) діє гармонічний сигнал з частотою та амплітудою A. Застосовуючи до нелінійного рівняння (3) метод послідовних наближень, з’ясуємо, які частоти можуть виникати при поширення гармонічного сигналу в нелінійному бездисперсійному геосередовищі.

Вважаючи нелінійні ефекти слабкими, у першому наближенні нехтуємо в рівнянні (3) його правою частиною. Знайдемо розв’язок лінійного хвильового рівняння

(4)

з нульовою початковою і граничною умовами:

; .

(5)

Рівняння (4) з умовами (5) розв’язуємо за допомогою операційного методу. Розв’язок рівняння (4) має вигляд

,

(6)

де .

Щоб знайти розв’язок другого наближення , потрібно підставити вираз (6) в праву частину нелінійного рівняння (3).

Після нескладних математичних операцій одержимо рівняння другого наближення:

(7)

де ; ; .

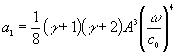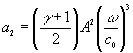Із виразу (7) видно, що має фізичний зміст змушувальної сили у неоднорідному хвильовому рівнянні (7), яка збуджує в геосередовищі нові хвилі за рахунок нелінійних ефектів. Для знаходження виду цих хвиль необхідно розв’язати неоднорідне хвильове рівняння (7).

Рівняння (7) розв’язуємо з використанням операційного методу та методу варіації постійних [6].

В результаті отримаємо розв’язок рівняння (7):

(8)

де – узагальнена одинична функція.

Із аналізу отриманого розв’язку (8) випливає, що при дії на нелінійне середовище гармонічної акустичної хвилі , в ньому за рахунок нелінійних ефектів генеруються хвилі на частотах ω, 2ω і 3ω. Як показують розрахунки, вклад кожної із гармонік у коливальний процес в геосередовищі на відстані x = 1 м від джерела акустичних збурень різний. В таблиці 1, у якості прикладу, приведені максимальні амплітуди коливань часток геосередовища на різних частотах для води та вапняка при x = 1 м; с^-1;  м.

Таблиця 1.

Максимальні амплітуди коливань часток геосередовища на різних частотах при x = 1 м

Геосередовище та його характеристики	Максимальна амплітуда гармонічних коливань часток геосередовищ на різних частотах (у відсотковому відношенні, %)
	ω	2ω	3ω
Вода: γ = 57,15, с0 = 1 500 м/с [7]	16,77	77,72	5,51
Вапняк: γ = 7,55, с0 = 3 500 м/с [7]	8,66	88,54	2,8

Таким чином, основна частина енергії акустичних нелінійних коливань переноситься на круговій частоті 2ω. Особливості генерації хвиль в нелінійних геосередовищах доцільно враховувати при розробці схем та засобів акустичної дії гармонічного виду на продуктивні пласти з метою підвищення їх нафтогазовіддачі.

Література:

1. Горбачев Ю.И. Акустическое воздействие и повышение рентабельности разработки нефтяных месторождений // Каротажник. – 1999. – Вып. 60. – С. 55–67.

2. Свалов А.М. О механизме волнового воздействия на продуктивные пласты // Нефт. хоз-во. – 1996. – № 7. – С. 27–29.

3. Технология акустической реабилитации скважин и пластов для решения задач повышения нефтеотдачи / Э. Орентлихерман, Д. Воронин, А. Исхаков, Ю. Горбачев // Нефть и газ. – 2002. – № 5. – С. 51–55.

4. Афанасенков И.И., Жуйков Е.Ф. Опыт и перспективы промышленного использования акустического воздействия в различных скважинах // Нефт. хоз-во. – 1999. – № 12. – С. 16–19.

5. Зарембо Л.К., Красильников В.А. Введение в нелинейную акустику. – М.: Наук, 1966. – 520 с.

6. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды функции комплексного переменного. – М.: Наука, 1985. – 464 с.

7. Коул Р. Подводные взрывы. – М.: Иностр. лит., 1950. – 495 с.