Технические науки/12. Автоматизированные системы управления на производстве

Cand.Tech.Sci. Belkin E.A.

Orel State Technical University, Russia

Microrelief geometric simulation and technical application

Abstract

A theory for the three dimensional (3D) geometrical model definition of surface layer microrelief on the basis of a modular geometric principle is developed. A device design for the active control of a microrelief formation process the operation principle of which is based on the concept of dynamic holography is also developed. A microrelief formation technique by specified geometrics is developed.

1. Theory

One of the reasons affecting considerably the information completeness of a surface microrelief analytical description is the application of iteration and statistical methods in the ground of which there is no a concept of surface curvature in the local area of the specified point – in the vertex of modulus – of an osculating paraboloid which is estimated by Riemann – Christopher’s tensor.

Thus, the statistical description method of abrasive surfaces with the aid of Markov chain theory allows building only a two dimensional (2D) model including time steps of cutting along an idealized line towards cutting. It does not allow taking into account a cutting edge shape in the direction perpendicular to the vector of a cutting speed and a cutting edge position with respect to successive cutting edges that is essential at the explanation of material removal process.

Thus and so, the development of mathematical modeling methods allowing the replenishment of information shortage in a surface microrelief description occupies a significant place in the shaping theory.

To the main reason which does not allow building a 3D geometrical model strict enough and adequate to a real microrelief one refers the application of the parameter totality of roughness R_a, R_z, R_max and others in one dimensional (1D) microrelief models, and parameters ω_n, ς, γ₀, φ₁, θ₁, Θ₁ in 2D models.

So far there are no sufficiently complete and well substantiated 3D geometrical models of microrelief in the mathematical models of a forming and machined surface. In such a way, for structuring a 3D geometric model of microrelief one should use new scientific approaches.

A modular- geometrical method for a surface microrelief geometric simulation is developed [1].

The theoretical justification of a modular-geometrical method for a microrelief geometric simulation is given. The classification of surfaces with a complex form from the standpoint of geometry cannot have a scientific justification. There are no common signs in the structure of surfaces. A complex form surface is structured on the basis of a modular principle, a structuring method is defined by the problems of a shaping theory. A modular-geometrical method which is used for the solution of these problems consists in the approximation of the local area of a surface with an osculating paraboloid. Riemann – Christoffel’s tensor is a geometric description for the estimate of a local area curvature. The analytical assignment of an osculating paraboloid as a geometric image of the second order of contact with the given local area of a surface is defined from Tailor series expansion. Tailor series also defines geometric images of a higher order of contact: cuboloid, quadroloid and so forth. A surface curvature is estimated in the point of contact through the angle of vector rotation shifted across itself through a closed loop enclosing the point of contact and appertaining to its local area, on the osculating surface: on paraboloid, cuboloid and so forth. The angle of rotation on the surface under consideration depends on vector coordinates:

where Γ^χ_ρσ are the affine connectedness coefficients of the second sort,

indices ν, μ, τ, ω…= 1, 2; d₁x^ν,d₂x^μ - coordinate vector differentials.

This vector is equal to the difference of two vectors obtained as a result of the parallel displacement of the vector ν^χ from the vertex of an infinitesimal parallelogram into an opposite vertex along its sides compiling various parts of a closed loop. It follows that the expressions in square brackets are tensors. Thus,

-

Riemann-Christoffel’s tensor, a considerable component of which is R₁₂₁₂, gives the angle of vector rotation at the parallel displacement through a closed loop on an osculating paraboloid limiting the local area of its vertex. The accuracy order in the definition of covariant differential characterizing changes in vector coordinates does not allow computing a quadroloid curvature. The geometrical structure of cuboloid is not studied. In technical applications one should confine oneself to the approximation of a local area by an osculating paraboloid, as it is possible to postulate in the following way: a surface curvature in the point of contact is equal to the curvature of an osculating paraboloid.

The discrete-defined surface of a work piece in a general case can be approximated through a module set having a smooth “lacing” each of which represents an osculating paraboloid of a certain type.

It is established that a modular approach used for the description of the geometry of framed discrete-defined surfaces at the work piece abrasion may be accepted as a basis for surface microrelief structuring.

At the formation of a simulator describing a surface microrelief one uses a modular principle for structuring a surface with a complex shape and with the solution of problems of uneven “lacing” of separate modules.

On account of the complexity of actually current phenomena the consideration of surface microrelief formation in a work piece is carried out for an ideal model with the following assumptions: environment does not affect a 3D geometrical model of surface microrelief, one can neglect chemical, thermal and dynamic interactions of a tool and a work piece.

There is obtained an analytical presentation for an osculating paraboloid through principle surface curvatures. From equations for the total and mean surface curvature of an osculating paraboloid:

where: K is Gauss or total surface curvature,

H is the mean surface curvature,

k_1, k₂ are the principle surface curvatures,

g₁₁, g₁₂, g₂₂ are the components of a metric tensor,

R₁₂₂₁ is the essential component of Riemann-Christoffel’s tensor (curvature tensor).

From Gauss equation:

R₁₂₂₁ = B₁₁B₂₂,

For the point of contact of the surface under consideration and of an osculating paraboloid in the approximation:

g₁₁g₂₂ – g²₁₂ = 1;

g₁₁ =g₂₂ = 1;

where a given point has coordinates X = 0, Y = 0.

The analytical presentation for the osculating paraboloid:

Z = ½(k₁X² + k₂Y²).

The representation obtained for the osculating paraboloid through the principle surface curvatures, is a significant result on the basis of which there was carried out a numerical computation for the modular geometrical model of surface microrelief.

The system of criteria is established for the quantitative assessment of microrelief topography: k₁, k₂ – the principle surface curvatures, R_z – the microasperity height. The hypothesis substantiated theoretically with respect to the information exhaustiveness of a microrelief topography criterion system is advanced.

The microrelief geometrical model is a body of modules having uneven “lacing” of osculating paraboloids. Each osculating paraboloid can be presented as one of four types pointed out in Tab.1, each type of an osculating paraboloid has a corresponding orientation with respect to Z-axis in XYZ- local coordinate system.

Table 1. Types of an osculating paraboloid

Surface type	Name	Equation presented	Surface kind	В11	В22
I	Elliptic paraboloid		р=1
II	Hyperbolic Paraboloid		р=1
III	Parabolic cylinder		р=1		0
IV	Plane			0	0

where B₁₁, B₂₂ – the coefficients of the second quadratic form.

At the microrelief surface approximation on experimental data the model accuracy testing consisted in the estimate of the maximum error δ_{z max} at the surface conjugation meant for two adjacent design points. The value δ_{z max} was defined as a ratio of a maximum jump on Z-axis at the conjugation of two neighbouring paraboloids to the interval of value changes in experimental data on Z-axis: Z_{ij max} – Z_{ij min} . The performed computations have shown that a surface presentation accuracy depends on the number of design points falling at the interval of a peak or a trough of microrelief.

There is defined a problem for the module factor computation (Tab. 2) of surface microrelief, in a general case: a surface is decomposed through a chosen pitch on Z-axis of Cartesian coordinate system by planes parallel to XY-plane and one-parameter family of surfaces. A subinterval of a family of surfaces is set with respect to a family parameter. The nodes of microrelief and the families of parallel planes and surfaces are defined. A module - surface local area – as a part of the surface of an osculating paraboloid is rebuilt through five points. The problem solution for a module factor computation in a particular case for the flat of a part [2] consists in the following:

Table 2. The module type definition of the three-dimensional geometrical model (TGM) of microrelief

№	TGM module type	Factor sign
1.	k1X^2+k2Y^2≥-2Z;	k1>0; k2>0;
2.	k1X^2+k2Y^2≤-2Z;	k1<0; k2<0;
3.	k1X^2+k2Y^2≤ 2Z;	k1>0; k2<0; (k1<0, k2 >0);
4.	k2Y^2≥-2Z	k1=0; k2>0; (k1=0, k2<0);
5.	Z≤0;	k1=0; k2=0.

In the global system of Cartesian rectangular coordinate system there is set a point field definable with values n on X-axis and values m on Y-axis.

For each point (x_i,y_j), ; there is known a value z_ij (Fig. 1, 2).

A subinterval on x-axis is Δx= (x_n-x₁)/n. A subinterval on y-axis is Δy= (y_m-y₁)/m.

In the node – (x_i+l; y_j; z_k+1) on the basic area L_x x L_y,

where

1≤i≤n_x +1, 1≤ j≤ n_y + 1, 1≤ k ≤ (1 + n_x)(1 + n_y);

one defines radii of curvature R_l1, R_l2 through three points in the sections x_i+1; y_j; through the nodes of microrelief real profiles (Fig. 3, 4)

On the basis of Meunsnier theorem the normal curvatures are calculated in the sections x_i+1; y_j;:

where φ₁ and φ₂ are the angles between the principle normal of paraboloid and circular arc normals in the sections x_i+1; y_j.

Supposing that a normal curvature in one of the sections is equal to the principle curvature k₁ = k_ln, through Dupin indicatrix one defines the principle curvature k₂ in the section perpendicular to the section chosen (Fig. 5, 6).

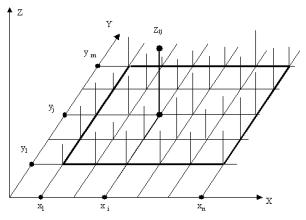
Fig. 1. The model of microrelief decomposition Fig. 2 . Basic data for the computation

by interperpendecular planes of microrelief

Fig. 3. Microrelief decomposition in Fig. 4. The scheme to the computation

the plane y = y_i of the curvature radius in the section

of y = y_i

Fig. 5. The XYZ – coordinate system Fig. 6. The modular geometrical model

in the point of contact of surface microrelief 30x6 mcm of a sample

after flat grinding:(scanning pitch 0.001mcm)

Through the values k₁ and k₂ the type of module for a geometrical model in Cartesian local rectangular coordinate system with the beginning in the node –(x_i+1; y_j) is defined. The procedures for the numerical computation are developed for the microrelief of surfaces (flat, circular cylindrical, framed discrete-defined and solids of irregular form) [3].

2. Inspection tools for control of microrelief formation process

Modern inspection tools are designed in such a way that recorders register the values of parameters from the outline maps of an object. The outline maps are defined either with low accuracy, or in the course of a rather long period of time. It is impossible to carry out control of an out-of-the-way object – abrasive grains moving in work piece material.

There is one method among the ways for the enhancement of inspection tool capabilities and the use of information obtained with their assistance for the creation of three dimensional models, the application of devices investigating an object holographic display.

The control principle of tools under consideration is based on the latest researches of the processes of obtaining an object holographic display in optical and X-ray (roentgen) bands. The devices in this line allow studying manufacturing processes not in a plane projection, but in space.

3. Roentgenoprofilograph of active control

The problem, for the solution of which is used the device offered, consists in the provision of possibility to carry out control of a microgeometry formation in a surface layer of a work piece in the course of abrasion and to research the mechanism of processes accompanying a microrelief formation: chip removal, abrasive grain spalling and extraction of abrasive grains from the set of tools, grain microoscillation appearance in the tool set, changes in porous structure of a tool set, microchip formation, a plastic shift and strengthening material to be machined with single grain and grain aggregate and so forth.

It is achieved by that in a roentgenoprofilograph of active control [4] having X-ray emitter, a crystal resonator for obtaining monochromatic X-ray emission, focusing crystal systems –collimators, the principle of operation of one of them is based on eight-beam diffraction, crystal mirrors for the separation and change of X-ray emission propagation direction, recording environment – crystal – analyzer for obtaining wave interference, the increase of a three dimensional interference image is carried out with the aid of a reflecting microscope at the recording of a holographic display of the object under research, and for measuring one uses a three dimensional matrix compiled of electron-optical image intensifiers.

4. Means for microrelief formation

The procedure for the prediction of new ways of machining is based on the theoretical researches of a three dimensional geometrical model of a work piece surface and consists in that a binary correspondence of a forming surface is established on the basis of the developed allocation for a work piece surface. Under this correspondence the prediction of new ways of shaping is carried out.

The work piece surface is represented as a superposition of a three dimensional geometrical model with module smooth “lacing” which gives the idea of geometry in whole and a model with module uneven “lacing” which contains the information of forming surface microrelief .

Types of machining are defined.

The first type: ways allowing reproducing forming surface geometry theoretically correct. In their basis there is a modification of the contact mode of a tool and a part blank. The way of grinding the blade wing of a gas turbine with the aid of profilecomposite tools belongs to the first type. [5]

The second type: ways permitting the representation of work piece surface microrelief in accordance with given geometrical data. Changes in the procedure of machining allowance removal are in their basis. The grinding way with the use of an elbore tool with a metallic fiber set belongs to the second type. [6]

The third type: ways allowing reproducing the geometry of work piece surface and its microrelief theoretically correct and in accordance with the given geometrical data. Tool microgeometry changes in the course of a work piece machining are in their basis. The way of gas turbine blade wing grinding with a flexible bundle in a magnetic field belongs to the third type. [7]

For the realization of the predictable way of microrelief formation allowing producing its microgeometry according to the given geometrical data the optional equipment – counterpart (prototype) of a cyclotron – an elementary particle accelerator is required.

Abrasive particles existing in a magnetic field are used as a tool. The analytical assignment of a part surface: a gas turbine blade wing is used for the computation of the general homohelical path of abrasive particle motion. To the charged abrasive particles controlled by a magnetic field pertaining to a blade wing is imparted a motion by a general homohelical path in accordance with the type of blade, changes of a helical path of abrasive particles and the substitution of an abrasive particle fraction.

5. Blade wing grinding method for gas turbine by flexible tool set in magnetic field

The problems, which the invention is aimed at, consist in combining in one production cycle the main abrasion operations of a blade wing in a gas turbine beginning from roughing and up to finishing in one technological system, in widening the type spectrum of work blades, shaping accuracy increase in macrogeometry of a blade wing and at the control on the given data: an abrasion depth, a temperature field and a curvature tensor and so forth, surface layer microshaping.

The problems put by should be solved by the offered method of grinding through which in a resonance accelerator – cyclotron to the charged abrasive particles controlled by a magnetic field one imparts, relative to a part, a motion along a general homohelical path on the basis of conditions securing favourable changes in a general homohelical shaping surface in accordance with a blade type, changes in the kind of an abrasive particle helical path in accordance with the given shaping surface, and a possibility of the fraction substitution of abrasive grains.

In this connection, before surface machining (entrance and exit edges, back, tray) one describes gas turbine blades in an analytical way on the basis of the modular geometrical model of a surface with a complex shape, the obtained analytical assignment of a blade wing is used for the computation of a general homohelical path of abrasive particles.

Conclusions:

1. The method for the definition of microrelief topography is developed which allows building a three dimensional geometrical model of microrelief on the basis of experimental data.

2. A possibility for the substantiation of the prediction of tool development for passive and active nondestructive control allowing carrying out estimations on the basis of three dimensional geometrical models is given.

3. The prognostics in the development of devices for passive and active nondestructive control of a microrelief formation process is carried out, the control principle of which is based on the latest researches of processes in obtaining a holographic image of objects in optical and roentgen bands.

4. The substantiation for the possibility of forecasting new machining methods allowing microrelief forming by given geometric data is presented.

5. The recommendations for forecasting the method for a microrelief formation allowing the representation of its microgeometry by given geometric data, abrasion methods of a blade wing for a gas turbine in a flexible bundle in a magnetic field are given.

References

[1] Y.S. Stepanov, E.A. Belkin, G.V. Barsukov, ”Simulation of abrasive tool microrelief and part surface”, Monograph, M.:, Publishing House “Mashinostroyenie-1”, 2004, pp. 215, Patent RF № 2229970, Method for manufacturing elbore abrasive tool in metal fiber bundle/ Y.S. Stepanov, E.A. Belkin, G.V. Barsukov, Patent application 29.07.2002, published 10.06.2004, Bulletin № 16.

[2] Patent RF № 2187070, “Method for part and abrasive tool surface microgeometry definition” / Y.S. Stepanov, E.A. Belkin, G.V. Barsukov, Patent application 27.02.2001, published 10.08.2002, Bulletin № 22.

[3] Certificate № 2008612886, Software “CAD-Grinding”, E.A. Belkin, Patent application 25.12.2007, registered 11.06.2008.

[4] Patent FR № 280204, “Roentgenprofilograph for active control”/ E.A. Belkin, Patent application 24.10.2005, published 12.02.2007, Bulletin № 22

[5] Patent RF № 2217290, “Method for blade wing grinding by profilecomposite tools for gas turbine” / Y.S. Stepanov, E.A. Belkin, G.V. Barsukov, Patent application 26.03.2002, published 27.11.2003, Bulletin № 33

[6] Patent RF № 2229970, “Method for manufacturing elbore abrasive tool in metal fiber bundle”, / Y.S. Stepanov, E.A. Belkin, G.V. Barsukov, Patent application 29.07.2002, published 10.06.2004, Bulletin № 16

[7] Patent RF № 2266188, “Method for blade wing grinding of gas turbine by tools with flexible bundle in magnetic field”, / E.A. Belkin, Patent application 22.03.2004, published 20.12.2005, Bulletin № 35.