3D-МОДЕЛИРОВАНИЕ КИНЕМАТИЧЕСКИХ ПРОЦЕССОВ МАНИПУЛЯТОРОВ

Л.Т. Раевская, А.В. Швец, Ф.Ф. Дахиев

Уральский государственный лесотехнический университет г.Екатеринбург РФ

При эксплуатации машин манипуляторного типа в лесной отрасли динамические процессы, происходящие в механизмах и агрегатах лесных машин, приводят к появлению неполадок, снижению срока службы, уменьшению времени наработки на отказ. Эксплуатационные характеристики существенным образом зависят от вибрационных процессов и колебаний манипулятора при перемещении груза. Особый случай возникает при перемещении хлыста со смещенным центром тяжести хлыста относительно точки захвата манипулятора. В качестве начала исследования процессов колебаний нам представляется важным исследовать кинематику отдельных звеньев манипулятора в пространственном случае. На стадии проектирования важную роль играет учет ускорений отдельных звеньев и груза и их влияние на динамические составляющие. Зная, например, ускорения отдельных точек и звеньев манипулятора, можно определить инерционные добавки: силы инерции и моменты сил инерции и оценить динамические нагрузки. При этом проектируемый манипулятор должен обладать следующими свойствами: высокой надежностью, малым общим весом, «достаточной рабочей зоной и хорошими траекториями движений элементов манипулятора» [1] и т.д.

В настоящей работе поставлена задача определения линейных и угловых характеристик точек и звеньев манипулятора в зависимости от времени для пространственного движения. Переход от технического объекта к расчетной схеме изображен на рис. 1, где не показаны гидроцилиндры, стойка и другие, незначительные для исследования кинематики звенья.

Составим уравнение векторного контура ОAB (рис. 1).

, (1)

где – радиус-вектор точки подвеса груза. Положение звеньев в пространстве задается угловыми координатами , , . Угловые

Рис.1. Расчетная схема манипуляторного механизма

координаты откладываются от оси Х и линии ОВ´ в направлении против хода часовой стрелки. Координаты точки В – , , (рис. 1) – являются основными координатами, так как через эти координаты можно определить главные геометрические параметры рабочего процесса перемещения точки B. На расчетной схеме т. О – точка крепления стрелы к стойке – выбрана за начало отсчета. Дифференцируя проекции уравнения (1) на координатные оси по времени t (при условии ), получим дифференциальные уравнения, из которых можно вычислить функции скоростей механизма:

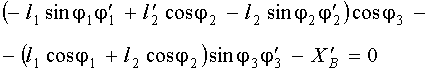(2)

(3)

(4)

В систему уравнений (3)-(5) входят 7 неизвестных параметров – функции скоростей механизма – , , , , , , . Для того, чтобы система была замкнута, необходимо составить еще четыре уравнения. Недостающие уравнения составляют для каждого конкретного случая либо задавая зависимости от времени для скорости точки В и длины рукояти, либо для углов поворота и длины рукояти.

Для расчета угловых скоростей запишем уравнения (2)-(4) в виде удобном для решения по правилу Крамера:

(5)

Из системы (5) по известным формулам через соответствующие определители получаем соотношения для угловых скоростей

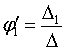, , . (6)

Дифференцируя соотношения (5) по времени получаем выражения для угловых ускорений. Например, для углового ускорения стрелы манипулятора найдено следующее соотношение

(7)

В соотношении (7) введены обозначения а_р-ускорение выдвижения телескопической рукояти, а_х, а_у, а_z - ускорения, а V_x, V_y, V_z –cкорости точки захвата груза относительно координатных осей, ω₁, ω₂ , ω₃ – угловые скорости соответствующих звеньев манипулятора. Зная угловые ускорения можно оценить главный вектор момента сил инерции, дающий вклад в динамические нагрузки.

Библиографический список

1. Герасимов Ю.Ю. Проектирование и расчет манипуляторов лесных машин/ Ю.Ю.Герасимов, В.С. Сюнев, А.П. Соколов, С.А. Кильпеляйнен. Учеб. пособие. –Петрозаводск: Изд-во ПетрГУ, 2006.-92 с.