Технические науки/4. Транспорт
Д.т.н.,
проф. Тарасов В.Н., к.т.н., доцент Бояркина И.В.
Сибирская
государственная автомобильно-дорожная академия
(СибАДИ), Россия
ТЕОРЕМА ВЫСОТ ТРЕУГОЛЬНИКА В МАТЕМАТИКЕ
И ТЕХНИКЕ
Аннотация. В статье рассмотрены теоремы, связанные с решениями
треугольников в геодезии, строительстве, машиностроении. Для определения высот
треугольника предложена теорема, которая по сравнению с известными формулами в
математике является наиболее простой. Простота теоремы обеспечена
использованием параметров одной вершины треугольника. В статье приводится
пример решения кинематических треугольников гидромеханизмов с ведущим поршнем.
Ключевые
слова: теорема, треугольник,
алгоритм, высота треугольника, вершина, геодезия, строительство, машиностроение,
гидромеханизмы с ведущим поршнем
Теорема – это утверждение, истинность
которого устанавливается с помощью бесспорных доказательств, аксиом, раннее
доказанных теорем [1].
Одной из таких теорем в геометрии является
теорема Пифагора, которая будучи одной из первых теорем геометрии является
некоторым геометрическим законом. Именно Пифагор придал этому закону статус
теоремы и обратил внимание ученых на его важность не только для геометрии, но и
всей науки [2].
Геометрическая сущность этой теоремы могла
быть осмыслена и окончательно утвердилась в сознании людей в 6 веке до нашей
эры только после установления единицы измерения площади поверхности и понятий
площадей плоских фигур квадрата и прямоугольника.
Площадь фигуры квадрата, построенного на
гипотенузе прямоугольного треугольника, равна сумме площадей двух плоских фигур
– квадратов, построенных на катетах этого треугольника. В течение тысячелетий
новые поколения людей убеждаются в правильности алгоритма этой теоремы.
Дальнейшее развитие геометрии в течение
последних тысячелетий увенчалось созданием фундаментальных теорем, многие из
которых в той или иной мере использовали теорему Пифагора [3]. Эта теорема явилась
толчком для развития алгебры.
Плоский треугольник является простейшей
фигурой, с помощью которой создаются
другие более сложные фигуры как плоские, так и пространственные.
Появление компьютеров и компьютерных
технологий позволяет решать сложные задачи, которые предъявляют новые
требования к существующему фундаменту современной науки.
Современные теоремы геометрии
сформулированы для треугольников с постоянными размерами сторон  , b, с. Однако,
наряду с этим классом задач для треугольников существует другая группа задач
кинематики, в которых одна сторона треугольника является переменной функцией, а
две другие – постоянные величины. Существуют более сложные классы задач,
связанных с треугольниками, в которых две или все три стороны треугольника
являются переменными величинами. Для таких задач в математике отсутствуют
какие-либо теоремы. Обращает на себя внимание отсутствие в математике теорем,
посвященных высоте вершин треугольника [2, 3].
, b, с. Однако,
наряду с этим классом задач для треугольников существует другая группа задач
кинематики, в которых одна сторона треугольника является переменной функцией, а
две другие – постоянные величины. Существуют более сложные классы задач,
связанных с треугольниками, в которых две или все три стороны треугольника
являются переменными величинами. Для таких задач в математике отсутствуют
какие-либо теоремы. Обращает на себя внимание отсутствие в математике теорем,
посвященных высоте вершин треугольника [2, 3].
Высоты 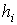 треугольника являются
важными геометрическими характеристиками наряду с медианами, биссектрисами,
радиусами R и r и
т.д. В математике известны формулы для определения высот треугольника через его
стороны
треугольника являются
важными геометрическими характеристиками наряду с медианами, биссектрисами,
радиусами R и r и
т.д. В математике известны формулы для определения высот треугольника через его
стороны  , b, c, использующие функцию синуса и формулы полупериметра
[3]. В геодезии для определения одной высоты треугольника с помощью теоремы
Пифагора используются две формулы–близнецы, полученные из левого и правого прямоугольных
треугольников, прилежащих к высоте [4, 5, 6]. Записи указанных формул в
конечном виде не приводятся в указанных источниках по причине отсутствия
единого простого алгоритма для их определения.
, b, c, использующие функцию синуса и формулы полупериметра
[3]. В геодезии для определения одной высоты треугольника с помощью теоремы
Пифагора используются две формулы–близнецы, полученные из левого и правого прямоугольных
треугольников, прилежащих к высоте [4, 5, 6]. Записи указанных формул в
конечном виде не приводятся в указанных источниках по причине отсутствия
единого простого алгоритма для их определения.
В современных машинах широкое применение
получили рычажные механизмы, в которых возникают кинематические треугольники, содержащее звено переменной длины с ведущим поршнем [7]. Авторами статьи
получена теорема высот вершин треугольника, позволяющая определять высоты вершин
любого треугольника через стороны 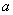 , b , c для всех вершин по алгоритму: квадрат высоты вершины треугольника равен разности квадратов гипотенузы
и катета, при этом гипотенуза есть произведение двух сторон, образующих
вершину, поделенное на основание; катет содержит сумму квадратов двух сторон,
образующих эту вершину, минус квадрат основания, поделенные на удвоенное основание.
, b , c для всех вершин по алгоритму: квадрат высоты вершины треугольника равен разности квадратов гипотенузы
и катета, при этом гипотенуза есть произведение двух сторон, образующих
вершину, поделенное на основание; катет содержит сумму квадратов двух сторон,
образующих эту вершину, минус квадрат основания, поделенные на удвоенное основание.
Для вершины, имеющей, например, угол А (рис.
1), которому соответствует основание 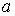 треугольника, квадрат
высоты
треугольника, квадрат
высоты 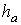 согласно теореме
имеет
согласно теореме
имеет
вид.
 . (1)
. (1)
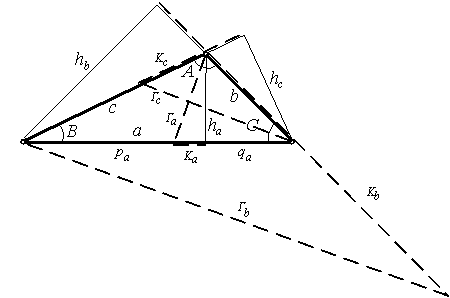
Рис.
1. Схема треугольника к определению высот 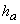 ,
,  ,
, 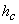
Сущность теоремы заключается в том, что
для любого треугольника квадрат высоты вершины треугольника определяется как
разность квадратов гипотенузы и катета.
Для вершины с углом А можно записать
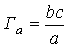 ;
; 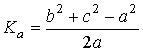 , (2)
, (2)
где  ,
, 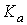 – соответственно
гипотенуза и катет для вершины А.
– соответственно
гипотенуза и катет для вершины А.
Квадрат высоты треугольника для вершины А по теореме Пифагора имеет вид

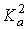 . (3)
. (3)
На рис. 1 показаны гипотенузы и катеты для
всех вершин треугольника.
Для сравнения теоремы (1) с известными формулами
высот треугольника отметим некоторые очевидные факты.
Запишем формулы-близнецы высоты 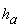 треугольника для
правого и левого прямоугольных треугольников, используя рис. 1 и теорему
Пифагора
треугольника для
правого и левого прямоугольных треугольников, используя рис. 1 и теорему
Пифагора
 ; (4)
; (4)
 , (5)
, (5)
где 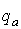 ,
, 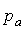 – проекции сторон треугольника
на основание.
– проекции сторон треугольника
на основание.
Катет  определяется по формуле
определяется по формуле
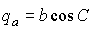 , (6)
, (6)
где 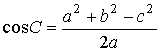 . (7)
. (7)
Аналогично вычисляется катет  .
.
Таким образом, из формул (4), (5)
получаются известные формулы-близнецы для определения одной высоты треугольника
 ; (8)
; (8)
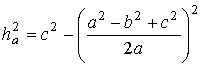 . (9)
. (9)
Приведенные формулы (4), (5), (6), (7)
являются алгоритмом для вывода известных формул (8), (9). Сложность алгоритма
вычисления высоты заключается в использовании параметров трех вершин
треугольника. Алгоритм получения известных формул (8), (9) начинается с
привязки высоты 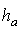 к вершине треугольника,
например, А (см. рис. 1), которую
образуют стороны b, c. При этом
нужно выбрать или правую или левую гипотенузу, т.е. b или c.
к вершине треугольника,
например, А (см. рис. 1), которую
образуют стороны b, c. При этом
нужно выбрать или правую или левую гипотенузу, т.е. b или c.
Вторая часть формул (8), (9) связана с
другими вершинами С или В, которые тоже нужно выбирать. Разные
по внутреннему содержанию формулы (8), (9) по существу являются
формулами-близнецами, т. к. определяют одну величину  . Эти формулы используются для записи теоремы синусов.
. Эти формулы используются для записи теоремы синусов.
Следует отметить, что запись формул (8), (9)
происходит для принятой системы обозначения сторон и углов треугольника. В
прикладных задачах обычно используют другие обозначения сторон треугольника, отличные
от обозначений на рис. 1, поэтому пользователям теорем приходится всегда делать
вывод этих формул заново и только после этого выполнять расчеты. В этой ситуации
главную роль играют алгоритмы записи формул высот треугольника и предпочтение
отдается более простым алгоритмам, имеющим геометрическое смысловое содержание.
В теореме (1) гипотенуза и катет, например 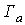 и
и  заменяют катеты
заменяют катеты 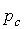 и
и  в формулах (8), (9)
(см. рис. 1), при этом все операции алгоритма привязаны к одной вершине А. Выполним самое простое доказательство
теоремы высот треугольника. При помощи рис.1 определим площадь треугольника
двумя способами: используя высоту
в формулах (8), (9)
(см. рис. 1), при этом все операции алгоритма привязаны к одной вершине А. Выполним самое простое доказательство
теоремы высот треугольника. При помощи рис.1 определим площадь треугольника
двумя способами: используя высоту  и основание b треугольника, и используя высоту
и основание b треугольника, и используя высоту  и основание a
треугольника
и основание a
треугольника
 . (10)
. (10)
Используя (10), определим высоту
треугольника
 . (11)
. (11)
Возведем в квадрат левую и правую части
уравнения (11) и заменим квадрат синуса, квадратом косинуса
 . (12)
. (12)
Выразим 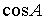 из теоремы косинусов
из теоремы косинусов
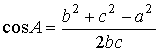 . (13)
. (13)
Подставляя (13) в (12) получаем окончательно теорему (1).
На основе рассмотренных результатов
выполним обобщение рассматриваемой проблемы.
Используя понятие тригонометрических
функций непосредственно из рис. 1 запишем формулы площади треугольника,
помещенные в первой строке таблицы.
Таблица
Из этих формул определим высоты
треугольника для соответствующих вершин А,
В, С, помещенные во второй строке таблицы.
В третьей и четвертой строках помещены
формулы-близнецы для вычисления высот треугольника. И, наконец, пятая строка
содержит конечные формулы теоремы для вычисления высот треугольника, полученные
из формул второй строки. Обращаем внимание на то, что в математике отсутствуют
формулы пятой строки таблицы, которые являются более удобными для практического
пользования и являются теоремой.
На рис. 2 представлена кинематическая
схема рабочего оборудования фронтального погрузчика, содержащая гидромеханизмы
подъема стрелы и поворота ковша.

Рис.
2. Расчетная схема механизмов рабочего оборудования фронтального погрузчика:
1- портал; 2 –
стрела; 3- рычаг; 4 – тяга; 5 – ковш; 6 – гидроцилиндр стрелы;
7
- гидроцилиндр ковша; 8 – передний мост погрузчика
Гидроцилиндр 6 подъема стрелы 2 рассматривается как звено переменной длины  . Гидроцилиндр 7 поворота ковша – звено переменной длины
. Гидроцилиндр 7 поворота ковша – звено переменной длины  . Звенья кинематической схемы на рис. 2 образуют четыре
кинематических треугольника с вершинами:
. Звенья кинематической схемы на рис. 2 образуют четыре
кинематических треугольника с вершинами:  ;
;  ;
;  ;
; 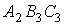 . В указанных треугольниках две или одна стороны являются
постоянными величинами.
. В указанных треугольниках две или одна стороны являются
постоянными величинами.
Важнейшим кинематическим параметром
представленных механизмов являются плечи силовых звеньев: 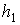 – плечо силового
звена гидроцилиндра стрелы;
– плечо силового
звена гидроцилиндра стрелы;  – плечо силового
плеча гидроцилиндра рычага;
– плечо силового
плеча гидроцилиндра рычага; 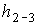 – плечо тяги;
– плечо тяги;  – плечо ковша.
Указанные плечи удобно вычислять по формулам высот треугольника. Например, для
вершины
– плечо ковша.
Указанные плечи удобно вычислять по формулам высот треугольника. Например, для
вершины 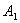 высота
высота 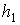 определяется из
треугольника
определяется из
треугольника  по теореме
по теореме
 .
(14)
.
(14)
Достоинством разработанной теоремы
является простота алгоритма, позволяющего определять высоты вершин треугольника,
не используя формулу полупериметра, не привлекая другие теоремы, например,
синуса или косинуса для предварительного вычисления углов. Простота алгоритма
теоремы обеспечивается использованием параметров одной вершины треугольника при
вычислении высоты.
В результате использования теоремы высот
треугольника повышается надежность вычислений, связанных с расчетами
треугольников в космонавтике, геодезии, строительстве, машиностроении и других
областях деятельности людей.
Вывод
При расчетах, связанных с треугольниками,
теорема высот треугольника является полезной наряду с теоремой Пифагора,
теоремами синусов и косинусов.
Литература
1. Большая энциклопедия в шестидесяти двух
томах: том 50.-М.: Терра, 2006.-592 с.
2. Выгодский М.Я. Справочник по
элементарной математике.- М.: Издательство «Наука», 1964.-420 с.
3. Корн Г., Корн Т. Справочник по
математике для научных работников и инженеров.-М.: Издательство. Наука. Гл.
ред. физ.-мат. лит., 1974.-832 с.
4. Полевой В.А. Математическая обработка
результатов радиогеодезических измерений.- М.: Изд-во «Недра», 1971.-342 с.
5. Поклад Г.Г. Геодезия: учебное пособие
для вузов.-М.: Академический Проект, 2008.-590 с.
6. Клюшин Е.Б. и др. Инженерная геодезия:
учебник для студентов высших учебных заведений под ред. Д.Ш. Михелева.- М.:
Издательский центр «Академия», 2006.-474 с.
7. Тарасов В.Н., Бояркина И.В., Коваленко
М.В., Федорченко Н.П., Фисенко Н.И. Теоретическая механика.- М.: Изд-во
ТрансЛит,2010.-560 с.
![]() , b, с. Однако,
наряду с этим классом задач для треугольников существует другая группа задач
кинематики, в которых одна сторона треугольника является переменной функцией, а
две другие – постоянные величины. Существуют более сложные классы задач,
связанных с треугольниками, в которых две или все три стороны треугольника
являются переменными величинами. Для таких задач в математике отсутствуют
какие-либо теоремы. Обращает на себя внимание отсутствие в математике теорем,
посвященных высоте вершин треугольника [2, 3].
, b, с. Однако,
наряду с этим классом задач для треугольников существует другая группа задач
кинематики, в которых одна сторона треугольника является переменной функцией, а
две другие – постоянные величины. Существуют более сложные классы задач,
связанных с треугольниками, в которых две или все три стороны треугольника
являются переменными величинами. Для таких задач в математике отсутствуют
какие-либо теоремы. Обращает на себя внимание отсутствие в математике теорем,
посвященных высоте вершин треугольника [2, 3]. ![]() треугольника являются
важными геометрическими характеристиками наряду с медианами, биссектрисами,
радиусами R и r и
т.д. В математике известны формулы для определения высот треугольника через его
стороны
треугольника являются
важными геометрическими характеристиками наряду с медианами, биссектрисами,
радиусами R и r и
т.д. В математике известны формулы для определения высот треугольника через его
стороны ![]() , b, c, использующие функцию синуса и формулы полупериметра
[3]. В геодезии для определения одной высоты треугольника с помощью теоремы
Пифагора используются две формулы–близнецы, полученные из левого и правого прямоугольных
треугольников, прилежащих к высоте [4, 5, 6]. Записи указанных формул в
конечном виде не приводятся в указанных источниках по причине отсутствия
единого простого алгоритма для их определения.
, b, c, использующие функцию синуса и формулы полупериметра
[3]. В геодезии для определения одной высоты треугольника с помощью теоремы
Пифагора используются две формулы–близнецы, полученные из левого и правого прямоугольных
треугольников, прилежащих к высоте [4, 5, 6]. Записи указанных формул в
конечном виде не приводятся в указанных источниках по причине отсутствия
единого простого алгоритма для их определения.![]() , b , c для всех вершин по алгоритму: квадрат высоты вершины треугольника равен разности квадратов гипотенузы
и катета, при этом гипотенуза есть произведение двух сторон, образующих
вершину, поделенное на основание; катет содержит сумму квадратов двух сторон,
образующих эту вершину, минус квадрат основания, поделенные на удвоенное основание.
, b , c для всех вершин по алгоритму: квадрат высоты вершины треугольника равен разности квадратов гипотенузы
и катета, при этом гипотенуза есть произведение двух сторон, образующих
вершину, поделенное на основание; катет содержит сумму квадратов двух сторон,
образующих эту вершину, минус квадрат основания, поделенные на удвоенное основание.
![]() треугольника, квадрат
высоты
треугольника, квадрат
высоты ![]() согласно теореме
имеет
согласно теореме
имеет  .
.
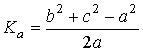 ,
,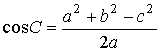 .
. ;
;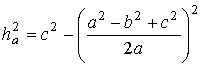 .
. .
.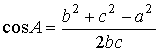 .
.
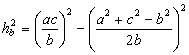
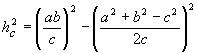

 .
.