К. т. н., Бондаренко Л. Н., Бондарева О. А.

Днепропетровский национальный университет железнодорожного транспорта имени академика В. Лазаряна

ОПРЕДЕЛЕНИЕ КОНЕЧНОЙ СКОРОСТИ ПРИ КАЧЕНИИ
ПО ЛОМАНОЙ ПРЯМОЙ

Предлагаемая задача рассмотрена ещё Галилеем, который установил время движения тела по наклонной плоскости под действием силы тяжести. Было установлено, что это время относится к длине пути, как время падения с той же высоты.

Без учёта сопротивления трению качению этот закон легко выводится из закона свободного падения с применением правила разложения сил.

Очевидно, что общее время скатывания вагона по ломаной (рис. 1)

,

где ; , которое будет меньшим времени без учета сопротивления качению, .

Рис. 1 Расчетная схема

Отсюда делается важное заключение: хотя прямая и является кратчайшим расстоянием между и , но не она является линией «наименьшего времени».

С учётом сопротивления качению, например колеса по рельсу, эта задача не решалась ранее ввиду отсутствия аналитической зависимости, а именно её основной составляющей – коэффициента трения качения.

В задаче о движении колесного ската, наведенной в известном учебнике по теоретической механике [1], утверждается, что коэффициент трения качения не зависит от величины реакции, но имеет различные значения для разных материалов и для стальных бандажа и рельса рекомендуется = 0,05 см.

Очевидно, автору не были известны опубликованные примерно в это же время, исследования Табора [2], посвящённые аналитическому определению коэффициента трения качения, но наличие в этих формулах коэффициента гистерезисных потерь свели на нет их практическое применение.

В [3] предложены формулы, не содержащие его и имеющие следующий вид:

при первоначальном линейном контакте

; (1)

при первоначальном точечном контакте

, (2)

где – полуширина статического пятна контакта; – радиус тела качения в метрах.

Отметим, что коэффициент гистерезисных потерь в формулах Табора довольно точно описывается экспонентой в формулах (1) и (2).

Цель исследований – найти сопротивление качению колеса по рельсу и от трения роликов в буксах с учётом уклона пути и уточнить необходимую длину сортировочной горки.

Основной материал исследований – полуширина пятна контакта между колесом и рельсом при давлении колеса на рельс , радиусе головки рельса и радиусе колеса [4]

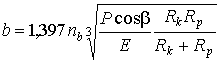, (3)

где – коэффициент, зависящий от отношения коэффициентов уравнения эллипса касания; здесь принято, что модули упругости материалов колеса и рельса одинаковы, а коэффициент Пуассона равен 0,3.

Например, при нагрузке на колесо = 105 кН; = 2,1∙10⁵ МПа;
= 1000 МПа радиус колеса =525 мм. При этих данных = 5,5 мм; = 1,25 мм сопротивление качению колеса составит =2000 Н.

Найдём сопротивление в буксах при подшипниках букс 2Н32732Г. Для этого приведём, не обращая внимания на величину контактных напряжений, всю нагрузку, приходящуюся на подшипник, к одному ролику. Это, как доказано в [5], справедливо при нагрузке на группу тел качения, изменяющейся примерно по синусоидальному закону.

Статическая полуширина пятна контакта условного ролика с внутренней беговой дорожкой

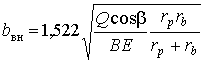, (4)

где – нагрузка на один подшипник; , – радиусы ролика и внутренней дорожки катания; – длина ролика. Между нагруженной дорожкой и роликом полуширина пятна

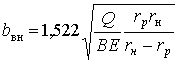. (5)

Коэффициент трения качения соответственно составит:

; (6)

. (7)

Сопротивление одного подшипника, приведенное к радиусу катания колеса:

.

При =52,5 кН; =99 мм; получим =21 мм; =0,393; ; ; ; Н.

Если вагон пустой, то =0,2; мм; ; мм; Н.

Полное сопротивление движению гружёного вагона от трения в буксах и качения колёс по рельсам Н, где –количество подшипников и – колес вагона; пустого Н.

Записав дифференциальное уравнение движения вагона как точки в центре его тяжести при нулевых начальных условиях, получим следующее уравнение движения груженого вагона:

, (8)

где – масса вагона.

Скорость вагона в конце спуска (точка Е)

. (9)

При движении вагона по прямой АЕ в качестве начальных условий можно принять: и и

. (10)

Если движение вагона осуществляется по ВА, то во всех формулах вместо угла необходимо подставить .

На рис. 2 показаны зависимости от длины прямой скорости в точке для обеспечения скорости м/с и высоты для обеспечения этой скорости при =40 м для груженого и пустого вагона.

Рис. 2 Зависимости от длины горизонтального участка скорости

при необходимой величине скорости =0,6 м/с и высоты ,

обеспечивающей заданную скорость

Анализ полученных зависимостей, проведенных по ним расчетов и существующих рекомендаций позволяет сделать вывод о том, что они позволяют более точно определить скорости вагонов и необходимые длины сортировочных горок.

Литература

1. Николан Е. Л. Теоретическая механика [Текст]: В 2 ч. Ч. 2. / Е. Л. Николан. – М.: Гостехиздат, 1956. – 484 с.

2. Tabor D. The mechanism of rolling friction: the elastic range. – Proc. Roy. Soc., 1955. – P. 198.

3. Бондаренко Л. М. Аналітично-експериментальне визначення коефіцієнта тертя кочення / Л. М. Бондаренко // Будівництво України. – 2001. – №5. – С. 47-48.

4. Писаренко Г. С. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев. – К.: Наук. думка, 1988. – 736 с.

5. Бондаренко Л. М. Уточнення розрахункових схем навантаження групи тіл кочення / Л. М. Бондаренко, С. В. Ракша, М. Г. Брильова // Підйомно-транспортна техніка. – 2005. – № 1. – С. 47-52.