Melkozerov M.G., Alexandrova G.A., Delkov A.V.

Siberian State Aerospace University, Krasnoyarsk, Russia

THEORETICAL AND EXPERIMENTAL RESEARCH OF SWIRLING HETEROGENEOUSNESS DIPHASIC FLOW

Separation of disphasic mediums form the basis of many technological processes. However calculation methods for diphasic mediums used in industry found on empirical studies and can’t lay a claim to universality.

In the offered model of swirling diphasic flow the flow is divided into the viscous interface and the diphasic core. To research the flow of liquid in the area of the viscous interface with big gradients of velocity Navier-Stokes equations are used.

Centrifugal separation of gas-liquid mediums is remarkable for high performance and is widely used in heat exchange and mass transfer equipment. Centrifugal phase separator of various types have become widely spread.

Schematically the construction of centrifugal phase separator (pic. 1) can be presented in the following details:

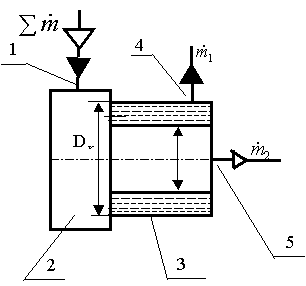
Picture 1. Centrifugal phase separator

- diphasic mixture supply (1);

- device to transform entrance axial flow into the swirled one (the swirler) (2);

- swirling chamber (3);

- circumferential pipe-bend of the gas phase (4);

- central (axial) pipe-bend of the gas phase (5).

Separation of diphasic flow is based on the fact that in the centrifugal field there is separation force that influences gas insertions in the liquid and shifts them to the axis of the chamber. In the centre of the chamber there springs up a gas vortex squeezed by the liquid ring. The separated swirled flow is moving towards the axis, at the outlet of the chamber diverting of separated phases is carried out [1].

In described model the flow in the chamber of the phase separator is conditionally divided into diphasic core and turbulent layer which is δ thick. Friction in the interface is the source of resistance head of the flow.

The interface developed in the swirled flow on the curvilinear surface has a row of peculiarities in comparison with the flat flow. As the result of having longitudinal curve centrifugal forces spring up and hence the pressure gradient does in thickness of the interface. The picture of the flow in this case is similar in many aspects with the flow between rotating cylinders. In this case velocity distribution U on radius R is realized according to the law UR= const (the law of free swirl).

The radial movement of the liquid in the rotating flow is ridden by centrifugal force, resistance force and also by some influence caused by incidental interaction of the particles and the flow.

The free surface of the phases is the surface of equal pressure. This surface is defined by character of pressure distribution in the liquid ring round radius and along the length and also by pressure distribution of in the gas vortex [2,3]. As a rule with minor velocity the pressure distribution is ignored and pressure is considered to be a constant. The border of phases separation gets fixed at the radius when pressure of the gas vortex and the liquid ring are equal.

To design a mathematical model of the swirled flow in the chamber of the phase separator the differential equations system of the movement of viscous incompressible liquid is taken as the original one.

The border of phases gets fixed at the radius when static pressure of the gas vortex and the liquid ring are equal.

The task to integrate equations of the movement of the swirled diphasic flow is considered in the presence of obligatory initial conditions: those of static pressure at the radius R_k; of total pressure at the radius R_k; of static pressure of gas in zero section. The radius of the chamber R_k should be established, mass gas consumption considered to be established and constant.

Generally the task of phases interaction in the swirled flow is characterized by seven equations

The block of equations to characterize the movement of the gas vortex consists of three equations:

· state equation

· energy equation of the gas flow (only axial velocity is taken into consideration)

· continuity equation for the gas flow

These equations define pressure, density and velocity in any section of the gas flow if the accepted constants of the total pressure, its mass consumption and the square of gas flow are known.

The liquid performance is characterized by the following equations:

· energy equation

· continuity equation for the liquid ring

· Bernoulli differential equation (takes account of the axial constituent of the flow velocity in the liquid ring)

The system of these equations is closed and defines parameters of the gas-liquid flow in any section if the dynamic pressure of the liquid in the circumferential direction is known.

In order to turn from the section being considered to the nest section when doing integration, it is necessary to define changes of the dynamic pressure at the step Obviously it will decrease as the swirled flow under the influence of the viscosity will start losing its spin.

Theoretically integration of parameters of the gas vortex can be derived to the endless length, provided its pressure can go down to zero endlessly and the velocity can increase endlessly. In fact the length of the chamber is limited and the hydraulic route behind the chamber of the phase separator doesn’t allow pressure to go lower than the defined value that provides the established gas consumption. Generally in doing calculations for parameters of the flow in the chamber of the definite length with established initial parameters in the zero section the demanded pressure may be attained along the length which is less than the length of the chamber. That means that theoretically the gas vortex squeezed by the liquid ring must get destroyed. If this length approaches to zero, then the phase separating flow can’t exist even in the zero section [4].

Pilot researches are the main test of the theory validity that allows applying the results of theoretical designs for practical purposes. In order to run pilot researches there was produced a pneudraulic test bench with multi-channel method of recording and processing measuring results on the basis of HS A/D transformer that makes it possible to run researches for hydrodynamics of the swirled flow in the chamber of the passive phase separator.

The chamber of the phase separator was presented by a transparent tube with the internal diameter of 44mm and the wall thickness of 13mm. In the reservoir there was a tangential inlet of 8 mm to provide supply and spin of the operating body.

To research the character of the changes of the gas vortex diameter along the length of the chamber the consumption of gas was changed in the range of

3.45×10^-4…1.58×10^-3 kg/s with the constant consumption of the liquid which is equal to = 0.51 kg/s. For each gas consumption one measured total and static liquid pressure in the circumferential area (on the wall) in the initial section of the phase separation and also photographed to measure the diameter of the gas vortex (pic. 2).

Then to define the dependence of length of the gas vortex (or length of the diphasic swirled flow being) on consumption of liquid with the constant gas consumption kg/s one changes liquid consumption in the range of 0,098…0,282 kg/s. With the help of photos the length of the gas vortex was defined (pic. 3).

The analysis of calculation and experimental data showed that accuracy of calculation algorithm is satisfactory and is not higher than 5% in comparison with experimental results.

Picture 2. The swirled diphasic flow with gas consumption . Changes of the gas vortex length 0,042…0,016 m. The gas content in the flow constitutes 0,07 %.

Picture 3. The length of the stable gas vortex l_g.v.= 0.394 m. Liquid consumption . The gas content constitutes 0.16 %.

The designed methods allow to evaluate interdependence of the basic parameters of the swirled monophasic and diphasic flows with tangential supply of liquid and gas-liquid mixture and to define influence of geometry of the chamber flowing part on the basic parameters of the flow.

It is significant that the offered algorithm of calculation for the flow in the chamber of the phase separator takes into account changes of liquid characteristics along the length of the chamber caused by temperature changes of the operating liquid.

The developed model lets not only calculate the nominal regime of the phase separator functioning but also helps foresee possible breakdowns and in advance take measures to eliminate the revealed defects in the process of its designing.

Further research of flow regularities for heat exchange and mass transfer of swirled flows in axial-symmetric channels, systematization of these data and designing universal calculation methods for such flows are topical scientific and practical problem. This research results will be widely applied for purposes of various engineering fields.

References:

1. Brounshtejn B.I., Fishbajn G.A.: Hydrodynamics, mass and heat transfer in disperse systems. Leningrad, Himija, 1977 (in Russian)

2. Chisholm D.: Two-phase flow in pipelines and heat exchangers. Moscow, Nedra, 1986 (in Russian)

3. Uollis G.: One-dimensional two-phase flow. Moscow, Mir, 1972 (in Russian)

4. Melkozerov M.G., Delkov A.V.: ‘Centrifugal phase separator of thermal control systems’. Naukovi praci (Odes'ka nacional'na akademija harchovih tehnologij) 36 (t. 2), Odessa 2009 (in Russian)