Lebedev V.A.

RADIATION CONFIGURATION FACTORS

FOR A FLAT CYLINDRICAL SPIRAL

Institute of Thermophysics SB RAS, Novosibirsk, Russia

Èñïîëüçóÿ ñâîéñòâî îñåñèììåòðè÷íûõ èçëó÷àþùèõ ñèñòåì, èññëåäóåòñÿ àíàëèòè÷åñêàÿ ôîðìà ïðåäñòàâëåíèÿ óãëîâûõ êîýôôèöèåíòîâ ñàìîîáëó÷åíèÿ âíóòðåííåé ïîâåðõíîñòè ëåíòî÷íîé ñïèðàëè è îöåíèâàåòñÿ äîëÿ ëó÷èñòîé ýíåðãèè, «çàïåðòîé» â ïîëîñòè ñïèðàëüíîãî íàãðåâàòåëÿ.

 

Using the properties of axial-symmetric emitting systems, the analytical formula was obtained for a coefficient of self-irradiation of the inner surface of a flat infinite cylindrical spiral.

 

Due to an expanding scope of engineering problems dealing with radiation heat transfer, the necessity of calculation of the radiation configuration factors (RCFs) has emerged in last years. These coefficients Fi - j define the fraction of ray energy emitted from the surface i reaching the surface j. Since 1985 only two handbooks are available ([1] and its following Eds, and [2]) that give information about RCFs for different systems at the level acceptable for engineering applications, although much information has been obtained in this field by numerous researchers for recent years. Before these handbooks were published, data on analytical or numerical form of RCF for a specific configuration of emitting system has been presented only in the monograph [3] (and its oth. Eds), but in amount not sufficient for practical applications. Besides, in these books and the articles from periodic technical magazines, calculations of RCFs (in analytical or graphical forms) for some kinds of emitting systems were not presented yet. For example, among those unexplored objects there are spiral and helical emitting systems. Indeed, the last category is presented in a single paper devoted to Moebius band [4]. 

This paper is an attempt to obtain the RCFs for a spiral emitting system (in particularly, for a flat cylindrical spiral), which has not been presented in publication yet. Here we use the approach proposed in papers [5,6,7] which are recommended for use by authors of [1] and [3].

Fig.1
 
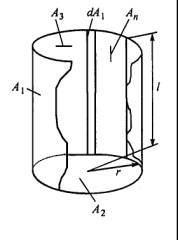Let us consider a RCF Fd   1-2 from an elementary strip dA1 along the whole generatrix of cylinder A1 to the base of cylinder A2 (Fig. 1). We can write an equation which is true for mutual surfaces H1-2 and H2-1 of the emitting system the cylinder’s base – its wall: H2-1 + H2-3 = A2F2-1 + A2F2-3 = A2 (taking into account the closure ratio F2-1 + F2-3 = 1), or, since we have H2-1 + H1-2 = , we obtain

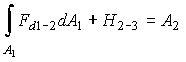.                                               (1)

  Since H2-3 = F2-3A2, then (1) takes the form , after that we have

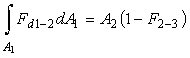.                                           (2)

Substituting into (2) the value , we can write this equation in the form , or , so we can obtain the value of integral RCF from the cylinder wall towards the base of cylinder:

.                                             (3)

The local RCF Fd 1-2 from elementary strip dA1 on the generatrix of the cylinder A1 by its definition depends on area A2 and height dA1. Since A2 is constant and the emitting system has an axial symmetry, we obtain that Fd 1-2 = const (i.e., the magnitude is independent of the position of the strip dA1 on the cylinder wall), then from (2) we have

.                                           (4)

Comparing (3) and (4), we see that F1-2 = Fd 1-2, i.e., RCFs towards the base of the cylinder from the wall and from its elementary strip along its generatrix (of infinite small width) are equal each other. This is a foundation to believe that we have the same RCF from the lateral surface between any two generatrices towards the base of cylinder. This is derived from the properties of reciprocity and closure for RCFs. Let us prove this through an analysis of a discrete case.

Remember that the RCF from one end surface towards another one and towards lateral walls are related through the ratio, which characterizes the property of closure:

F2-1 + F2-3 = 1.                                                 (5)

Splitting the surface A1 into n equal parts An = A1/n (see Fig. 1) between the generatrices and the bases of the cylinder, we present equation (5) in the form:

,

or

,                                               (6)

which is obvious due to axial symmetry of the emitting system. Using the reciprocity relationships , we obtain from (6) RCFs for radiation from An to A2:

,

or

 .                                            (7)

The RCF Fn-2 is independent of the splitting number and transforms into the local RCF for the specific configuration of the system at n ® ¥.

From (3), (4) and (7) we see that F1-2 = Fd 1-2 = Fn-2 = inv, meaning that RCFs are equal by their magnitudes, they are independent of the width of emitting strip, but depend only on radius r of disk A2 and length l of cylinder A1, since only these geometrical parameters affect A1, A2  and F2-3 [1 - 3]:

.

To obtain an RCF for a spiral, we can use the RCF F2-n from the cylinder face A2 to the strip of a final width An, which is parallel to the cylinder axis, on the wall. This RCF can be obtained from (6) or (7) using the reciprocity ratio:

.                                             (8)

Fig.2
 
Let us divide the inner lateral surface of the cylinder into k cylindrical rings of equal height. Then the strip An will be divided by vertical into equal k parts with equal areas Ak (Fig. 2, à). Then the following condition will be satisfied:    , where  are not equal RCFs from the cylinder’s end A2 to equal surfaces Ak, which are equal parts of co-axial rings being at different distances from A2. For that, the magnitudes of F2-n and F2-k  would not change if every ring segment Ak would take an arbitrarily position on its “own” ring. This is derived from the symmetry of the considered system.

Since the position of sections Ak does not affect on the values F2-n and Fn-2 , i.e.,  every section can be arranged arbitrary within its “own” ring, these sections can be arranged as a stepwise spiral (Fig. 2b); for this spiral we can take RCFs Fn-2 at  and . As one can see from (7) and (8), the values of RCF are independent on the horizontal splitting, unlike it was for vertical splitting. Then, at k®¥, Ak ® dAk we obtain the RCFs Fn-2 and F2-n in analytical form of presentation like (3), (4), (7), and (8) for emitting system in the form of a cylindrical spiral, placed between disks A2 and A3, with a radius of r, equal to the spiral radius. The total area of the inner emitting surface of the spiral is 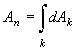. For this splitting, the height of the spiral element dAk becomes infinitely small, and its width, measured in the plane (parallel to planes A2 and A3) remains constant, fixed by the distance between two vertical generatrices ¾ the boundaries of the strip An, whose elements compose the spiral.

Let us consider the self-irradiation of the inner surface of the spiral with radius r with the length l (the height of the forming cylinder A1). If the RCF Fn-1 defines the portion of emission emitted from the strip An (i.e., as it was shown above, from the inner surface of a spiral) to the lateral surface of cylinder A1, then, accounting the closure rule Fn-1 + Fn-2 + Fn-3 = 1 and Fn-2 = Fn-3, and from (7) we obtain:

.                                 (9)

Since for practical calculation the case of a “long” spiral is most interesting, we can consider the situation at l >> r. Then (from the conditions of system’s closure and symmetry) the self-irradiated surface An of a cylindrical flat spiral composes a shear of the lateral inner surface of the cylinder A1; the latter was used for construction of emitting and self-irradiating system in the following proportion: An /A1 = hc /H, where H is the spiral pitch, hc is the width of emitting strip of the spiral (measured in direction parallel to system’s symmetry axis: hc = h /cos a, here h is the width of emitting strip, a is the inclination angle of the spiral turn (see Fig. 2, b). Then from this reasoning and from (9) we obtain that Fn-n / Fn-1 = An / A1 = hc /H and RCF for self-irradiation of a spiral is as follows:

.                              (10)

For a case of a “long spiral” we have r/l ® 0. Then one can see from the geometry of the system that (A2/A1) ® 0 and F2-3 ® 0; so RCF for self-irradiation of a flat cylindrical spiral (the band was transformed into the spiral) takes the following analytical form:

,                                        (11)

which is extremely simple and useful for practical calculations.

References:

1. J.R. Howell,  A Catalog of Radiation Configuration Factors. McGrow-Hill Book Co., N. Y., San Francisco, Toronto, 1983, 1985 & www.engr.ukyedu/rtl/Catalog/

2. N.A. Rubtsov, V.A. Lebedev, Geometric Invariants of Emission, Novosibirsk, 1989.

3. R. Siegal, J.R. Howell, Thermal Radiation Heat Transfer. (4th edition,Teylors & Francis), N. Y., 2001.

4. A.L. Stasenko, The self-radiation of Moebius band with a fixed shape, Izvestiya AN SSSR, ser. Energetika i Transport, n. 4, pp.104 - 107,1967.

5. V.A. Lebedev, Invariance of radiation shape factor for certain radiating systems, Izvestiya SO AN SSSR, ser. Techn. Nauk, n. 13, iss. 3, pp. 73 - 77, 1979.

6. V.A. Lebedev, About relationships between radiation configuration factors for cylindrical emitting systems, Soviet Journal of Applied Physics, Vol. 11, n. 3, pp. 12 - 16, 1988.

7. V.A. Lebedev, Geometricheskie invarianty izlucheniya spiralevidnyh nagrevateley, Teplofizika i Aeromekhanika, Vol. 10, n. 1, pp. 101 - 108, 2003.