Технические науки/ 5. Энергетика

К.т.н. Ершов Ю.А., инженер Киселев Д.Н.

Сибирский федеральный университет, Россия

РАЗРАБОТКА ПРОГРАММНЫХ МОДЕЛЕЙ ДЛЯ ИССЛЕДОВАНИЯ МИКРОПРОЦЕССОРНЫХ ДИСТАНЦИОННЫХ ЗАЩИТ

В результате развития компьютерных технологий появилась возможность виртуального испытания устройств релейной защиты. Современные программы визуального объектно-ориентированного моделирования позволяют создавать очень сложные и детальные динамические модели устройств релейной защиты. Эти модели дают возможность отслеживать входные и выходные данные, а также промежуточные расчёты. Таким образом, можно анализировать работу устройств релейной защиты в режиме реального времени и проверить правильность их функционирования при различных режимах электрической сети.

В данной статье представлена программная модель дистанционной защиты. При её реализации была задействована программа Matlab.

Разработанная модель имитирует функции современных дистанционных защит от междуфазных коротких замыканий. Модель позволяет изучить особенности работы измерительных органов и логики устройств дистанционной защиты. С её помощью можно производить расчёты защит, визуально контролировать прохождение сигнала по логическим схемам, а также прослеживать состояния сигнальных органов при ручном задании уставок и режима электрической сети. Кроме того, в модели возможно осциллографирование сигналов в любой цепи и на выходе блоков логических схем.

Таким образом, данная модель может использоваться для виртуального испытания существующих устройств релейной защиты. С помощью модели можно своевременно выявить ошибки, возникшие из-за неучёта каких-либо факторов. Кроме того модель отлично подходит для обучения персонала, для лабораторных и научных целей.

Целью представленной статьи является разработка виртуальной модели дистанционной защиты, интегрированной со схемами энергетических систем. Это позволяет детально проанализировать процессы, протекающие как в первичной силовой цепи, так и в цепях релейной защиты, что имеет огромное значение для научного и для образовательного процесса.

Виртуальная модель дистанционной защиты выполнена стандартными блоками Simulink и подсистемами, отражающими логику и алгоритм работы.

Функциональная схема разработанной защиты показана на рис. 1.

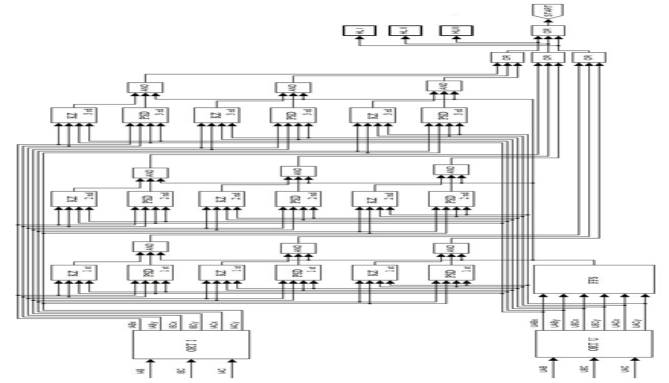
Рис. 1 – Функциональная схема дистанционной защиты

В состав модели дистанционной защиты входят формирователи ортогональных составляющих тока и напряжения (модули ORT I и ORT U). Эти модули осуществляют преобразование входных сигналов для получения величин, используемых в алгоритмах измерительных органов защиты. Таким образом, они являются промежуточным звеном между измерительными трансформаторами и измерительными органами защиты. Формирователи ортогональных составляющих тока и напряжения имеют один принцип действия.

Рассмотрим формирователь ортогональных составляющих тока ORT I.

На вход данного модуля поступают дискретные сигналы, представляющие собой величины, пропорциональные токам защищаемой линии электропередачи. Закон изменения этих величин можно представить в следующем виде:

где I – ток, поступающий на вход модуля,

Im – амплитудное значение тока I.

Измерительные органы сопротивления данной модели ДЗ оперируют с комплексными величинами. Поэтому для работы измерительных органов защиты необходимо комплексное значение тока:

где - закон изменения тока по фазе;

– закон изменения тока по величине.

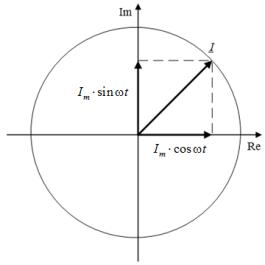
Рис. 2 – Ортогональные составляющие тока

Токи и представляют собой ортогональные составляющие, (рис. 2).

Таким образом, моделирование формирователей ортогональных составляющих производится путём представления мгновенных значений токов и напряжений в виде ортогональных составляющих. Все вычисления осуществляются в режиме реального времени. Причём в приложении Simulink предусмотрена возможность изменения частоты дискретизации сигнала, что позволяет изменить точность расчёта.

Принцип действия цифрового органа сопротивления KZ основан на расчёте полного сопротивления линии путём деления мгновенных значений ортогональных составляющих напряжения Ux, Uy и тока Ix, Iy, поступающих в режиме реального времени от формирователей ортогональных составляющих ORT I, ORT U.

При этом характеристика срабатывания органа сопротивления задаётся аналитически уравнениями линий. Поэтому его алгоритм работы состоит из двух частей: вычисления сопротивления и проверки предварительно заданных условий срабатывания органа.

Функциональная схема цифрового органа сопротивления представлена на рис. 3.

Рис. 3 – Функциональная схема органа сопротивления

Действительная (активная) и мнимая (реактивная) части сопротивления определяются по формуле

Во второй части алгоритма производится проверка выполнения условий срабатывания органа: годограф полного сопротивления Z должен находиться в предварительно заданной зоне срабатывания.

Для ограничения области действия органа сопротивления задается характеристика срабатывания. На рис. 4 представлены характеристики срабатывания для трёх ступеней дистанционной защиты.

Рис. 4 – Характеристики срабатывания органов сопротивления

Характеристика срабатывания задается путём ввода уставок по сопротивлениям R01, R02, X01, X02 и по углам b1, b2, b3, b4 в диалоговое окно ввода параметров, рис. 5.

Рис. 5 – Диалоговое окно ввода параметров

Таким образом, характеристика срабатывания для органов сопротивления каждой ступени получается аналитически, с помощью уравнений четырех прямых:

Проверка выполнения условий срабатывания органа сопротивления производится по следующему алгоритму (рис. 6).

Рис. 6 – Алгоритм проверки выполнения условий срабатывания

Таким образом, если годограф полного сопротивления Z находится в зоне действия, то есть не выходит за пределы характеристики срабатывания, то на выходе модуля KZ появляется логическая единица. Это сигнализирует о срабатывании органа сопротивления.

В разработанной модели блокировки при качаниях (PSD) сначала производится вычисление сопротивлений по алгоритму, который изложен выше. Дальнейшая работа данного органа основывается на определении времени, которое необходимо для прохождения годографа полного сопротивления Z между внешней и внутренней границами характеристики срабатывания. Если это время превышает то, что задано уставкой, то модель выявляет качания в энергосистеме.

Рассмотрим программную реализацию модели.

Для ограничения области действия блокировки при качаниях задается характеристика срабатывания (рис. 7)

Рис. 7 – Характеристика срабатывания блокировки при качаниях.

Характеристика срабатывания блокировки задаётся уставками по сопротивлениям и по углам: . Эти уставки формируют восемь уравнений прямых, определяющих внутреннюю и внешнюю границы характеристики срабатывания:

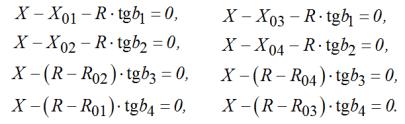
Проверка выполнения условий нахождения годографа полного сопротивления Z в зоне действия блокировки при качаниях производится по алгоритму, представленному на рис. 8.

Если время нахождения годографа полного сопротивления Z превышает, заданное уставкой в блоке KT1 (выдержка времени), то на выходе модуля PSD появляется логический ноль. Это свидетельствует о качаниях в энергосистеме и модуль PSD блокирует действие ДЗ. При КЗ, время нахождения годографа полного сопротивления Z не превышает, заданное уставкой. На выходе модуля PSD появляется логическая единица, то есть происходит ввод в действие ДЗ на время, заданное уставкой t.

Моделирование блокировки неисправности цепей переменного напряжения (FFS) основано на выявлении изменения напряжения. В случае короткого замыкания, напряжение близко к нулю, но не всегда равно ему. Орган неисправности цепей переменного напряжения в режиме реального времени выявляет изменения напряжения, и в случае его отсутствия блокирует работу дистанционной защиты.

Рис. 8 – Алгоритм задания зоны действия блокировки

Рис . 9 – Схема лабораторного стенда

Разработанная модель дистанционной защиты – трёхступенчатая. Условия срабатывания каждой ступени – наличие логических единиц на выходах KZ, PSD, FFS. При запуске ступени защиты, срабатывает соответствующий сигнальный орган HL и исполнительный орган Start (рис. 1).

Для моделирования электрических режимов и виртуального испытания устройств дистанционной защиты была создана специальная модель трехфазной электрической сети (рис 9).

Модель предусматривает задание всех необходимых параметров: системы (GS1, GS2), выключателей (Q1, Q2), линий (W1, W2), нагрузок (H1). Кроме того можно задать все режимы работы сети и получить необходимые токи КЗ с помощью короткозамыкателей (QN1, QN2, QN3, QN4). Эта модель связана с моделью дистанционной защиты (Distance protection) через модели измерительных трансформаторов тока (ТА1) и напряжения (TV1), что позволяет получить интегрированную модель для виртуального испытания устройств дистанционных защит.

Испытание модели дистанционной защиты производится в следующем порядке:

1. Расчёт параметров первичной цепи.

2. Запуск настроенной модели электрической сети.

3. Получение ортогональных составляющих необходимых токов и напряжений

4. Расчёт уставок дистанционной защиты задающих форму зоны срабатывания

5. Выставление уставок и повторный запуск модели

6. Получение результатов испытаний в виде осциллограмм и анализ работы органов защиты путём контроля входных и выходных данных на каждом из них.

Разработанная модель позволяет исследовать как основные органы защит, так и полностью дистанционные защиты, как в лабораторных, так и научных целях.

Литература:

1. Ершов Ю. А., Бойко А. С., Михайленко Я. В. Цифровые цепи тока и напряжения. Применение в релейной защите. Журнал “Новости ЭлектроТехники” г. Москва №6 2006г стр. 11-14.

2. Овчаренко Н. И. Аппаратные и программные элементы автоматических устройств энергосистем. – М.: Изд-во НЦ ЭНАС, 2004. - 512 с.: ил.

3. Киселев Д.Н., Ершов Ю.А. Моделирование органа сопротивления в операционной среде Matlab.// Томск.: Энергетика : экология, надежность, безопасность : Труды XII Всероссийского студенческого научно-технического семинара : в 2-х томах: сборник научных трудов//– Томск ТПУ, 2010 – 86-89с.