Технические науки/ 5. Энергетика

 

Анкудинова М.С., к.т.н. Сандалова Л.А., к.т.н. Ларин Е.А.

 

Саратовский государственный технический университет
 имени Гагарина Ю.А., Россия

 

МАТЕМАТИЧЕСКАЯ  МОДЕЛЬ РАСЧЕТА
 БЕЗОТКАЗНОСТИ ПАРОГЕНЕРАТОРОВ
 ПАРОГАЗОВЫХ УСТАНОВОК


      Управление надежностью при проектировании энергетического оборудования с целью оптимизации конструктивных, технологических, схемных и эксплуатационных решений требует разработки моделей и методов расчета единичных показателей надежности (ПН) элементов энергооборудования. Модели надежности элементов энергооборудования и энергоустановок в целом создаются на основе анализа их функционального назначения  с учетом действительных факторов и условий работы, достоверности исходной информации, требуемой точности результата оценки надежности. Детерминированные методы расчета ПН элементов энергооборудования, получившие достаточно широкое применение и основанные на расчете относительных или абсолютных запасов прочности и долговечности, не учитывают ряда реальных эксплуатационных факторов. В действительных условиях эксплуатации значения служебных характеристик  металла (предел длительной прочности, предел усталости и др.) и действующих напряжений носят случайный характер из-за случайных нарушений  стационарных  режимов  работы  и отклонений  характерных размеров элементов вследствие производственных, технологических и эксплуатационных факторов. Поэтому расчет ПН элементов энергооборудования должен базироваться на основе вероятностных методов, позволяющих учесть статистическое рассеяние характеристик прочности и нагруженности с использованием теории случайных величин и случайных функций.

Надёжность парогенераторов (ПГ) парогазовых установок (ПГУ) определяется:

-термонапряжённым состоянием  трубного пучка, температурный режим которого зависит от параметров теплоносителя, конструктивных особенностей, конструкционных материалов, режимов эксплуатации и ряда других факторов;

-в отдельных зонах ПГ возникают пульсации температур, вызванные особенностями  генерации пара и нестационарностью расходов, давлений и температур теплоносителей. Одним из самых опасных с точки зрения разрушения  является участок ухудшенного теплообмена испарительной зоны ПГ. Причиной пульсаций температуры стенки труб ПГ является изменение локальных коэффициентов теплоотдачи из-за высыхания микроплёнки жидкости на внутренней образующей труб испарительной части. Пульсации температур вызывают соответствующие пульсации термических напряжений, которые, суммируясь  со стационарными напряжениями, снижают надёжность ПГ. Так как пульсации температур и напряжений носят случайный характер, а служебные характеристики материалов имеют статистическую природу, то расчёт показателей надёжности должен базироваться на использовании вероятностных подходов.

В основу математической модели расчета одного из важнейших единичных показателей надёжности ПГ, его безотказности, положено следующее:

- ПГ делится на зоны, каждая из которых вносит свой вклад в вероятность отказа. При этом экономайзерная зона содержит четыре участка, испарительная имеет участки развитого кипения и ухудшенного теплообмена, перегревательная зона состоит из двух участков;

 - действующие напряжения являются случайными величинами, разброс которых относительно математического ожидания определяется глобальными и локальными факторами. Глобальные неопределённости характерны для всех зон ПГ, определяются местными условиями и связаны с уменьшением толщин стенки из-за технологических факторов, эрозии, коррозии и т.д. Все локальные неопределённости статистически независимы, поэтому для получения общего закона распределения случайной величины напряжений могут быть использованы свёртки отдельных функций;

- служебные характеристики применяемых материалов (предел длительной прочности и предел выносливости) являются случайными величинами, распределёнными по нормальному или логарифмически нормальному законам;

- оценка безотказности проводится из условия определения вероятности непревышения действующих напряжений над допустимыми на каждом расчётном участке. Для определения этого условия используются свёртки дифференциальных функций распределения действующих напряжений и их предельных значений.

В соответствии с феноменологичеким подходом к расчету надежности элементов энергооборудования [1] под безотказностью элемента следует понимать вероятность непревышения величины нагружения  прочности , то есть попадания случайной функции работоспособности (ФР) Z(t)= Y(t) - X(t) в область отрицательных значений. Значения аргументов функции X(t) и Y(t) в общем случае определяются их номинальными значениями  и  ,  а также постоянными  и  и  переменными во времени   и  отклонениями. Если в ПГ выделено  элементов, а безотказность каждого из них характеризуется  ФР, то условие безотказности запишется в виде

,

где k-количество анализируемых зон ПГ.

          Таким образом, функция работоспособности  является случайной функцией, колеблющейся около некоторого случайного стационарного уровня , положение которого определяется постоянными во времени отклонениями аргументов  и  от  математического ожидания , рассчитываемого по номинальным значениям и .

Случайные колебания ФР около определяются стационарными случайными функциями изменения расхода  , давления  , температуры  и описываются законом

,

где , ,   - среднеквадратичные отклонения  ФР из-за переменных во времени локальных и глобальных отклонений.

В общем случае, когда несколько ФР определяют безотказность, то есть при , вероятность безотказной работы запишется в виде

                      .                                                                   (1)

Если ФР   зависимы, то формула (1) принимает вид

.

Если ФР  независимы, то

.

Математическое ожидание действующих эквивалентных напряжений трубного пучка парогенератора, в том числе  для оребренных труб, определяется перепадом давлений теплоносителей и температур на стенке и рассчитывается по методике, изложенной в [2].

Вероятность того, что для m - го участка ПГ (опуская индекс m) действующие напряжения превысят допустимые, то есть  , определится как

                        ,                                                    (2)

где - совместная дифференциальная функция распределения вероятностей приведённых напряжений и длительной прочности.

Так как условие работоспособности участка ПГ имеет вид, то используя его для определения областей интегрирования (2), получим

.

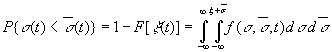Наряду со стационарными напряжениями трубный пучок испарительной зоны ПГ испытывает переменные термические напряжения, обусловленные пульсациями температур. Наибольший размах температурных пульсаций достигается на участке ухудшенного теплообмена и обусловлен поочередным омыванием внутренней стенки трубки ПГ кипящей водой и паром. Максимальное значение температурных пульсаций  не превышает значения , где  - температура греющей среды (продуктов сгорания после газовой турбины) в соответствующей зоне ПГ, оC;  - температура насыщения, оC . Размах температурных пульсаций определяется условиями теплопередачи и рассчитывается по формуле

,

где  ,   - коэффициенты теплоотдачи при ухудшенном теплообмене и режиме развитого кипения, Вт/(м2.гр); ,  -  термические сопротивления теплоотдачи от газа к стенке и сопротивление стенки, (м2.гр)/Вт.

Так как величина , то амплитуда температурных напряжений , значения которых определяются как

.

Учитывая, что , можно считать, что случайная величина  распределена по усечённому закону Рэлея с параметрами   и  , то есть

,

где - параметр усечения, определяемый из условия нормировки .

Расчёт на усталость проводится из условия сравнения эквивалентных амплитуд , приведённых к симметричному циклу, с пределом выносливости или путём сравнения рабочих амплитуд напряжений с предельными значениями. Воспользуемся вторым подходом. При этом предельная амплитуда напряжений . Приняв величины  и   случайными и распределёнными по нормальным законам, параметры распределения предельной амплитуды напряжений определяется как

,

где , ,  ,  - соответственно математические ожидания и дисперсии соответствующих случайных величин.

Расчёт вероятности  безотказной работы при усталостном нагружении участка поверхности теплообмена ПГ сводится к определению вероятности непревышения амплитуды рабочих напряжений   допустимых значений . Для получения этой вероятности  проинтегрируем плотность вероятности совместной функции распределения случайных величин   и , умноженную на дифференциалы аргументов по областям их изменения, определяемым неравенствами    и                                         

                                    .                                

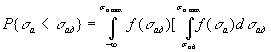Учитывая вклад каждого змеевика в общую надёжность, вероятность безотказной работы ПГ определится как

,

где m - количество змеевиков в парогенераторе.

Разработанная вероятностная модель расчёта безотказности ПГ позволяет выявить влияние термодинамических параметров рабочего тела энергоустановки и конструктивных характеристик ПГ на показатели надёжности ПГ.

Список используемой литературы

1. Надежность теплоэнергетического оборудования ТЭС и АЭС. /Под ред. А.И. Андрющенко. М.: Высшая школа,  1991. – 240 с.

2. Расчет и рекомендации по проектированию поперечно-оребренных конвективных поверхностей нагрева стационарных котлов. РТМ 108.030.140-87. М.:1988. – С.30