УДК 621.317.08; 621.317.1; 621.317.6
ЛИНГВИСТИЧЕСКАЯ МОДЕЛЬ ИЗМЕРЕНИЙ
Ю.Н. Кликушин
Омский государственный технический университет (ОмГТУ)
Аннотация. Предлагается лингвистическая модель, которая
учитывает влияние на результат измерения всех реперных точек шкалы. Алгоритм модели формирует три списка, два из
которых представляют собой прямо и обратно упорядоченные последовательности
имен реперных точек, задающие пределы измерения. Третий список, формируемый под
воздействием входной величины, является неупорядоченной последовательностью
имен реперных точек. Если измерить степень неупорядоченности (хаотичности)
третьего списка, то можно получить численные оценки измеряемой величины и ее
неопределенности.
Ключевые слова: измерение, интерполяция,
классификационные свойства, лингвистическая модель, неупорядоченность,
неопределенность результата, хаос положения, шкала.
Abstract. A linguistic model which takes into account influence on the result of
measuring of all refer points of scale is offered. A model algorithm is formed by three lists, two from which are
straight and back well-organized sequences of the names of refer points,
questioner measuring limits. The third list, formed under act of entrance size,
is the unregulated sequence of the names of refer points. If to measure the
degree of inefficiency (to chaotic ness) of the third list, it is possible to
get numeral estimations of measured and its vagueness.
Keywords: measuring, interpolation, chaos of position, classification
properties, linguistic model, inefficiency, scale, vagueness of result.
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим
ситуацию (рисунок 1), при которой измерению подлежит постоянный ток Jx,
лежащий в диапазоне от 0 до 10 А. Шкала показывающего прибора имеет 6
оцифрованных отметок в том же диапазоне. Под воздействием входной величины
стрелка прибора отклонилась от нулевой отметки на некоторый угол. Поскольку
между оцифрованными отметками делений нет, то задача измерения сводится к
задаче интерполяции положения стрелки между двумя соседними отметками 2 и 4 А.

Рисунок 1 – Пример, иллюстрирующий
постановку задачи
При
этом возможны два алгоритма интерполяции. Первый из них предполагает переход к
номинальной шкале, у которой есть только два значения (слева и справа от
указателя). Поэтому суждение о неизвестном значении измеряемой величины должно
быть таким: «Значение тока равно либо 2, либо 4 А». Второй вариант предполагает
использование некоторых дополнительных, априорных сведений о характере
распределения значений между отметками. Так, например, если используется
измерительный механизм магнитоэлектрической системы, то предполагается, что существует линейная функция
принадлежности положения стрелки к отметкам шкалы. В этом случае можно
применить понятие расстояния и значение входной величины определять, например,
по принципу принадлежности стрелки к той отметке, расстояние до которой
минимально.
На
практике, в рассмотренной ситуации для увеличения точности интерполяции
применяются два способа: увеличение количества реперных точек в том же
диапазоне и переключение пределов измерения.
Однако,
в любом случае положение стрелки всегда будет определяться с
использованием только двух отметок (из N
возможных). Следовательно, эффективность использования измерительной шкалы в самом простом варианте (рисунок 1) составляет
всего одну треть (1/3).
Таким
образом, сформулируем проблему, как задачу разработки такого алгоритма интерполяции, при котором учитывалось
бы влияние всех реперных точек шкалы в оценку положения стрелки указателя.
АЛГОРИТМЫ
ЛИНГВИСТИЧЕСКОЙ ИНТЕРПОЛЯЦИИ
Главная идея
алгоритмов лингвистической интерполяции (рисунок 2) базируется на целостном
представлении шкалы, основным агрегированным свойством которой является ее
упорядоченность [1,2]. Работа алгоритмов
связана с обработкой списков имен реперных точек. Можно указать 3 основных
алгоритма: А) формирования измерительной шкалы; Б) получения результата
измерения и В) оценки функции неопределенности результата измерения.
Алгоритм
формирования измерительной шкалы. В блоке 1 осуществляется ввод измеряемого значения Jx тока. В блоке 2
производится вычисление модуля разности значения Jx и массива реперных
точек: Di = abs(Jx –
Zi), где Zi – значение i-ой
реперной точки. Блок 3 является базой данных, в которой хранится виртуальная
шкала. В блоке 4 осуществляется контроль полноты просмотра всех (N = 6) реперных точек. На
выходе этого блока формируется массив {D},
который представляет собой список отклонений
Di по всем реперным точкам
{D} = {D1, D2,.,Di,..,DN}.
Этот массив сортируется {Ds} по возрастанию в блоке
5. Перебор реперных точек эталонов производится в счетчике 6. Вывод полученного
списка эталонов осуществляется в блоке 7.
Алгоритм
получения результата измерения. Вступает в действие после того, как будут
сформированы основные компоненты лингвистической модели измерения (рисунок 3). В
рассматриваемом примере реперные точки шкалы обозначены символами латинского
алфавита (0 → A, 2 → B, 4→ C, 6→
D, 8→ E, 10→ F),
из которых можно образовать две абсолютно упорядоченные шкалы.
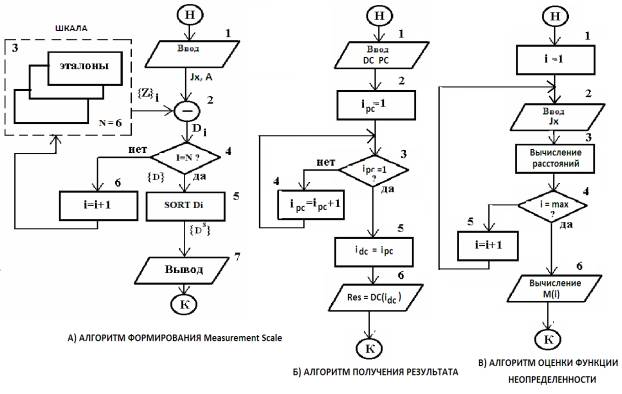
Рисунок 2 – Структурные схемы алгоритмов
лингвистической интерполяции

Рисунок 3 – Компоненты лингвистической
модели измерений
Первая шкала
представляет собой прямую последовательность символов ABCDEF и называется прямой
шкалой (Direct Scale), а вторая – обратную
последовательность FEDCBA и называется обратной
шкалой (Reverse Scale).
Прямая
(Direct Scale) и обратная (Reverse
Scale) шкалы задают левую (J = 0, А) и правую (J =
10, А) границы диапазона измерений, расстояние между которыми постоянно.
Измерительная шкала (Measurement Scale)
представляет собой неупорядоченную (перемешанную) последовательность тех же
символов алфавита, полученную при измерении входной величины Jx.
Если
значение (Jx) входной величины меняется, то меняется положение Measurement Scale и степень ее неупорядоченности, причем
наибольшая хаотичность будет соответствовать центральному положению
измерительной шкалы. Следовательно, понятие «хаос» можно использовать для
количественной оценки положения
измерительной шкалы относительно крайних отметок (Direct
Scale и Reverse Scale).
Будем называть такой хаос статическим (хаосом положений), в отличие от динамического хаоса, который
является результатом наличия движения элементов системы [3,4].
Измерительная
шкала (Measurement Scale) состоит из 3-х
связанных списков: Distance (DC),
Position Code (PC),
Lingvo Code (LC).
Список типа Distance является перечислением
упорядоченных отклонений {Ds}. Список типа Position Code
перечисляет порядковые номера (ранги) реперных точек, выстроенных в
соответствие со списком Distance. Список типа Lingvo Code
представляет собой кодированный символами алфавита список PC.
Возможности
лингвистической модели (рисунок 3) определяются следующими обстоятельствами.
Во-первых, модель позволяет сформировать уравнение измерения, указав численное
значение входной величины и способ его получения. Записанное на рисунке 3
уравнение измерения следует читать так: «Численная
оценка измеряемой величины находится в той ячейке списка отклонений типа Distance (DC) измерительной шкалы,
на которую указывает единица («1» = ранг начальной отметки прямой шкалы) из
списка Position Code (PC) измерительной шкалы». Следуя этому правилу, находим, что Jx
=2,5 А. Другими словами, имея те же 6 реперных точек (рисунок 1), мы получили
точное значение измеряемой величины без привлечения дополнительных априорных
данных о характере шкалы.
Во-вторых,
наряду с результатом измерения, алгоритм выдает оценку степени его
неопределенности. Эта оценка основана на измерении относительного расстояния
между измерительной и граничными шкалами.
ЛОГИЧЕСКАЯ СХЕМА ВЫЧИСЛЕНИЯ
НЕОПРЕДЕЛЕННОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
На
рисунке 4 представлены модель (А) вычисления расстояния между шкалами. В нижней части рисунка изображена функция
принадлежности (Б) результатов измерений к прямой и обратной шкалам, а также ее
аналитическое выражение. Алгоритм оценки функции принадлежности (неопределенности) изображен на рисунке 3,
В).
В
частности, расстояние между шкалами определяется как сумма, взятых по модулю,
разностей значений рангов одинаковых позиций сравниваемых шкал:
![]() ,
, ![]()
![]() (1)
(1)
Чтобы
построить всю характеристику неопределенности, надо просканировать значение
входной величины в заданном диапазоне (от 0 до 10 А) и измерить относительные
расстояния (М = Position Coeff).
Полученная таким образом эмпирическая характеристика (рисунок 4, Б), будет
иметь ступенчатый характер, в силу ограниченного числа (N =
6) реперных отметок шкалы. Для линейных шкал количество ступеней квантования
можно подсчитать по формуле:
![]() . (2)
. (2)
.
В частности, для N =
6, q = 10 и цена деления новой, виртуальной шкалы составит: С = (10
А)/2*q = 0,5 A (против 0,83 А – для
исходной модели, рисунок 1). Следовательно,
с помощью предлагаемого алгоритма удалось повысить эффективность измерения в
1,67 раз.
Непрерывная
модель характеристики неопределенности (рисунок 4) получена с помощью программы
TCWin (фирмы Jandel Scientific)
из более, чем 4000, хранящихся в базе данных этой программы.
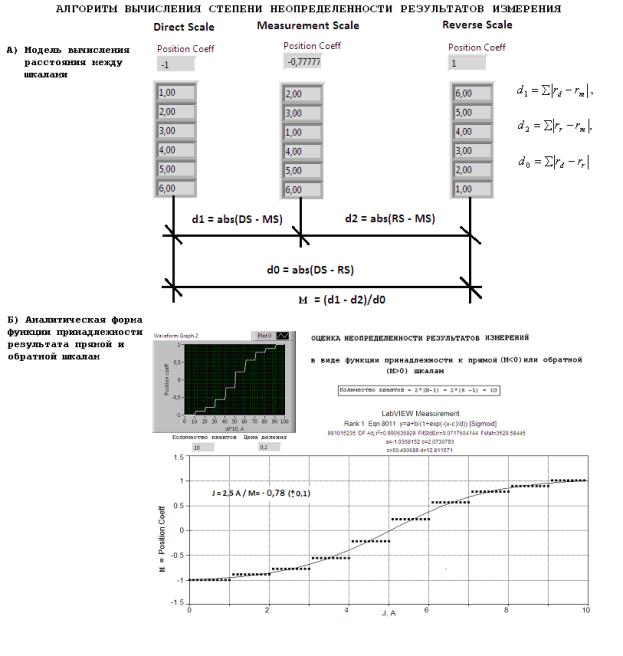
Рисунок 4 – Логическая схема вычисления степени
неопределенности результатов измерения
При
этом, наилучшей моделью (Eqn 8011, Rank
= 1) характеристики неопределенности оказалась сигмодальная (Sigmoud)
функция:
![]() , (3)
, (3)
где:
A =-1; B =2; C =
5; D = 12,8 – параметры модели; X = Jx
– входная
независимая переменная (ток); Y = M = Position Coeff. Физический смысл параметров модели
заключается в том, что коэффициент “A” – определяет
минимальное значение (-1) характеристики неопределенности, “A+B” =
1 - определяет максимальное значение характеристики неопределенности,
коэффициент “C” – задает положение нуля, а коэффициент “D” – задает крутизну
характеристики неопределенности.
С
позиций теории нечетких множеств [5], характеристика (3) является функцией
принадлежности результата измерения (Jx) к прямой и обратной
шкалам. При этом, знак минус означает, что результат измерения находится ближе
к прямой шкале, а знак плюс – к обратной. В рассматриваемом примере результат
измерения (Jx =2,5 А) принадлежит левой границе (прямой шкале) примерно
на 78%.
Физический
смысл характеристики неопределенности (3) состоит в том, что, она измеряет степень
неупорядоченности измерительной шкалы, которая в данном случае составляет 22%.
Подобную неупорядоченность можно классифицировать, как детерминированный хаос положений.
С
математической точки зрения, характеристика
(3) является интегралом от распределения степени неупорядоченности
(хаоса). Поэтому можно провести аналогию между вероятностными характеристиками
(функцией и плотностью распределения вероятностей) и «шкальными»
характеристиками (функцией принадлежности и распределением хаотичности) лингвистической
модели.
С
помощью формулы (2) лингвистической модели можно оценивать неопределенность
характеристики (3). Для этого
необходимо диапазон (от -1 до 1) изменения (∆M =2) этой характеристики
по оси ординат разделить на удвоенное количество (k = 2q) ступеней
квантования. В рассматриваемом примере получается оценка, равная ±0,1.
Следовательно, окончательно результат измерения с помощью лингвистической
модели может быть записан в виде:
![]() , (4)
, (4)
где: idc,
jpc
– порядковые номера ячеек списков типа Distance и
Position Code,
соответственно, ∆J
= Jx
– значение измеряемой величины, хранящееся в ячейке idc списка Distance, M(∆J) – степень
принадлежности результата ∆J
измерения прямой (М<0) или обратной (M>0) шкалам.
ВЫВОДЫ
Предлагаемая модель названа лингвистической потому,
что принцип ее работы связан с обработкой списков, в качестве которых выступают
последовательности имен реперных точек (шкалы).
1.
Лингвистическая модель устанавливает такой алгоритм
(4) получения результата измерения, который не зависит от нелинейности
использованной шкалы. Нелинейность виртуальной шкалы влияет лишь на параметры (С
и D)
характеристики неопределенности (3). Вид этой функции (сигмодальная) и
параметры (А и В) остаются постоянными.
2.
Виртуальная шкала может быть легко адаптирована к
диапазону возможных изменений входной величины, заданием нижнего и верхнего
пределов. Например, если априорно, известно, что входной ток может изменяться
от 3 до 8 мкА, соответственно, надо выбирать нижний предел 3 мкА, а верхний – 8 мкА.
3.
Количество реперных точек выбранного диапазона
следует выбирать, исходя из требуемой дискретности шкалы неопределенности. Например,
задавая шаг дискретизации 0,5 мкА, в диапазоне от 3 до 8 мкА можно создать 11
реперных точек. Соответственно, по формуле (2)
получим 20 ступеней
квантования и размытость функции принадлежности (3) порядка ±0,05.
4.
Лингвистическая модель обладает классификационными
возможностями. В частности, на рисунке 3 показана общая часть (Root, корень),
связывающая прямую и измерительную шкалы и образующая ствол классификационного
дерева. С помощью подобных классификационных структур можно визуализировать
латентные (скрытые) закономерности в
структуре числовых данных любой физической природы.
Перспективы
применения лингвистической модели связаны с построением интеллектуальных цифровых
измерительных приборов со встроенными виртуальными шкалами. В познавательном
смысле лингвистическая модель может стать новой парадигмой измерений,
основанной на количественной оценке хаоса положений (статический хаос) и его
изменений во времени (динамический хаос).
Материалы исследования получены в рамках выполнения
государственного контракта № 16.516.11.6091 по теме: «Проведение поисковых
научно-исследовательских работ в области разработки и создания оборудования для
диагностики и эксплуатации энергетического оборудования».
Литература
1.
Горшенков
А.А., Захаренко В.А., Кликушин Ю.Н. Температурная шкала для
распределений вероятности.// Интернет издание «Журнал Радиоэлектроники». - М.:
Изд-во ИРЭ РАН, № 10(октябрь), 2010. http://jre.cplire.ru
2. A.A. Gorshenkov, V.A. Zakharenko, Yu.N. Klikushin, S.A. Orlov A SYSTEM
APPROACH TO THE DESCRIPTION OF THE PROPERTIES OF THE ITS-90//Measurement
Techniques, Vol.54, No 8, November, 2011, pp. 901-909. – Springer Science +
Business Media Inc.
3. Анищенко В. С.
Сложные колебания в простых системах. Механизмы возникновения, структура и
свойства хаоса в радиофизических системах. - М.: Наука, 1990.
4.
Дмитриев А. С. Хаос и обработка информации в нелинейных
динамических системах //Радиотехника и электроника. 1993. Т. 38. № 1. С. 1 – 24.
5. Нечеткие множества в
моделях управления и искусственного интеллекта // Под ред. Д.А.Поспелова. – М.:
Наука, 1986.
СВЕДЕНИЯ ОБ АВТОРЕ
1.
Кликушин
Юрий Николаевич, д.т.н., профессор кафедры «Технология электронной аппаратуры» (ТЭА)
Омского государственного технического университета (ОмГТУ)
2.
Тел.
(раб) (3812) 65-26-69, сот. 8-913-613-16-36
3.
E-mail: iit@omgtu.ru
4.
Адрес
(дом): 644050, Омск, ул. 20 партсъезда, д. 15, кв. 5.
5.
Адрес
(раб): 644050, Омск, пр. Мира, д. 11, ОмГТУ.