к.т.н. Дьяков И.А., д.т.н. Литовка Ю.В., д.т.н. Ткачёв А.Г.,
д.т.н. Туголуков Е.Н, аспирант Мухин Р.Ю., аспирант Гравин
А.А.
Тамбовский
государственный технический университет, Россия
Математическое моделирование
теплоотдачи
наномодифицированных электрохимических
покрытий
Повышение теплоотдачи от элементов
энергетического оборудования является актуальной задачей. Одним из способов её
решения является изменение свойств теплоотдающей поверхности, в частности,
увеличением шероховатости. Для достижения этой цели авторами предложен способ,
заключающийся в нанесении наномодифицированного гальванического покрытия на
теплоотдающие поверхности. При этом на поверхности образуются выступы высотой
30 – 40 мкм и преодолевается приповерхностная часть теплового пограничного
слоя, соответствующая высоте выступов рельефа поверхности.
Для оценки изменения коэффициента теплоотдачи
разработана экспериментальная установка. Основной элемент установки –
герметичный теплообменник, через который прокачивается вода, отдающая тепло
испытуемым пластинам. Установка позволяет измерить в заданные моменты времени
τj значения температур
пластины Tj в месте установки термопары и в потоке
теплоносителя tc2.
Целью данной работы является расчёт среднего за
время эксперимента значения коэффициента теплоотдачи ![]() от потока
теплоносителя к поверхности пластины, выполненный на основе математических
моделей.
от потока
теплоносителя к поверхности пластины, выполненный на основе математических
моделей.
Углеродные нанотрубки (УНТ) «Таунит»,
производимые ООО «НаноТехЦентр», г. Тамбов, представляют собой длинные полые
волокна, состоящие из графеновых слоёв
фуллереноподобной конструкции.
Авторами [1] доказано, что дефекты углеродных
нанотрубок, являются центрами кристаллообразования металла покрытия в
электрохимических процессах. В местах дефектов нанотрубок атомы углерода
замещены кислородом, а при электрохимическом осаждении металлов, атомы
кислорода замещаются атомами металла. Морфология покрытия изменяется в сторону
значительного уменьшения межатомного расстояния в кристаллических группах
металла покрытия. Авторы заметили, что эту особенность, можно использовать
для получения уникального рельефа
покрытия.
В результате проведенных экспериментов
установлено, что добавка углеродных нанотрубок «Таунит» в раствор электролита
цинкования в количестве от 100 до 1000 мг/л позволяет получить специфический
микрорельеф гальванического покрытия, состоящий из выпуклостей с формой,
близкой к конической, высотой порядка 30-40 мкм (рис.1) и равномерной
плотностью распределения. Внутри каждого конуса находятся углеродные нанотрубки.
Количество конусов около 150-200 на 1 мм2.
В экспериментах применялись изделия из стали
Ст3. На поверхность изделий электрохимическим способом осаждался цинк. В стандартный щелочной электролит цинкования
углеродные нанотрубки вводились с помощью ультразвукового диспергатора.
Предварительные расчеты авторов, по результатам
экспериментов, показывают увеличение коэффициента теплоотдачи на 10-15%.
Исходными данными для расчёта являются:
- толщина пластины R1 и теплопроводность материала λ1,
из которого она изготовлена;
- толщина покрытия R2 и теплопроводность материала покрытия λ2;
- температура окружающей среды tc1;
- экспериментально полученные табличные значения
температур пластины Tj
в месте установки термопары и в потоке теплоносителя tc2, измеренные в известные
моменты времени τj;
- координата по толщине пластины места установки
термопары х0.

Рис.1.
Распределение мелкокристаллических образований УНТ «Таунит» на поверхности
цинкового покрытия.
В связи с наличием покрытия на поверхности
пластины, температурное поле экспериментального образца моделируется решением
задачи нестационарной теплопроводности для двухслойной неограниченной пластины
(индекс «1» относится к пластине, а индекс «2» - к слою покрытия):

![]() (1)
(1) ![]() (2)
(2)
![]() (3)
(3) ![]() (4)
(4)
![]() (5)
(5) ![]() . (6)
. (6)
Здесь ti(xi, τ)
– температурное поле двухслойной неограниченной пластины как функция поперечной
координаты и времени; ai2, λi
– соответственно, коэффициенты температуропроводности и теплопроводности
материала слоёв пластины; Ri
– толщины слоёв пластины; αi
– коэффициенты теплоотдачи от внешних поверхностей пластины; tci – температуры
окружающей среды.
Решение задачи (1) - (6)
имеет вид:
![]() . (7)
. (7)
Средние температуры по слоям равны:
![]() . (8)
. (8)
Вспомогательные
функции Qi, Pi, Zi,n, Tn, Nn,
входящие в решения (7) и (8), определяются
выражениями (9) – (22):
 (9)
(9) 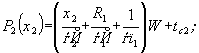 (10)
(10)
 (11)
(11) 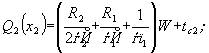 (12)
(12)
 (13)
(13) 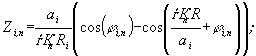 (14)
(14)
![]() (15)
(15)
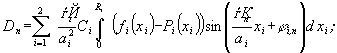 (16)
(16)
mn – последовательные
положительные корни уравнения
 (17)
(17)
 (18)
(18) 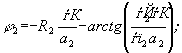 (19)
(19)
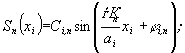 (20)
(20) 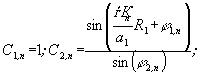 (21)
(21)
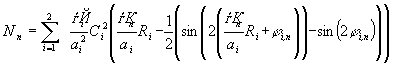 . (22)
. (22)
Собственные
числа mn задачи (1) – (6)
определяются как последовательные положительные корни уравнения (17). При
выполнении расчётов температурных полей необходимо вычислять первые N собственных чисел (N
– требуемое число членов ряда при использовании решений (7) и (8), определяемое
условиями сходимости).
При расчёте собственных чисел недопустим как пропуск корней, так и нахождение
решений, не являющихся корнями уравнения. Принимая во внимание требования к
надёжности, авторы применили метод дихотомии для поиска собственных чисел.
Работа
выполнена в рамках Федеральной целевой программы «Научные и научно-педагогические
кадры инновационной России» на 2009-2013 годы при поддержке Государственного
контракта № 14.740.11.1372.
Литература
1.
Литовка Ю.В., Дьяков И.А., Кузнецова О.А., Ткачёв А.Г., Попов Д.Ю., Столяров
Р.А. Технологии получения наномодифицированных гальванических покрытий. Нанотехнологии.
2011, №11 С.25-28