Лавріненко Н.М., Бескровний О.І.

Донецький національний університет економіки і торгівлі

імені Михайла Туган-Барановського

МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ РУЙНУВАННЯ БЛОКІВ

ЖИРУ У МАСЛОРІЗЦІ

Маючи математичну модель механічної поведінки жирів, можна моделювати процес їх обробки на технологічному обладнанні. Розрахунок за цією моделлю дозволить визначити параметри процесів і машин, оптимізувати їх за наявності певних конструктивних характеристик машин та режимів технологічного процесу.

Метою статті є обгрунтування реологічної моделі руйнування блоків жиру під дією динамічного навантаження у маслорізці пластифікатора ВВ-ПМЛ [1-2].

Жири мають коагуляційну структуру, це значить, що за умови малої зсувної напруги, що не перевищує межу плинності або граничну напругу зсуву, мають місце пружні, еластичні та пластичні властивості. Під час прикладення до жиру напруги, меншої за граничну напругу зсуву, у ньому миттєво виникає пружна деформація, що швидко зникає після зняття напруги. Еластична деформація поступово зростає до граничного значення, що залежить від прикладеної напруги, та поступово зменшується до нуля після зняття напруги. Пластична деформація та її швидкість визначаються прикладеною напругою і після зняття напруги пластична деформація припиняється у жирі. Вивчення експериментальних даних для жирів показує [3-4], що частина повної деформації, що зникає після зняття навантаження, звичайно, помітно менша, ніж пружна частина, яка виникає за умови прикладення напруги до продукту. Це явище можна пояснити на основі спеціально обраної реологічної моделі, яка складається з двох послідовно з'єднаних безінерційних пружин, а також безінерційного поршня, який переміщується з зазором у циліндрі, наповненому в'язкою рідиною з коефіцієнтом в'язкого опору переміщенню поршня . Внутрішня пружина прикріплена одним кінцем до поршня, а другим – до нерухомого дна циліндра. Зовнішня пружина розтягується або стискається силою та діє з тою ж силою на поршень (Рисунок 1).

Рисунок 1 – Реологічна модель жирів.

У такій моделі деформація та напруга задовольняють диференціальному рівнянню

, (1)

де - швидкість змінення напруги, - швидкість змінення деформації, - коефіцієнт інтенсивності релаксації, - час релаксації напруги при постійній деформації, , - коефіцієнт інтенсивності післядії, - час релаксації деформації при постійній напрузі, причому , очевидно, що >.

Жир є продуктом, який одночасно має властивості релаксації та властивості післядії. Під властивістю релаксації розуміють властивість тіла змінювати інтенсивність свого напруженого стану при незмінному деформованому стані, а під властивістю післядії – властивість тіла деформуватися після припинення змінення діючого на нього навантаження. Матеріал, деформування якого відбувається по лінійному закону (1), має і ту, і другу властивість [5]. Нехай блок (стрижень) жиру зазнає дії удару зі сторони маси (лопать шнека), яка рухається із початковою швидкістю . Якщо не враховувати власну масу блоку жира, то напружений і деформований стани по його довжині будуть однорідними.

Напруга у матеріалі при такому припущенні дорівнює

(2)

де - довжина блоку жиру, - площа перетину блоку, - переміщення правої сторони блоку.

Напруга та відносне подовження пружно-пластичного стрижня зв'язані рівнянням (1). З рівнянь (1) та (2) одержимо

(3)

У початковий момент часу відносне подовження та напруга дорівнюють нулю, тому початкові умови для диференціального рівняння (3) записуються у вигляді

(4)

Загальний інтеграл диференціального рівняння (3) має вид

(5)

де - корені характеристичного рівняння. Всі коефіцієнти в (5) додатні. Звідси витікає, що корені не можуть бути додатніми, а можуть мати місце тільки два випадки : 1) всі три корені від'ємні; 2) один корінь від'ємний, а два другі – комплексно спряжені. У обох розглянутих випадках виду коренів характеристичного рівняння відносне подовження, яке у початковий момент зростає, так як при , буде у подальшому спадати: або аперіодично, якщо всі корені характеристичного рівняння від'ємні; або у результаті згасаючих коливань маси, яка ударяє по пружно-пластичному стрижню. При цьому вважаємо, що маса після удару є зв'язаною зі стрижнем.

Після знаходження з рівнянь (4) величин можна знайти напругу як функцію часу:

(6)

Звідки маємо

(7)

де постійні визначаються рівняннями

(8)

а постійна визначається із умови рівності нулю напруги у початковий момент часу, тобто

(9)

Наявність у моделі двох пружин дає підставу припустити, що існують два види руйнації в'язко-пластичного матеріалу. Першому виду руйнації відповідає розрив зовнішньої пружини моделі. Цю руйнацію будемо називати зовнішньою – вона буде мати місце, коли напруга або на моделі розтягуюча сила буде більшою деякого граничного значення . Другому виду руйнації відповідає розрив другої (внутрішньої) пружини моделі. Розрив буде мати місце, коли > . Подовження внутрішньої пружини дорівнює , де - подовження першої пружини. Так як напруга у другій пружині дорівнює де , то її руйнація буде мати місце при виконанні умови .

Таким чином, руйнування блока жиру відбудеться, якщо виконується одна із умов:

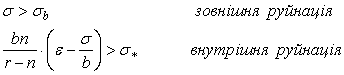(10)

Підставимо у (10) одержані значення (7) та (5). В результаті одержимо

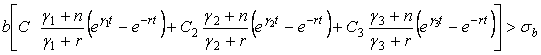(11)

Так як у вирази для коефіцієнтів швидкість ударяючої маси входить як множник, то при достатньо великому значенні швидкості обов'язково виконається одна із нерівностей (11) і наступить руйнування блока жиру.

Одержані розрахункові залежності напруги від швидкості ударяючої маси дозволяють визначити конструктивні характеристики механічного обладнання та параметри процесів, що пов'язані з руйнуванням блоків жиру в маслорізці ВВ-ПМЛ. Перспективами подальших досліджень є знаходження кількісних характеристик складових моделей та їх оптимізація.

Література

1. Пат. №82011 МПК (2006) B01F 7/02 A21C 1/00 A23P 1/10 A23G 1/10. Пластифікатор [Текст] / Литвин В.І. [та інш.] ; заявник і власник ТОВ «Фірма ВІ-ВА-ЛТД». – № а 2006 10227; заявл. 25.09.06; опубл. 25.02.08, Бюл. №2.– 6 с.

2. Пат. №21044 МПК (2007) С11В 5/00. Спосіб отримання пластифікованих масел і жирів [Текст] / Литвин В.І. [та інш.] ; заявник і власник ТОВ «Фірма ВІ-ВА-ЛТД». – № u 2006 10228; заявл. 25.09.06; опубл. 15.02.07, Бюл. №2.– 4 с.

3. Производство сливочного масла: Справочник [Текст] / Андрианов Ю.П., Вышемский Ф.А., Качераускис Д.В. и др., Под ред. д-ра техн. наук Вышемского Ф.А. . – М.: Агропроиздат, 1988. – 303с.- ISBN 5-10-000202-6.

4. Гуць В.С. Реологічні моделі харчових продуктів [Текст] / В.С. Гуць, О.А. Коваль // Харчова происловість.- 2000.- №45.- С.218-222.

5. Ишлинский А.Ю. Математическая теория пластичности [Текст]: монография / А.Ю. Ишлинский, Д.Д. Ивлев – М.: ФИЗМАТЛИТ, 2003.- 704с. – ISBN 5 – 9221 – 0141 – 2.