Математика /4. Прикладная математика/
Рябоштан А.Ф., Миленин А.Н.,
Федоренко В.Е.
Харьковский национальный
технический университет сельского хозяйства
имени П. Василенко
Конструирование
граничных поверхностей межлопаточного пространстваиз множества линий
Пусть задано n – параметрическое множество линий
![]() ,
, ![]() ,
, ![]() (1)
(1)
Поверхность
конструируется из множества линий (1) наложением (n–1) связей на параметр аi при помощи начальных условий, в качестве
которых выступают:
1. Кривая, с которой линии (1)
пересекаются.
2. Поверхность, с которой линии (1)
имеют касание І или ІІ порядка гладкости.
3. Линейная полоса, для которой линии
(1) пересекаются с кркивой – носителем полосы, а вточках пересечения касаются заданных
касательных плоскостей.
4. Полоса ІІ порядка.
Рассмотрим эти условия по
порядку:
1. Кривая m:
![]() ,
, ![]() ,
, ![]() (2)
(2)
Из условия пересечения с
кривыми множества при подстановке (2) в (1) позволяет получить два уравнения
связи параметров
![]() ,
, ![]() (3)
(3)
где общее количество параметров
увеличилось на 1 (прибавился u), а общее количество уравнений на 2,
так что из уравнений (3) можно получить уравнение связи параметров
![]() ,
, ![]() (4)
(4)
обеспечивающее персечение кривых
множества с кривой m. Для получения поверхности из (1)
необходимо иметь (n–1) таких связей u , следовательно, (n–1) начальных кривых в виде (2).
2. Пусть в качестве начального условия задана
поверхность
![]() (5)
(5)
Условие
перпендикулярности касательных к линиям (1) и нормалей поверхности (5) дает
дифференциальное уравнение:
 (6)
(6)
где ![]() ,
, ![]() ,
, ![]() – частные производные функции
– частные производные функции ![]()
Если из системы
уравнений (1), (5), (6) исключить координаты точки касания, получим одно
уравнение связи параметров:
![]() (7)
(7)
Следовательно для получения поверхности из множества (1) при соблюдении
касания I порядка
гладкости к заданным поверхностям необходимо иметь в качестве начальных условий
(n–1) поверхностей, которые позволяют
записать (n–1) уравнений (6), что совместно с (6) дает (n+1) уравнений, из которых нужно
исключить n
параметров. Для обеспечения второго порядка соприкосновения заданной
поверхности (5) и искомой необходимо вычислить частные производные ![]() по формулам:
по формулам:
 ,
,  ,
,
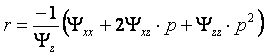 ,
,
 , (8)
, (8)
 ;
;
подставить их в уравнение (3), общее
для множества поверхностей, полученных из линий (6).
Совместное рассмотрение
(1), (5) и полученного уравнения после исключения x, y, z дает уравнение связи параметров:
![]() (9)
(9)
Уравнения (7) и (9)
гарантирует соприкосновение второго порядка гладкости. Указанное условие
рвносильно фиксированию двух параметров.
3. Рассмотрим начальное
условие в виде линейной полосы, т.е. кривой (2), в каждой точке которой заданы
координаты p и q нормали к искомой поверхности:
![]() ,
, ![]() (10)
(10)
Кривая
(2) приводит к двум уравнениям связи (3), а оснащение (10) – к уравнению,
аналогичному (6).
 (11)
(11)
Следовательно
каждая линейная полоса дает 3 уравнения связи, но вводит дополнительный
параметр u. Для
получения решения из множества (1) необходимо иметь ![]() полос, что имеет смысл
при нечетных
полос, что имеет смысл
при нечетных ![]() .
.
4.
Если начальные условия задачи в виде полосы второго порядка гладкости, т.е.
кривой (2), в каждой точке которой заданы частные производные
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (12)
(12)
удовлетворяющее условиям
полосы второго порядка гладкости, то для обеспечения второго порядка
соприкосновения искомой поверхности и полосы (12), необходимо, кроме двух
уравнений (3) для кривой и уравнения (11) для линейной полосы, составить ещё
одно уравнение, куда подставить (2) и (12). Таким образом, для получения
решения из множества (1) необходимо задать ![]() полос второго порядка
гладкости в виде начальных условий, что имеет смысл при
полос второго порядка
гладкости в виде начальных условий, что имеет смысл при
![]() ,
, ![]() (13)
(13)
При
решении практических задач из множества (1) можно получить различные
поверхности, изменяя количество и вид начальных условий. Например, при ![]() можно взять две
линейные полосы и одну кривую или одну полосу, две кривые и одну касательную
поверхность и т.д. Общее число
можно взять две
линейные полосы и одну кривую или одну полосу, две кривые и одну касательную
поверхность и т.д. Общее число ![]() параметров множества
(1), способного реализовать заданные начальные условия, равно:
параметров множества
(1), способного реализовать заданные начальные условия, равно:
![]() , (14)
, (14)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - число кривых полос первого и
второго порядков гладкости, поверхностей с условием касания и соприкосновения
второго порядка соответственно
- число кривых полос первого и
второго порядков гладкости, поверхностей с условием касания и соприкосновения
второго порядка соответственно
![]() , (
, (![]() ,
, ![]() )
)
При
практической реализации рассмотренных выше вопросов следует учитывать условия
непротиворечивости задания начальных условий, накладывающие ограничения на
взаимное расположение геометрических элементов.
Конкретные
расчетные алгоритмы должны быть увязаны с обобщенным алгоритмом дифференциально-параметрического
метода и отражать условия ипнциндентности и касания заданного порядка.