НЕЧЕТКИЕ ГРАФ-СХЕМЫ.

Айпанов Ш.А., Мерембаев Т.Ж.

Казахский Национальный Университет имени аль-Фараби

Четкие граф-схемы рассматриваются в работах [1,2]. Мы обобщим понятие граф-схемы применительно к теории возможностей и теории нечетких множеств.

Рассмотрим функцию, ставящую в соответствие каждому вектору из пространства нечетких описаний N признаков нечеткий граф с вершинами из множества E:

Причем, потребуем выполнения следующих условий.

1. Множество вершин E состоит из N+1 непересекающихся подмножеств:

,

Каждое при соответствует признаку : вершины из «проверяют» признак . Множество состоит из одной вершины . есть множество классов: .

2. При любом значении

a. Вершина S - начальная:

b. Дуги, исходящие из входят в вершины :

c. Вершины - конечные

Таким образом, суть N+1 хроматический граф [3].

3. Вес дуги, исходящей из вершины и входящей в вершину , определяется некоторым нечетким множеством , связываемым с A и B:

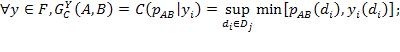
Подобную функцию мы будем называть нечеткой граф-схемой возможностей и изображать в виде графа с вершинами, связанными взвешенными величинами дугами, как показано на рис. 1.

Рис. .1. Дуга граф-схемы

Нечеткая граф-схема необходимостей вводится, как функция, ставящая в соответствие нечеткий граф дополнение которого удовлетворяет перечисленным выше условиям. Т.е. дополнение нечеткой граф-схемы необходимостей есть нечеткая граф-схема возможностей, веса дуг которой являются дополнениями весов соответствующих дуг в исходной граф-схеме.

Граф-схемой вообще, мы будем называть пару нечетких граф-схем - возможностей и необходимостей:

Мы будем говорить, что дуга в граф-схеме возможностей отсутствует, если ее вес - пустое подмножество D_i. Аналогично, в граф-схеме необходимостей дуга опускается, если ее вес есть .

Можно отметить аналогию, между граф-схемой возможностей и электрической схемой, составленной из сопротивлений, с одной стороны, и, между граф-схемой необходимостей и электрической схемой из проводимостей, с другой.

Преимущества использования нечетких граф – схем являются удобное средство представления нечетких классификаторов. Для машинной реализации разумно использовать граф-схемы в канонической форме - с четкими дугами. Алгоритм построения граф-схемы реализует нечеткое правило ближайшего соседа.

СПИСОК ЛИТЕРАТУРЫ

1. Танаев В.С., Поварич М.П. Синтез граф-схем алгоритмов выбора решений / Под ред. А.Д.Закревского.- Минск: Наука и техника, 1974.- 112с.

2. Блох А.Ш. Граф-схемы и алгоритмы.- М.:Высш.шк., 1987.- 144с.

3. Кристофидес Н. Теория графов, алгоритмический подход. – Мир, 1978. – 432с.