Калижанова У.С., Курлапов Л.И.

Казахский национальный университет им. Аль-Фараби, Алматы

Расчеты теплоемкости газов умеренной плотности на основе кластерной модели

Экспериментальные данные по температурной и барической зависимости теплоемкостей газов говорят о том, что такие зависимости носят нерегулярный характер [1]. В частности, температурная зависимость различных газов имеет различный вид. Для каждого газа при различных давлениях вид температурной зависимости различный: если в одной области давлений удельная теплоемкость может расти с температурой, то в другой области давлений она может убывать. Такое многообразие не удавалось описать теоретически.

В данном докладе получены формулы для расчетов удельной теплоемкости и приведены результаты расчетов, которые хорошо описывают известную температурную зависимость удельной изобарной теплоемкости, что продемонстрировано на примере азота. Описание проведено на основе обобщенного термодинамического соотношения Гиббса, в котором образование структур в виде кластеров учитывается специальным потенциалом структурности и связанной с ним координатой структурности [2].

В кластерной модели каждый газ рассматривается как многокомпонентная смесь молекул и кластеров различных размеров: димеров, тримеров и.т.д. [3]. В настоящем докладе рассмотрен азот умеренной плотности, который представляет собой молекулярно-кластерную смесь: он состоит из молекул одного сорта и из различных кластеров, которые состоят из этих же молекул. В рамках великого статистического ансамбля [2] соотношение Гиббса для одного моля такой смеси записывается так:

,

где – температура, – энтропия, – давление, – объем, – потенциал структурности одного моля, – координата структурности (молярная синергия), – размер кластера в числах входящих в него молекул (для молекул принимается =1), – размер наибольшего кластера, который существует в данной системе при данных условиях.

Это соотношение дает следующие соотношения для молярных теплоемкостей молекулярно-кластерной смеси:

,

где – числовая доля (концентрация) кластерного субкомпонента,

– молярная теплоемкость при постоянном давлении.

В этом выражении молярная теплоемкость молекулярно-кластерной смеси представлена в виде двух частей. Первая часть – это так называемая замороженная теплоемкость и вторая часть, аналогичная реакционной составляющей в чисто молекулярных системах с диссоциациями, в данном случае – структурная. Замороженная теплоемкость находится по обычным правилам, по которым находится теплоемкость смеси. Структурная часть теплоемкости зависит от эволюции кластерного состава при изменении температуры, количественной мерой которой служит производная от концентрации по температуре. Для частиц, которые образуются при повышении температуры потенциал структурности отрицательный (при образовании частиц поглощается энергия кластерообразования). В газах обычно можно выделить доминирующие кластеры, концентрация которых достаточно высока, и они в связи с этим вносят наибольший вклад в теплоемкость как в замороженную, так и в структурную. Во многих случаях к доминирующим кластерам относятся молекул (как одномерные кластеры) и они дают положительный вклад в структурную часть общей теплоемкости всей молекулярно-кластерной смеси.

В измерительной практике удобнее использовать удельную теплоемкость. Удельная теплоемкость молекулярно-кластерной смеси определяется обычным образом:

,

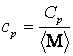где – молярная масса молекулярно-кластерной смеси, которая существенно зависит от кластерного состава:

,

где – молярная масса молекулярного субкомпонента, приведенная для всех веществ в таблице Менделеева.

Из приведенных соотношений видно, что теплоемкость содержит несколько составляющих, причем значения различных составляющих существенно зависят от кластерного состава и от его эволюции, которые в свою очередь зависят от давления и температуры. Этим объясняется наблюдаемые изменения теплоемкости. На рисунке 1 для примера приведены результаты расчетов удельной изобарной теплоемкости азота. Сравнение с известными экспериментальными данными показывают хорошее совпадение расчетов с экспериментом.

Рис. 1. Температурная зависимость удельной изобарной теплоемкости азота при давлении 5.0 МПа. Сплошная линия – расчеты, пунктирная линия – табличные данные [1]

Как видно из формул, для вычисления теплоемкости необходимо знать кластерный состав и его эволюцию при изменении температуры. Концентрации кластеров и их производные по температуре рассчитывались по схеме, основанной на экспоненциальном распределении кластеров по размерам [3]. На рисунке 2 приведены данные по кластерному составу азота при давлении 5.0 МПа при некоторых температурах. Эти данные использованы и для определения производных от концентрации по температуре.

Рис. 2. Распределение концентраций кластеров по размеру

Литература

1 Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука. 1972.- 720 с.

2 Курлапов Л.И. Иерархия статистических ансамблей и энтропийно - синергийный анализ сложных систем. // Доклады Министерства науки - Академии наук Республики Казахстан. 1996- №5 . стр. 34-37.

3 Курлапов Л.И.Кластерная модель газа// ЖТФ.- 2003. – Т. 73, вып. 2.- С 51-55.