Промышленная экология и медицина труда

Буртная И.А., Литвиненко Д.В.

Национальный технический Университет Украины «КПИ»

Математическое моделирование

процесса первапорации (Часть 2)

Аннотация

В работе представлены граничные условия для математической модели процесса первапорации бинарных смесей.

Вступление

Для описания и анализа процесса первапорации необходимо математическое моделирование, которое в свою очередь невозможно без задания граничных условий. Дадим описание рассматриваемой системы. Первапорация происходит в канале прямоугольного сечения. Отдельный компонент смеси проходит через мембрану, сначала растворяясь в ней, происходит фазовый переход, а потом испаряется с внешней стороны мембраны в паровую фазу [1].

Граничные условия

Для системы уравнений, составляющих математическую модель процесса, требуется задать граничные условия.

Граничные условия определены при , , и . Считаем, что на входе в канал () профиль скорости имеет параболический вид:

,

полагая, что образовался профиль полностью развитого ламинарного течения. На входе в мембрану концентрации растворенного вещества и растворителя – и соответственно, а температура и давление на входе в канал были установлены равномерными (величины T₀ и p₀ соответственно). Выше записанные условиях при были выражены в безразмерной форме, как

; ; ; ; .

Отметим, что на выходе так же, как и входе, можно использовать альтернативный набор граничных условий для массо- и теплопереноса, что отвечает диффузии и конвекции:

;

; (1)

,

где на входе в канала (), и , где обозначает компоненту или .

На поверхности мембраны () применяется обычное условие прилипания на границе, то есть при , которое соответствует первапорации для непористых мембран. Составляющая скорости по -координате может быть выражена как:

при и при , (2)

где , (3)

где компоненты потока пермеата можно выразить как:

, (4)

в котором и – -тые концентрации компонентов в мембране – на поверхности входа в мембрану и на границе мембрана-пермеат соответственно; - сопротивление мембраны массопереносу -тых компонентов. При условии наличия незначительного вакуума со стороны пермеата, разумно предположить, что . Кроме того, если предположить, что на стороне входа в мембрану существует локальное термодинамическое равновесие, то получим, что концентрации компонентов в растворе связанны с их концентрациями в мембране (при ), таким образом, что . Тогда уравнение (3) может быть выражено как:

,

где и - коэффициенты массосопротивления мембраны для компонентов и соответственно могут быть определены как , где - коэффициент массопереноса для «транспорта» через мембрану и - это коэффициент распределения мембрана/раствор для -тых компонентов. В данном моделировании сопротивление мембраны аппроксимировалось как , где - толщина мембраны и - коэффициент диффузии -того компонента внутри мембраны. Температурная зависимость диффузии и коэффициентов распределения может быть аппроксимирована как:

; ,

где и - энергия активации диффузии и энтальпия растворения -того компонента в мембране соответственно, а и - соответствующие предэкспоненциальные множители.

На поверхности мембраны со стороны потока ( и ) предполагаются следующие граничные условия для системы уравнений переноса массы:

; , (5)

где члены правой стороны системы уравнений (5) представляют компоненту потока (согласно (4)).

Граничные условия теплопереноса на поверхности мембраны могут быть выведены из теплового баланса, который учитывает как заметный теплоперенос, так и теплоты парообразования. Соответственно, может быть получено следующее граничное условие [3]:

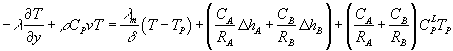, (6)

где - теплопроводность мембраны, - температура пермеата, и - энтальпии испарения компонентов и соответственно, и - теплоемкость пара пермеата. Выше предложенное граничное условие теплоотдачи (6) может быть выражено в безразмерном виде, как [2]

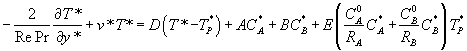, (7)

где

; ;

; .

Выводы

В связи с малой изученностью процесса первапорации проведение исследований следует продолжать.

Стоит задача моделирования процееса первапорации бинарной смеси в канале круглого сечения и соответственно дополнения этой модель граничными условиями. Также следует провести расчет полученной математической модели и анализ его результатов.

Литература

1. І.А.Буртна, Д.В.Литвиненко. Мембранна технологія очистки стічних вод від органічних домішок // Східно-Європейський журнал передових технологій / Екологія, 2010. – 6/10(48).– с.4-6.

2. Juan P.G. Villaluenga, Yoram Cohen. Numerical model of non-isotermal pervaporation in a rectangular channel / Journal of membrane science. – 2005. – 260. – p.119-130.