Новикова О.Н., Рындина А.А.

Донецкий национальный университет экономики и торговли имени Михаила Туган-Барановского, Украина

ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИЧЕСКИХ РАСЧЁТАХ

Понятие матрицы чрезвычайно важно для экономистов, т.к. благодаря этому значительная часть математических моделей экономических объектов и процессов записывается в компактной и достаточно простой матричной форме. Одним из преимуществ матричной формы записи является то, что в малом наборе символов объединено множество математических операций. Благодаря этому, матричная форма записи очень удобна и полезна при анализе данных, необходимость которого возникает всё чаще, в связи с распространением количественных методов исследований в экономической теории и коммерческой деятельности. Матричная форма записи часто оказывается полезной, когда нужно использовать математические методы исследования. Она облегчает как организацию необходимых расчётов, так и понимание этих операций. Целью данной работы является исследование матричных моделей, применяемых в экономике.

В матричных моделях отражается структура затрат на производство и распределение продукции. Балансово-нормативные матричные модели объединяют в единой табличной форме балансы распределения продукции по отдельным её видам и связанные с ними балансы затрат на производство, а также нормативы денежных затрат. Матричные модели используются для плановых расчётов с применением электронной вычислительной техники и экономического анализа, также они используются для нахождения прямых затрат, приращения валового выпуска, объёма продаж, прироста продаж, объёма производства и т.д.

С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:

Ресурсы	Отрасли экономики
	Промышленность	Сельское хозяйство
Электроэнергия	5,3	4,1
Трудовые ресурсы	2,8	2,1
Водные ресурсы	4,8	5,1

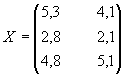
В данной записи, например, матричный элемент а₁₁=5,3 показывает, сколько электроэнергии употребляет промышленность, а элемент а₂₂=2,1 – сколько трудовых ресурсов потребляет сельское хозяйство.

Широко известна описанная в 1936 г. американским экономистом В.В. Леонтьевым основная модель макроэкономики.

Предполагается, что для производства единицы продукции j-той отрасли требуется определённое количество затрат промежуточной продукции i-той отрасли, равное aij. Оно не зависит от объёма производства в отрасли и является довольно стабильной величиной во времени. Величины aij называются коэффициентами прямых материальных затрат и рассчитываются следующим образом: aij = xij / хj , (i,j = 1, 2,...,n). Итак, коэффициент прямых материальных затрат показывает, какое количество продукции i-той отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j-той отрасли. С учётом формулы систему уравнений баланса можно переписать в виде: Хi = (ai1 x1 + ai2 x2 + ... + ain xn) + Yi , (i = 1, 2,...,n).

Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А, вектор-столбец валовой продукции X и вектор-столбец конечной продукции Y:

то система уравнений в матричной форме примет вид: X=AX+Y. Данное уравнение и называется моделью Леонтьева. Его можно использовать в двух целях.

В первом случае по известному вектору валовой продукции Х требуется рассчитать вектор конечной продукции Y. Переписываем последнее уравнение в виде: Х ⋅ (Е – А) = Y.

Во втором случае, если матрица (Е – А) невырожденная, т.е. , то по известному вектору конечного потребления Y можно определить вектор валового выпуска Х, по формуле: .

Таким образом, в работе показаны преимущества использования матричных моделей, рассмотрена основная модель макроэкономики. Проанализировав использование матриц в экономике, мы пришли к выводу, что достоинства матриц состоят в том, что они используют широкий выбор стратегически значимых переменных, указывают направление движения ресурсов, также позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные. Таким образом, умение оперировать матрицами полезно в решении реальных экономических задач.