Математические науки. Дифференциальные и интегральные
уравнения
Ахажанов Т.Б.
Евразийский национальный университет им.
Л.Н. Гумилева, г. Астана
ВАРИАЦИОННЫЙ МОДУЛЬ
НЕПРЕРЫВНОСТИ И КОЭФФИЦИЕНТЫ КРАТНЫХ РЯДОВ ФУРЬЕ-ХААРА.
В данной работе приводятся условия сходимости рядов,
составленных из коэффициентов Фурье-Хаара функций ограниченной p- вариаций.
Определения. Пусть функция ![]() определена на
множестве
определена на
множестве ![]() и
и ![]() , где
, где ![]() ,
, ![]() ,
, ![]() - произвольное разбиение множества
- произвольное разбиение множества ![]() . Вариационной суммой порядка
. Вариационной суммой порядка ![]() функции
функции
![]() по разбиению
по разбиению ![]() назовем величину
назовем величину
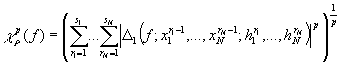 ,
,
где
![]() ,
,
![]() и
и ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Для функции одной переменной понятие вариационной
суммы впервые ввел Винер [1], для функций двух переменных
-Л.Кларксон и С.Адамс [2].
Вариационным модулем непрерывности ![]() порядка
порядка ![]() функции
функции ![]() называется величина
называется величина
![]()
где ![]() . Будем говорить, что
. Будем говорить, что ![]() ,
, ![]() , если
, если ![]() , и что
, и что ![]() ,
, ![]() , если
, если ![]() . Свойства
вариационного модуля непрерывности для функции одной переменной исследованы
А.П. Терехиным [3], С.С. Волосивецем [4].
. Свойства
вариационного модуля непрерывности для функции одной переменной исследованы
А.П. Терехиным [3], С.С. Волосивецем [4].
Функции
системы Хаара на ![]() задаются так:
задаются так: ![]() при
при ![]() ; если же
; если же ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
,
то
 .
.
Пусть ![]() ,
, ![]() -параметр суммирования,
-параметр суммирования, ![]() ,
, ![]() ,
,
тогда кратную систему
Хаара определим следующим образом:
![]() .
.
В данной работе исследуется
вопрос: при каких условиях, накладываемых на
вариационный модуль непреррыности ![]() порядка функций многих переменных
имеет место сходимость ряда
порядка функций многих переменных
имеет место сходимость ряда
![]() ,
, ![]() ,
,
где ![]() -коэффициенты Фурье-Хаара функции
-коэффициенты Фурье-Хаара функции ![]() . Для случай функций одной переменной такие вопросы
рассматривались С.С. Волосивецом [6].
. Для случай функций одной переменной такие вопросы
рассматривались С.С. Волосивецом [6].
В
следующей теореме приводится оценка коэффициентов Фурье-Хаара функций многих
переменных через вариационный модуль непрерывности порядка ![]() .
.
Теорема 1. Пусть ![]() ,
, ![]() и
и
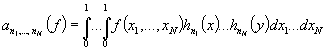 ,
, ![]() .
.
Тогда верно неравенство
 .
.
Теорема 2. Пусть ![]() ,
, ![]() и
и
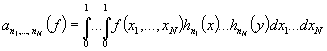 ,
, ![]() .
.
1) Пусть ![]() ,
, ![]() . Тогда при условии сходимости ряда
. Тогда при условии сходимости ряда

сходиться ряд
![]() .
.
2) Пусть ![]() ,
, ![]() ,
, ![]()
![]() . Тогда при условии сходимости ряда
. Тогда при условии сходимости ряда

сходиться ряд
![]() .
.
Литература
1. N.Wiener. The
quadratic variation of a function and its Fourier coefficients / Massachusetts
J.Math., 3(1924), 72-94 с.
2.
J.A. Clarkson and C.R. Adams. On definitions of bounded variation for functions of
two variables /
Trans. Amer. Math. Soc., 35(1933),
824-854 с.
3.
Терехин А.П. Приближение
функций ограниченной p- вариации /
Изв. Вузов. Математика. 1965. №2. 171-187 с.
4.
Волосивец С.С.
Приближение функций ограниченной p- вариации
полиномами по системам Хаара и Уолша / Мат. Заметки. 1993. Т 53. №6. 11-21 с.
5.
Б.И.Голубов, А.В.Ефимов,
В.А.Скворцов. Ряды и преобразования Уолша: теория
и применения. /
Москва «Наука», 1987 г.