УДК 532.543

 

РЕШЕНИЕ ЗАДАЧИ УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ

ИДЕАЛЬНЫХ ДВУХФАЗНЫХ СРЕД В ОТКРЫТЫХ КАНАЛАХ

ПЕРЕМЕННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

 

Нысанов Е.А., Каратаев Г.С.

Южно-Казахстанский государственный университет им. М.Ауезова

Республика Казахстан, г. Шымкент

 

Остановимся на параметрах твердых фаз. Как известно, коэффициент Шези зависит от гидравлического сопротивления. Полное сопротивление, оказываемое движению естественным руслом, слагается из трех частей: сопротивление зернистой шероховатости дна, сопротивление макрошероховатости, т.е. донных гряд и рифелей, и сопротивление формы русла. Под последним понимается сопротивление, вызванное изменением площади живых сечений потока, т.е. в конечном счете, потерями при переходе кинетической энергии в потенциальную. Практическое значение эти потери приобретают в местах резкого расширения русла. Ограничиваясь двумя первыми видами сопротивления, используем более общую формулу коэффициента Шези [1].

  ,

где  ;    ;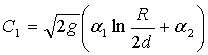

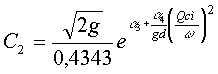d – средний диаметр твердых частиц;

Qсм – расход смеси;

1, 2, 3, 4-экспериментальные коэффициенты.

Исследования ряда авторов показывают, что неравномерность распределения концентраций по глубине влияет на сопротивление движению. Поэтому при совместном движении воды и твердых частиц это распределение играет важную роль. Для распределения концентрации твердой фазы используем следующее выражение:

                                                                                 (1)

где  f20 – концентрация твердой фазы у дна (у=0);

Н – глубина потока;

U – средняя скорость потока;

m1 – коэффициент, равный по Буссинеску 22,3, по Базену 24;

uк – гидравлическая крупность.

Многочисленными исследованиями отечественных и зарубежных ученых установлена связь между диаметрами частиц наносов и их гидравлической крупностью. Следует отметить работу В.Н. Гончарова, давшего эмпирические формулы гидравлической крупности, обобщающие экспериментальные материалы других исследований. Он выделил три характерных режима осаждения:  ламинарный, переходной, турбулентный и для каждого дал особую формулу гидравлической крупности: для ламинарного режима

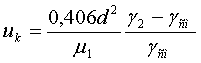(d=0,00001-0,00015 м),

для переходного

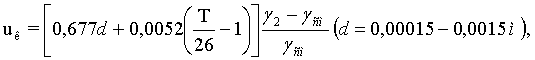
для турбулентного

Здесь  -коэффициет вязкости воды;

 - удельный вес твердой частицы;

 - удельный вес смеси;

T – температура жидкой фазы.

Расходы определяются по формулам:

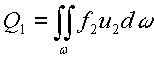                              ;  ;                             (2)

,

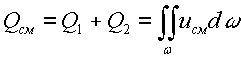где  -  продольная скорость смеси;

 - концентрация жидкой фазы.

Удельный вес твердой частицы, связанный с ее минералогическим составом, и геометрический размер, который обычно выражают через ее средний диаметр, являются важными характеристиками наносов. Размеры зерен донных наносов в значительной степени характеризуют шероховатость русла. С другой стороны, от геометрических размеров частиц зависит способность их перемещения по дну при тех или иных скоростях течения. Удельный вес речных наносов обычно составляет от 2000 до 2800 кг/м3.

Поставленная  задача  решается  исходя из  «взаимопроникающей» модели  двухфазных  сред, согласно  которой  уравнений  движения  имеют  вид [2,3]:         

             (3)

 и  уравнение  неразрывности 

                          

где   - приведенная  и  истинная  плотности  n-й  фазы  соответственно,

 - продольная  составляющая  скорости  n-й  фазы;

- вертикальная  составляющая  скорости  n-й   фазы;

 - концентрация (обьемное содержание ) n-й  фазы;

P – давление;

 - коэффициент  вязкости n-й фазы;

К- коэффициент  взаимодействия  между фазами;

 - компоненты массовой силы n-й фазы;

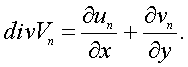
   Рассмотрим   случай  установившегося одномерного  течения  идеальных  двухфазных  сред  в открытых  каналах. При  этом  считаем, что  обе  компоненты несжимаемы  и  массовой  силой  можно  пренебречь. Тогда  уравнений  движения (3) для  рассматриваемого  случая  имеют   вид:         

 

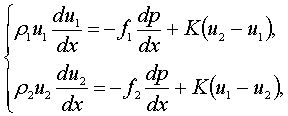                                                             (4)

 

а  уравнение  неразрывности  в  силу  постоянства  расхода  и  согласно  формулам   (2)

                                                                                       (5)

где  -  площадь живого  сечения,  для различных  каналов  задаются  различными  формулами.

Систему (4), (5)  можно  написать  в следующем виде:

 

                                                         (6)

 

где с1,с2 – постоянные, произведения приведенных плотностей, скоростей соответственно первой и второй фазы и площади живого сечения канала во входном створе, т.е.  . При этом во входном створе для концентрации твердой фазы используем формулу (1), вводя обозначения  и  и вычитая из первого уравнения системы (6) второе уравнение, имеем

 

,   (7)

 

где  - производная  по х

 

из последних трех уравнений системы (6) находим:

    ,

 

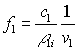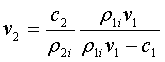                                             ,                                     (8)

 

  

Решая совмесно системы уравнений (7) и (8) можно найти выражения для скорости  и концетраций  первой и второй фазы.

 

 

 

Литература

1.     Абальянц С.X. Устойчивые и переходные режимы в искусственных руслах. Л.: Гидрометеоиздат, 1981. –238 с.

2.     Шаюсупов М. Движение многофазных потоков с переменным расходом в руслах. Отв. ред. Х.А. Рахматулин. Ташкент, Фан, 1981, –163 с.

3.     Умаров А. И., Ахмедов Ш.Х. Двумерные задачи гидродинамики многофазных сред - Ташкент: Фан, 1989. –96 с.