Сарсенби А.М ., Сапарбаева Э.М.

ЮКГУ им М.Ауезова, г. Казахстан

Свойства вектор – функций оператора Шредингера с матричным потенциалом.

Дифференциальные операторы вида

,

заданные в пространстве вектор - функций, с матричным потенциалом были рассмотрены в работе , где была развита теория базисности В.А.Ильина . При этом корневые функций оператора были определены по формулам

Как известно , в случае скалярного оператора , при таком определении присоединенных функций возникает проблема выбора присоединенных функций. Указанная проблема выбора присоединенных функций исчезает , если присоединенные функции определить по формуле

Поэтому, естественно исследовать свойства собственных и присоединенных функций оператора при таком определении.

Пусть гильбертово пространство комплекснозначных вектор – функций состоящих из компонентов. Скалярное произведение элементов этого пространства определяется равенством

,

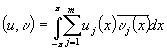где . Тогда норма элемента может быть определена равенством

Собственные и присоединенные функции оператора будем понимать в обобщенном смысле В.А.Ильина. Пусть вектор – функции абсолютно непрерывны вместе со своими первыми производными на промежутке и почти всюду на этом отрезке удовлятворяют матричным уравнениям.

(1)

где - диагональная матрица, - число, равное либо нулю, либо единице, причем =0. При =0 вектор – функцию называем собственной функцией. При =1 дополнительно требуем и вектор функцию называем присоединенной функцией.

Обозначим , , и будем считать что число занумерованы в порядке возрастания их абсолютных величин.

Справедлива следующая

Теорема. Пусть каждый элемент потенциала принадлежит классу и . Тогда для собственных и присоединенных функций оператора выполняются следующие оценки:

.

Для любых двух точек , отрезка и для любой присоединенной функции оператора имеет место следующая формула среднего значения

Полагая перепишем эту формулу для случая знака + .

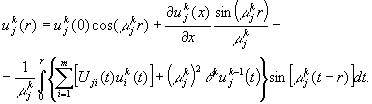(2)

Будем считать, что . Так как , ограничены при из (2) получаем

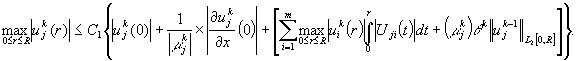
Все элементы потенциала принодлежат . Учитывая это и суммируя обе части последнего неравенства по всем от 1 до , получим

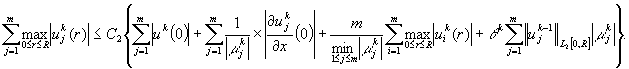
При достаточно больших значениях параметра из полученного неравенства вытекает оценка

(3)

Два первых слагаемых в правой части (3) оцениваются изложенным способом с помощью формулы (2) путем умножения этой формулы соответственно на и и последующим интегрированием полученного соотношения по переменной в пределах от 0 до . При этом учитывается тот факт, что ,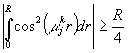

В результате этих действий, будем иметь:

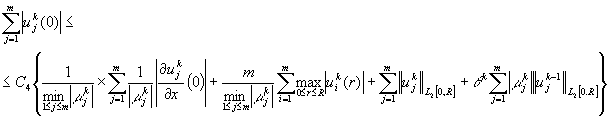(4)

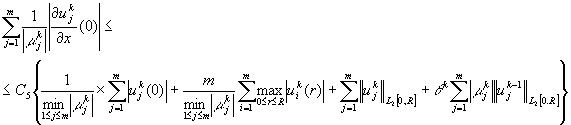(5)

Сопоставляя (4) и (5) получим,

(6)

(7)

Два первых слагаемых в правой части (3) оценим с помощью соотношений (6) и (7), которые справедливы для любого . Эти обстоятельства позволяет написать неравенство (3) в виде

(8)

Совершенно аналогично уставливается такая оценка для левой половины рассматриваемого отрезка:

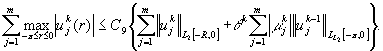(9)

Объядиняя оценки (8) и (9) получаем

Это значит

Теорема доказана.

Литература

1.Куркина А.В. О базисности Рисса корневых вектор – функций оператора Шредингера с матричным потенциалом и матричным спектральным параметром // Дифференц. уравнения. 1994., Т.30., №6. С. 972-986.

2.Ильин В.А., Мальков К. В., Моисеев Е. И. // Дифференц. уравнения. 1989. Т. 25, № 12. С. 2133-2143.

3. Садыбеков М.А; Сарсенби А.М. К теории оценок антиаприорного тила в смысле В.А. Ильина // Доклады РАН.2008., Т.420, № 3. С. 316-319.