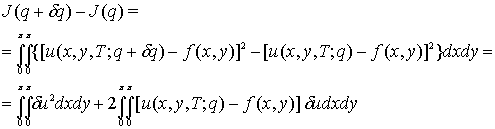Математика/5. Математическое моделирование

к.ф-м.н. Д.Б. Нурсеитов, докторант PhD А.Н. Алимова

Казахский национальный педагогический университет им. Абая,

Алматы, Казахстан

Решение обратной задачи Дирихле двумерного волнового уравнения

1. Постановка задачи

Работа посвящена численному исследованию задачи Дирихле для волнового уравнения. Задача рассматривается в прямоугольной области. Рассмотрим постановку прямой задачи:

В обратной задаче требуется найти , по дополнительной информации относительно решения прямой задачи (1) – (5)

Решаем задачу минимизацией целевого функционала

минимизировать который будем методом итераций Ландвебера

при

2. Вычисление градиента функционала

Рассмотрим функционал (7) в следующем виде

Найдем приращение функционала

Рассмотрим задачу на

Рассмотрим тождественно равное нулю выражение, вытекающее из (11)

Рассмотрев выражение, сформулируем постановку сопряженной задачи, вытекающее из (16)

получаем выражение:

Откуда, учитывая (14), из (22) получаем выражение для градиента функционала

3. Численные результаты

Алгоритм метода итераций Ландвебера

1. Задаем параметр спуска .

2. Для известного точного решения находим дополнительную информацию , решая прямую задачу берем след решения.

3. Задаем начальное приближение .

4. Предположим, что уже известно, тогда решаем прямую задачу (1) – (5).

5. Считаем .

6. Если текущее значение функционала - мало, то решаем сопряженную задачу (17) – (21) .

7. Вычисляем градиент функционала

8. Вычисляем следующее приближение , где .

Схема решения прямой задачи

Запишем задачу (1) – (5) в конечно – разностном виде. Пусть – количество узлов равномерной сетки на интервале , а – количество узлов равномерной сетки на интервале . Определим шаг сетки: .

Решив задачу получаем след решения

Описание численного эксперимента

Расчеты тестовой задачи проводились для , , , , параметр спуска – , точное решение которой известно:

начальное приближение:

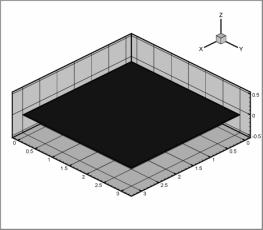
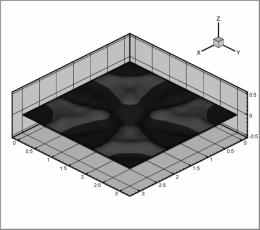
Рис. 1: График функции	Рис. 2: График функции
Рис. 3: График функции	Рис. 4: График функции

Рис. 5: График функционала	Рис. 6: График

Литература:

1. Бурский В.П. Методы исследования граничных задач для общих дифференциальных уравнений. - Киев: Наукова думка, 2002.

2. Пташник Б.И. Некорректные граничные задачи для дифференциальных уравнений с частными производными. - Киев: Наукова думка, 1984.

3. Кабанихин С.И. Обратные и некорректные задачи. - Новосибирск: Сибирское научное издательство, 2009.

4. Кабанихин С.И., Бектемесов М.А., Нурсеитова А.Т. Итерационные методы решения обратных и некорректных задач с данными на части границы. - Алматы-Новосибирск: ОФ «Международный фонд обратных задач», 2006.

5. Владимиров В.С. Уравнения математической физики. - Москва: Наука, 1988.

6. Тихонов А.Н., Самарский А. Уравнения математической физики. - Москва: Наука, 1972.