MONASHOVA
A.Z.
ABOUT SPECTRUM OF ONE DIFFERENTIAL OPERATOR, ASSOCIATED WITH
QUADRATIC FORM
L.N.GUMILYOV
EURASIAN NATIONAL UNIVERSITY
In this paper we consider operator 
, associated
with differential expression
, 
(1)
where 
, 
is the class of infinitely differentiable and
finite functions on 
, 
are non negative functions
with absolutely continuous derivatives 
, 
is a non-negative locally integrable
function on 
this conditions:
. (2)
Let 
. We assume
,
where 
, 
is the set of all measurable
sets 
with measure 
.
From properties of absolutely
continuity of measure 
it follows that there exists sufficiently small number
, such that
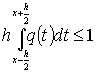, if 
.
Therefore for all 
the following
estimates hold
,
.
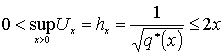We introduce 
if 
,
,
,
is the inverse of function 
.
Òheorem 1 Let the following conditions hold:
1. 
and 
,
2. 
and 
.
Then the operator 
has a discrete spectrum
and the following estimates hold
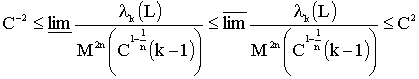. (3)
Remark. The problem about discrete spectrum of operator
generated by a common differential expression was posed in /1, §1.1/. The
function 
is “Otelbaev average”.
References
1. Otelbaev Ì.Î. Estimates of spectrum
of Sturm-Liouville operator. – Alma-Ata: Gylym, 1990. – 191c.