Секция: Математика; подсекция: Математическое моделирование

Лавриненко Н.М., Дахов А.Г.

Донецкий национальный университет экономики и торговли

им. М.И.Туган-Барановского

МОДЕЛИРОВАНИЕ ПРОЦЕССА ДИФФУЗИИ ДЛЯ ОБЪЕКТОВ СЛОЖНОЙ ГЕОМЕТРИИ

В настоящее время важное место в инженерной деятельности занимает исследование процессов диффузии. На практике часто необходимо знать как происходит распределение влаги в каком либо веществе (продукте, полимерном материале и т. д.) с течением времени и в зависимости от параметров среды, которая окружает исследуемое вещество.

В данной работе исследуется сушка слоя неоднородного вещества. Слой имеет каналы (поры), которые заполняет воздух. До сушки слой имеет относительную влажность 80%. Необходимо определить, какой вид будет иметь распределение влажности в каждый момент времени в системе на протяжении всего процесса сушки, при условии, что конечный продукт должен иметь относительную влажность 10% .

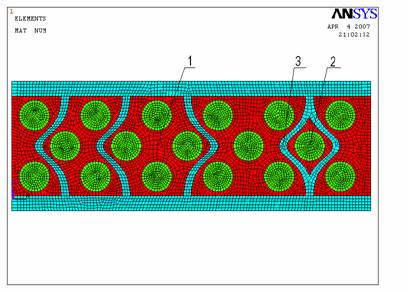
Рисунок 1 – Геометрия слоя

Так как ввиду сложности геометрии задачи ее решение аналитическим методом затруднительно, то целесообразно использовать инженерный пакет ANSYS, который основан на конечноэлементном методе моделирования.

Диффузия влаги определяется дифференциальным уравнением вида:

,

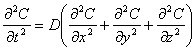где С – концентрация влаги, D – коэффициент диффузии и t – время.

Уравнение, описывающее данный процесс имеет тот же вид, что и уравнение теплопроводности

,

где Т – температура и - коэффициент температуропроводности, который выражается через коэффициент теплопроводности к, удельную теплоёмкость с, и плотность формулой .

Несмотря на то, что уравнения теплопроводности и диффузии похожи друг на друга, метод конечноэлементного моделирования не может быть применён к уравнению диффузии, так как концентрация влаги С в отличие от температуры Т, не является непрерывной функцией при переходе через границы конечных элементов. Однако, для относительной влажности такой проблемы не существует: она удовлетворяет всем необходимым условиям. Для решения задачи теплопроводности с помощью программного комплекса ANSYS необходимо задать коєффициент теплопроводности, удельную теплоёмкость и плотность. Поэтому при решении диффузионной задачи необходимо установить соответствие между этими коэффициентами и коэффициентами, которые входят в уравнение диффузии.

Соответствие между параметрами теплового и диффузионного процессов приведено в таблице 1.

Таблица 1- Соответствие между параметрами теплового и диффузионного процессов

Параметр	Темплопроводность	Диффузия
Переменная	Температура, Т	Относительная влажность,
Плотность		1
Удельная теплопроводность
Удельная теплоёмкость

При конечноэлементном моделировании диффузионной задачи вес влаги, содержащейся в конечном элементе , равен среднему значению концентрации влаги, умноженной на объем элемента

где N – количество узлов элемента и - объём элемента. Относительная влажность в -том узле равна .

Для моделирования процессов сушки и поглощения влаги будем использовать термические конечные элементы, поэтому в соответствии с таблицей 1 используем соответствующие реологические свойства материалов. Для решения уравнения диффузии, которое является дифференциальным уравнением второго порядка, необходимо задать граничные и начальные условия. Если предположить, что в начальный момент времени поверхность имеет относительную влажность равную 100%, то при решении аналогичной “температурной” задачи в качестве граничных условий необходимо ввести Т=1.

Если же происходит высушивание материала, то в качестве граничного условия необходимо ввести Т=0, что соответствует .

Предположим, что исследуемый слой является неоднородным материалом, т.е. однородный материал 1 содержит вкрапления однородного материала 2 (см. рисунок 1). Пусть слой имеет толщину 13мм и состоит из материала 1, при этом он имеет круглые вкрапления диаметром 4мм, состоящие из материала 2. В слое произвольным образом расположены каналы, заполненные воздухом. Сушка рассматриваемого неоднородного слоя вещества происходит как через граничную поверхность, так и через воздушные каналы, пронизывающие слой. Геометрия слоя показана на рисунке 1.

Для моделирования процесса диффузии примем, что физические свойства рассматриваемых материалов такие:

а) первый материал: ,

б) второй материал: ,

в) воздушная среда: ,

Численное решение уравнения диффузии при помощи программного комплекса ANSYS дает ряд интересных результатов:

1) Можно получить изолинии распределения влаги в слое в любой момент времени. Так, например, в момент времени после начала сушки картина изолиний имеет вид (рисунок 2), а изолинии распределения влаги в момент времени представлены на рисунке 3. В оригинале рисунков изолинии относительной влажности представлены цветными полосами. Рядом с рисунками дается легенда для расшифровки числовых значений относительной влажности. Там же приводится ее наибольшее и наименьшее значения.

Рисунок 2 – Распределение изолиний в момент времени

Рисунок 3 – Распределение изолиний в момент времени

2) Полученные результаты дают возможность построить график изменения относительной влажности от времени в любой точке неоднородного слоя.

Например, рассмотрим изменение относительной влажности в точках 1, 2, 3 (рис. 1)

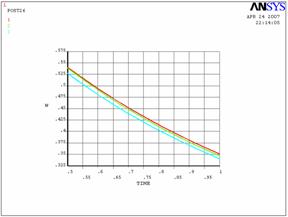
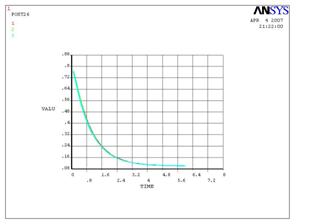
График 1. Изменение влажности в заданных точках с теченинм времени.

Из увеличенного фрагмента графика 1 следует, что на всём промежутке времени вплоть до выхода на плато относительная влажность в точке 1 имеет большее значение чем в точках 2 и 3. В точке 3 наблюдается наименьшее значение влажности, что обусловлено близостью к воздушному каналу.

ЛИТЕРАТУРА

1. Лавриненко Н.М., Сукманов В.А., Афенченко Д.С., Шульга А.В. Конечно – элементное моделирование в расчетах деталей машин. Теория и практика: Учебник – Донецк: ДонГУЭТ, 2006. – 475с.

2. Moaveni S. Finite Element Analysis. Theory and Application with ANSYS. – 2 nd ed. – Pearson Education, Inc. – 2003. – 825p.

3. Buchanan G.R. Finite Element Analysis. - Shaum's outline series, Mc Graw – hill, 1995. - 266p.

4. Madenci E., Guven I. The Finite Element Method and applications in engineering using ANSYS. – Springer Science + Business Media, Inc. – 2006. – 686p.

5. Галлахер Р. Метод конечных элементов. Основы: Пер.с англ. – М.: Мир, 1984. – 428с.