УДК 621.928.24

Коробова О.А., Елемес Д.Е., Вавилов А.В.,. Ликунов А.В.

Восточно-Казахстанский государственный технический университет им. Д. Серикбаева, г. Усть-Каменогорск

О ЗАКОНОМЕРНОСТЯХ СОРТИРОВКИ НЕРУДНЫХ МАТЕРИАЛОВ

НА ПЛОСКИХ ГРОХОТАХ

Процессы сепарации материалов требуют совершенствования из-за их высокой энергоемкости, износа оборудования. Восточно–Казахстанским государственным техническим университетом им. Д. Серикбаева с 1998 года ведутся работы по созданию новых поверхностей грохочения и методов сортировки сыпучих материалов. Одним из направлений этой работы является совершенствования технических моделей процессов грохочения, основанных на описании взаимодействия частиц материала на сите, с учетом его основных геологических характеристик как сыпучей среды.

Поведение отдельной частицы средней округлой формы, и силы действующие на нее, можно проиллюстрировать следующей схемой.

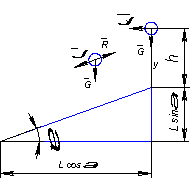
Рис.1 Схема для определения параметров частицы на сите сортирующей машины

Сопротивление передвижению камня от соударения, можно определить как:

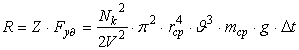; (1)

где F_уд – сила соударения частиц; Z – количество ударов частицы о частицу;

N_k – среднее количество частиц находящихся на сите; V – объем материала, находящегося на сите; r_ср – средний радиус частицы, относительно всего материала, находящегося на сите; скорость движения частицы; m_ср – средняя масса частицы, относительно всего материала, находящегося на сите; g – ускорение свободного падения; Δt – время, необходимое для прохождения частицы.

Векторное уравнение действия сил на частицу массой m представляется как:

(2)

где G – вес частицы.

Далее определеив ускорение (а) т скорость движения частицы можно рассчитать.

Мощность, затрачиваемую на передвижение материала по поверхности сита:

(3)

Таким образом, предложенная методика в первом приближении, дает основные начальные уравнения для более детального описания характера взаимодействия массива сыпучего материала с поверхностью сита.

Для исследования закономерностей грохочения материал рассматривается как многомассовая упруго – вязко – пластичная модель, включающая пять монослоев, что позволяет исследовать движение потока материала, созданная на основе разработок проф. Гончаревича.

Дифференциальные уравнения движения многомассовой упруго – вязко – пластичной модели слоя материала имеют, различный вид в зависимости от взаимного положения монослоев материала [1]. В общем случае возможно 16 различных положений монослоев груза относительно друг друга.

При этом в качестве исходных параметров принимаются следующие:

· С_ij, К_ij – коэффициенты эквивалентные сопротивлению перемещения частицы в направлении осей Y и Х, пропорциональные абсолютной скорости его движения, зависящие от контакта слоев и не зависящие от контакта слоев, соответственно;

· x’, y’ – проекции перемещения частицы на оси неподвижной системы координат:

; (4)

А – амплитуда колебаний короба; ω – частота колебаний короба; m_i – масса материала в i – м монослое:

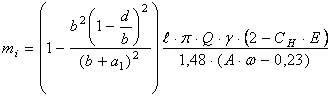; (5)

где b – размер квадратного отверстия, мм; а₁ – толщина проволок сита, мм; d – размер зерна, мм; длина сита, м; Q – секундная производительность, м³/с; γ – плотность сортируемого материала, кг/м³; ω – угловая скорость вращения эксцентрикового вала, м/с²; С_Н – содержание нижнего класса в исходном материале, %; Е – эффективность грохочения, %

Данная работа основана на нахождении оптимального объема, находящегося на поверхности сита, чтобы создавалось максимальное прохождение частиц нижнего класса, а также минимальную засоренность верхнего класса, следовательно, оптимальный расход энергии на процесс грохочения в целом.

Положение № 1 – все монослои в контакте друг с другом и с ситом

В направлении оси у:

(6)

Решение уравнения (6) представляется в следующих видах:

; (7)

Последующие определения дают значения у₂…у₅

Получены основные системы уравнений закона движения монослоев материала в зависимости от их взаимного расположения, их контакта с ситом и между собой, с учетом неравномерного распределения материала по длине сита. Дальнейшая работа сводится к систематизации этих уравнений в единый закон движения материала по поверхности сита, который позволит создать общую теорию грохочения.

Получены виртуальные данные основных параметров работы виброгрохота.

Выявлено, что для достижения максимального грохочения:

- с увеличением частоты колебаний и амплитуды колебаний короба отрыв материала и быстрота перемешивания увеличивается, а также ее прохождения до бункера по ситу снижает количество и массу материала на сите (рисунок 1);

- скорости частиц имеют большее значение при частоте колебаний короба f = 15…25 кол/с (рисунок 2);

- силы сопротивления при увеличении частоты колебаний минимизируются (рисунок 2);

- при изменении угла наклона от α = 2° до 35° получены следующие выводы: при увеличении угла наклона сита от 14° до 35°, концентрация, скорость и мощность имеют более установившейся характер, в отличие от значений при углах от 2° до 12°; выявлена зависимость потребляемой мощности от конструктивно-технологических параметров виброгрохота (рисунок 3).

Рисунок 1 – График изменения Рисунок 2 – График зависимости сил

массы на поверхности сита сопротивления от концентрации на

от частоты колебаний короба поверхности сита

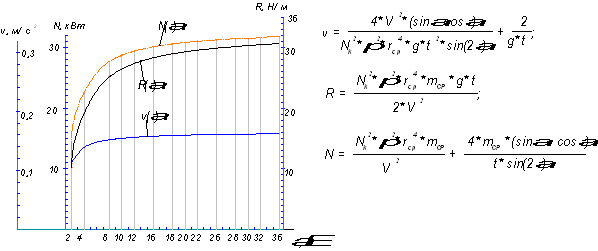
Рисунок 3 – График зависимости сил сопротивления , скорости и мощности от угла наклона поверхности сита

Таким образом, учитывая все выше изложенное можно сделать следующие выводы – в данной работе получены теоретические зависимости, объясняющие связь общих технологических параметров виброгрохота и технологических параметров сыпучего материала, что позволяет в дальнейшем разработать общую концепцию теории грохочения, основываясь на анализе матрицы расположения зерен на поверхности сита.

Список литературы:

1. Кабалкин В.А. Машины для сортировки каменных материалов (грохоты). – Ун-та.: Изд-во Сарат., 1981 г., 96 с.

2. Вайсберг Л.А. Проектирование и расчет вибрационных грохотов. – М.: Недра, 1986 г., 144с.