Турфанов И.Д., Чумаков К.И.,

Запорожский национальный технический университет

Лютый А.П.

ОАО электрометаллургический завод “Днепроспецсталь” им. А.Н. Кузьмина

Гармонический синтез законов регулирования координат

электротехнологического комплекса мощной дуговой

сталеплавильной печи.

Введение

Важнейшей задачей энергетического комплекса Украины на современном этапе развития рыночной экономики является задача устойчивого динамического энергоэффективного функционирования электротехнологической отрасли. Современное состояние электроэнергетики (как и экономики в целом) Украины в условиях энергодефицитности оценивается как находящееся в переходном неустойчивом периоде развития.

Основным фактором, вызывающим трудности в поддержании устойчивого экономико-эффективного энергообеспечения промышленного и агропромышленного комплекса является природная энергодефицитность, низкая энергоэффективность ее использования, особенно в горнометаллургическом комплексе. Особенно актуальны эти факторы для электросталеплавления приднепровского и запорожского региона. Ниже рассматриваются вопросы электротехнического обеспечения повышения энергоэффективности электросталеплавения на базе дуговых сталеплавильных печей ёмкостью 50-200 тонн.

Задачи исследований и обсуждение их результатов

Мощные дуговые сталеплавильные печи имеют электротехнический комплекс, параметры которого зависят от параметров (Zi) системы электроснабжения, печного трансформатора (ПТ), “короткой сети”, расплава ванны и др. (рис 1.) [4,5]:

Рис. 1 Параметры импеданса дуговой печи: – кабеля питания ПТ, - стороны ВН ПТ, - стороны НН ПТ, - неподвижных “башмаков”, - гибкого кабеля, - подвижных “башмаков”, - трубошины, - электрододержатели электрода (на одну фазу), - расплава ванны.

Основными нелинейными элементами являются , , . Математическое описание такой системы требует методологии аналитического представления нелинейных характеристик, устанавливающих связь между электрическими и магнитными величнами: а) в линейной постановке: ; ; ; б) в нелинейной постановке они представляются в виде функциональных связей: ;;.

Аналитическое описание нелинейной цепи ПТ предполагают, что характеристика нелинейного элемента в ее определенной области приблизительно совпадает с видом математической функции в виде конечного математического выражения как результата интегрирования дифференциальных уравнений соответствующего нелинейного импеданса. В данном случае аппроксимация характеристик заключается в выборе типа аппроксимирующей функции и определения ее коэффициентов: а) степенного полинома: , б) экспоненциального полинома: , в) тригонометрический полином:

г) трансцендентными функциональными полиномами [1,2] и др. общим методом таких подходов является метод гармонического анализа [1], который применим и к описанию механического импеданса системы регулирования мощности печи [2,4,5]. В данном случае проводится: а) определение зависимости между заданной и искомой величиной, б) задание закона изменения (временной зависимости) воздействующей величины, в) закона изменения (временной зависимости) искомой величины, г) гармонический анализ искомой величины, д) оценка искажения. В этом случае коэффициенты вычисляются по соотношениям [3]: ; ; ; где - среднее значение 2m ординат, - удвоенное среднее арифметическое значение произведений значений в точках 2m на соответствующее значение ; - удвоенное среднее значение произведения значений функции в точках m на соответствующее значение .

1) зависимость степенного полинома и разложение с помощью перехода к тригонометрической функции кратного аргумента. Пусть ВАХ нелинейного элемента (НЭ) представлена степенным полиномом вида: ; - ток, U – синусоидальная функция времени . В этом случае упрощается определение коэффициентов гармонического анализа при переходе от тригонометрической степенной функции к тригонометрической функции кратного аргумента при использовании известных тригонометрических зависимостей:

(1)

В общем случае

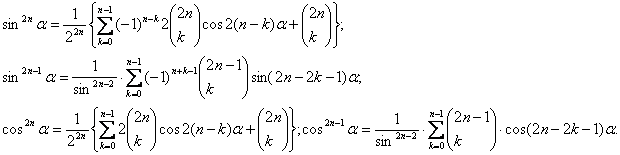
При учете нелинейности конденсаторов БСК величина тока, в первом приближении, представляется полиномом третьего порядка вида

. При , тогда или с учетом соответствующих значений (1) имеем: . Постоянная составляющая , амплитуда третьей гармоники .

2) Тригонометрический полином и разложение на отдельные гармоники, амплитуды которых являются функциями Бесселя [5] от действительного аргумента. Если при аппроксимировании используется тригонометрический полином и заданная входная величина изменяется по гармоническому закону, то выходная величина будет иметь вид (в обобщенной форме):

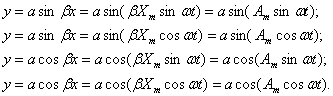(2)

Тригонометрические функции выражаются степенными рядами вида

Тогда по (2) для 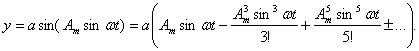При замене по (1) степень тригонометрической функции через тригонометрическую функцию с кратким аргументом, получаем:

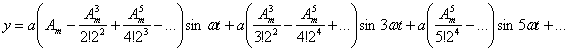(3)

Функции Бесселя также выражаются рядами. Для функции n-го порядка общее выражение имеет вид [1]:

(4)

При сравнении (3) и (4) имеем:

, т.е. ряд состоит из нечетных гармоник, амплитуды которых . Аналогично имеем:

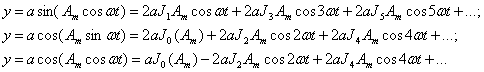
3) Экспоненциальная функция и разложение на отдельные гармоники, амплитуды которых являются функциями Басселя от мнимого аргумента. В этом случае [5] для аппроксимации применяется экспоненциальная функция и для гармонической входной величины выходная величина будет иметь вид:

(5)

(6)

функция и (5) принимает вид: или, при выражении степени тригонометрической функции с помощью функций Бесселя от мнимого аргумента :

окончательно имеем:

.

По аналогичным для (6) получим:

. (7)

4) Трансцендентные функции с синусоидально изменяющимся аргументом и их разложение.

В случае использования гиперболического синуса гармонический анализ приводится по выражению , т.е. после выражения гиперболического синуса рядом , будем иметь .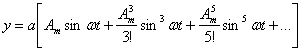

При замене тригонометрической функции тригонометрической функцией от кратного аргумента (1) получаем:

.

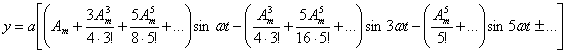Выражение в скобках представляют собой амплитуды соответствующих гармоник, т.е. после сравнения по (6) и (3) следует, что их амплитуды гармоник представляют собой функции Бесселя от мнимого аргумента вида .

При использовании получаем и при разложении для величины будем иметь .

5) Аппроксимация тригонометрическим полиномам функции, аргумент которой содержит синусоидальную постоянную составляющие: .

Если используется экспоненциальный полином, то функция

. Если функция аппроксимируется тригонометрическим полиномом, то ее выражение:

В случае аппроксимации гиперболическим синусам функция у равна:

6) Метод нескольких ординат.

В случае анализа системы с нелинейной индуктивностью и влияния взаимоиндуктивности, характеристика , которая управляется синусоидальным напряжением , то можно эту характеристику аппроксимировать степенным полиномом и определить составляющую высших гармоник.

В первом приближении может быть применен метод 3 ординат [6]. Если имеется характеристика с постоянным прогибом вниз, то ее можно в требуемой области аппроксимировать квадратичной зависимостью. Пусть границы области управления в заданных приделах (+1,-1): ; . В этом случае коэффициенты определяются координатами принятых к рассмотрению точек характеристики , откуда следует . При использовании в качестве источника питания мощный тиристорный преобразователь, управляющая величина имеет косинусоидальную форму , откуда . В данном случае амплитуды отдельных гармоник составляют:

Для случая аргумента с постоянной и синусоидальной составляющими амплитуда основной гармоники будет иметь вид: .

Принимается: - максимальное значение при , т.е. откуда амплитуда основой гармоники .

7) Точность метода нескольких ординат. Управляемая характеристика НЭ аппроксимируется степенным полиномом 2,4 и т.д. степени. Ограничение степени и полинома вызывает ошибки, т.к. абсолютную точность представляется возможным получить при аппроксимации полиномам, когда n стремится к бесконечности, т.е. . Если X – нормированная величина, . При разложении в ряд Фурье правая часть содержит только косинусные составляющие, т.е.

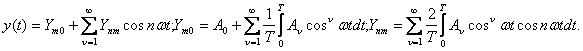
Величины представляют собой точные значения коэффициентов соответствующих гармоник. Оценка интегралов и проводится с учетом того, что:

и т.д.

Применяя для методы 3 и 5 координат, можно получить приближенное значение для .

При заданных значениях

Метод трех координат дает приближенное значение амплитуд соответствующих гармоник:

Абсолютная ошибка для метода трех координат составит:

.

Аналогично ошибки для метода пяти ординат составят:

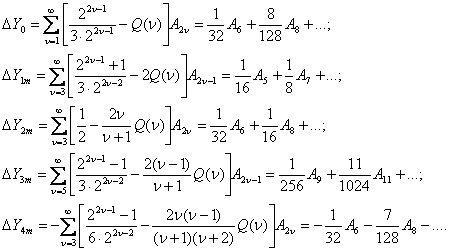
Анализ прорведенных исследований качества аппроксимации (ошибок) показывает, что при методе трех ординат члены с или методе пяти ординат не оказывают влияние на величину ошибки, т.е. на высокочастотные составляющие ошибки, что упрощает анализ.

Заключение

Полученные результаты являются эффективным инструментом аналитического конструирования регуляторов для стохастических процессов преобразования энергопотоков в технологическую теплоту плавления, в мощность в дуговых сталеплавильных печах на базе итерационного варьирования коэффициентов объекта и регулятора. В таком одновременном решении задач оптимального управления и стабилизации для нелинейных объектов расширяются алгоритмические возможности структурного подхода к решению задач, наблюдаемости основных типов структур электросталеплавильных агрегатов при плавлении металлов по технологии высшего уровня. В данном случае при определенных предпосылках конструкторски - технологического характера и структурных приближениях приводится нелинейное дифференциальное уравнение к параметрическому, при этом обратная постановка задачи не представляет фактического интереса, так как технические задачи почти всегда описываются нелинейными, а не параметрическими дифференциальными уравнениями.

Литература

1. Справочник по теории автоматического управления / Под ред. Ф.Ф.Красовского.- М.: Наука,1987.-712с.

2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики.- СПб.: Лань,1998.- 736с.

3. Камке Э. Справочник по обыкновенным дифференциальным уравнениям.- М.: Наука,1965.- 704с.

4. Короткие сети и электрические параметры дуговых электропечей: Справочник/ Я.Б.Данцис, Л.С.Кацевич,Г.М.Жилов и др.; Под ред.Я.Б.Данциса, Г.М.Жилова.- М.: Металлургия, 1987.- 320с.

5. Труфанов И.Д. Системы оптимизации режимов работы мощных дуговых сталеплавильных печей на основе интегрального критерия энергосбережения / Дисс…. докт.техн.наук.- Запорожье, 2001.- 530с.

6. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике.- М.: Наука.1980.- 688с.