ТЕМПЕРАТУРНЫЙ ЭФФЕКТ СМЕШЕНИЯ ГАЗОВ

УДК 533.27

Температурный эффект смешения газов

Павлов А. М, Троеглазова Т. В.

Восточно-Казахстанский государственный университет имени С. Аманжолова, г. Усть- Каменногорск .Казахстан (070010 Севастопольская 7/1,30) ampavlov@mail.ru

Выведена и проанализирована формула для расчета температурного эффекта смешения газов. Расчетная формула проверена в результате теоретического расчета на примере смесей газов: , , . Полученное уравнение позволило удовлетворительно описать экспериментальные данные по температурному эффекту смешения газов.

Ключевые слова: температурный эффект, комплексы молекул, кластер, концентрация.

Introduce and analyze the formula for calculating the temperature effect of gas mixing. The calculation formula is tested by a theoretical calculation on the example of mixtures of gases: The resulting equation is allowed to satisfactorily describe experimental data on the thermal effect of mixing gases.

Key words: temperature effect, complex molecules, clusters, concentration.

Когда говорят о температурном эффекте смешения газов, то имеют ввиду изменение температуры смеси при . Этот эффект практически не упоминается в публикациях. Нам известна лишь одна работа И. Г. Шамсутдинова, который пытался экспериментально изучить этот эффект. В [1] лишь упоминается об измерении температурного изохорно-адиабатического эффекта смешения системы аргон-двуокись углерода при температуре и различных давлениях. Никаких числовых значений не приведено. Сказано лишь, что эффект может достигать 11%. Далее автор говорит о большой погрешности опытов (около 10%) и необходимости дальнейших исследований.

В книге Павлова А. М. «Комплексы молекул и их влияние на свойства газов»[2] выведены для них формулы, но сравнение с экспериментальными данными проводилось недостаточно.

В данной статье восполняется этот пробел.

Сложность опытов по измерению при смешивании газов вполне понятна. С одной стороны газы должны быть смешаны очень быстро, чтобы температура не успела измениться вследствие теплопроводности стенок. С другой стороны для полного перемешивания газов нужно время. Видимо по этой причине, не считая свои данные убедительными, автор их не приводит [2].

Попробуем осветить это явление теоретически. Первый газ из объема , расширяется до объема , а второй газ от объема , до . Получается, что каждый газ совершает работу по расширению до соответствующего объема. Кроме этого, как выше было показано, меняется концентрация комплексов молекул, комплексы распадаются за счет кинетической энергии молекул. Эти две причины и должны приводить к понижению температуры смеси.

В случае адиабатического расширения газа сохраняется энтальпия. Следовательно

или

, (1)

где - давление смеси сразу после смешивания при температуре Т. Отсюда видно, что для определения необходимо записать внутреннюю энергию газов до и после смешивания. Кроме этого, следует определить , которое не равно барическому эффекту смешения, так как температура не равна .

Как было показано выше, внутренняя энергия газа, если , равна:

, (2)

где .

Чтобы записать внутреннюю энергию смеси, необходимо пользоваться выражением для F смеси. Поскольку второй вириальный коэффициент чистого газа равен В мономера, в должны стоять В мономеров и концентрации компонентов, а не кластеров. Далее вместо будет , где буквами «А» и «В» будем обозначать компоненты. Таким образом,

, (3)

где .

Запишем внутреннюю энергию аргона и углекислого газа, а так же их смеси; поскольку у этой смеси есть хоть какие-то экспериментальные данные по температурному эффекту смешения [1].

У аргона критическая температура 150К, а у углекислого газа 304К. Таким образом, при аргон находится при температуре выше критической, степень его кластеризации мала и для , следует воспользоваться следующей формулой:

. (4)

Углекислый газ при становится насыщенным паром при , то есть . В [1] опыты по барическому эффекту проводились при давлениях от 1 до . Тем не менее, для СО₂ будем брать внутреннюю энергию в виде, написанном выше, пренебрегая х₂, поскольку он всё таки далек от критического состояния.

У однородных молекул наблюдается резонансное взаимодействие, вследствие которого энергия притяжения становится на порядок выше энергии обычного вандерваальсова взаимодействия. В связи с этим, будем учитывать лишь комплексы из однородных молекул. В этом приближении внутреннюю энергию смеси можно записать в следующем виде:

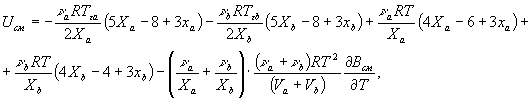(5)

где , а и - глубина потенциальной ямы в потенциале Леннарда – Джонса и она отрицательная.

Выше говорилось, что для нахождения необходимо найти разность

Подставим сюда :

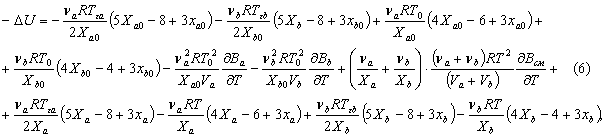
В этой формуле Х_а и Х_b относятся к температуре Т, которая будет в смеси сразу после смешения газов, Х_а0 и Х_b0 относятся к начальной температуре Т₀.

В работе [2] показано, что

. (7)

Эти равенства были получены в случае смешивания газов при постоянной температуре, то есть при Т=Т₀. Вообще говоря, поскольку и при том же объеме. Однако, учитывая малость изменения температуры, можно пренебречь изменением вследствие наличия . В самом деле, так как

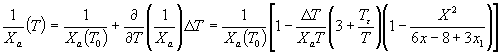то слагаемым, содержащим можно пренебречь по сравнению с единицей. Поэтому будем считать и , то есть предполагается, что концентрация комплексов меняется лишь вследствие расширения газа.

Заменим Т через и через , через используя (7):

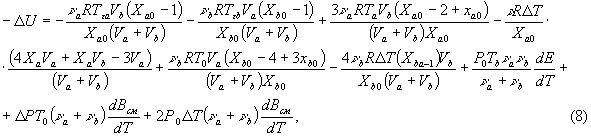
где .

Выше было записано, что . Преобразуем далее . Так как при барическом эффекте смешения давление замерялось, то можно привести давление смеси при температуре Т к давлению Р при температуре :

Тогда, получим:

. (9)

Приравнивая это выражение к и вводя вместо , получим формулу для . Необходимо еще отметить, что если Х искать по PVT – данным, то в уравнении состояния можно считать, что круглая скобка входит в Х и записать его в виде .

После не сложных преобразований получим:

где . (10)

При получении этого выражения слагаемые, содержащие вириальные коэффициенты, не учитывались.

Определив по РVТ данным и , а так же и , подставим в полученное нами выражение и учтем, что в опытах [1] было и . Тогда получим: , что находится в удовлетворительном согласии с опытом. И. Г Шамсутдинов приводит лишь максимальное изменение температуры в 11%, не указывая давления при котором оно получено. Возможно, что учет , где и даст лучшие результаты.

Сравнить с экспериментом невозможно, поскольку опытных данных по температурному эффекту смешения просто нет. Давление в 5,5МПа при Т=293К является для областью насыщенного пара и жидкости. Поэтому в этой точке плотность в справочнике Н.Б. Варгафтика отсутствует.

Данные таблицы 5 из [1] показывают, что максимальный барический эффект смешения будет при . Хотя в нашей формуле и входят не совсем симметрично, следует ожидать, что и температурный эффект будет максимален при этой же объемной концентрации. Ниже в таблице 1 приведены значения , подсчитанные по полученной формуле.

Таблица 1 – Значения температурного эффекта смешения некоторых газов



270	1	0,0080905	-0,00781	0,074037	-0,00275	0,0197	-0,0056
	2	0,017382	-0,01643	0,020635	-0,01798	0,0436	-0,01906
	3	0,039068	-0,0511			0,0815	-0,0576
290	1	0,006231	-0,00563	0,004704	-0,00173	0,017	-0,00625
	2	0,009583	-0,00365	0,012298	-0,00969	0,037	-0,017
	3	0,0206622	-0,01978			0,0607	-0,03484
	4	0,040143	-0,04749	0,03998	-0,04482	0,0896	-0,05984
300	1	0,005309	-0,00494			0,015	-0,00646
	2	0,011527	-0,01154	0,011421	-0,01047	0,0321	-0,01475
	3	0,018606	-0,01958
	4	0,027302	-0,02957	0,027208	-0,0269	0,071	-0,039
	5	0,039686	-0,04601
	6	0,062572	-0,07536	0,063263	-0,07009	0,136	-0,099