География и геология / 5.Картография и геоинформатика

К.т.н., доцент, Кузнецова И.А., , магистрант, Тюлегенова А.В.

Казахский национальный технический университет имени К.И. Сатпаева

Исследование точности фотограмметрической обработки стереопар космических сканерных снимков, полученных со спутника GeoEye.

Развитие средств дистанционного зондирования Земли, технологий спутникового позиционирования, методов и алгоритмов обработки данных на основе совершенствования вычислительной техники способствовали развитию геоинформационных технологий. Одним из обязательных слоев геоинформационных приложений является слой цифровой модели рельефа (ЦМР). Кроме обычного использования ЦМР в картографии, можно привести следующие области, где использование геоинформационных технологий и ЦМР позволили получить новые интересные результаты - геологии, геоморфологии, мониторинг современного вулканизма, системы гидрологического назначения, градостроительная деятельность, землеустройство нефтепромыслов и т.д. Цифровые модели рельефа могут использоваться либо самостоятельно, либо как высотная основа для ортотрансформирования изображений местности и создания картографической продукции. Для получения ЦМР на большие территории наиболее эффективным решением является применение космических снимков с последующей обработкой на цифровых фотограмметрических станциях.

Для исследования точности фотограмметрической обработки была использована стереопара космических изображений на территорию города Хобарт (о. Тасмания, Австралия), полученная 17 февраля 2009 года со спутника GeoEye-1. Работы проводились на цифровой фотограмметрической станции PHOTOMOD.

Стереопара космических снимков была получена в результате синтеза исходных пар снимков с панхроматическим разрешением 0,5м и мультиспектральным разрешением 2,0м в программе PHOTOMOD версии 4.4.

Для осуществления измерения сети был использован модуль PHOTOMOD AT, позволяющий выполнять работу в несколько этапов. На первоначальном этапе был загружен каталог координат опорных точек путем импорта текстового файла, который был представлен поставщиком услуг. На следующем этапе было произведено измерение опорных точек стереопары. На рисунке 1 показана возможность опознавания опорных точек и объектов местности с достаточно высокой точностью, благодаря отличной геометрии и пространственному разрешению космических снимков.

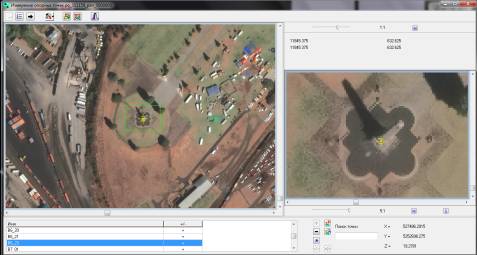
Рисунок 1. Измерение опорных точек.

Перенос опорных точек на соседнее изображение выполнялось ручным позиционированием, без использования коррелятора. Всего было измерено 15 опорных точек из имеющегося каталога. Максимальный параллакс при идентификации соответствующих точек на правом изображении составил 0.394, а СКО – 0.248 (значения приведены в пикселях).

Для перехода на этап уравнивания был запущен PHOTOMOD Solver. На рисунке 2 показана геометрия расположения точек на снимках. Точки на изображениях расположены неравномерно, что связано с рельефом местности. В северо-западной части точек меньше всего, это объясняется большими высотами рельефа.

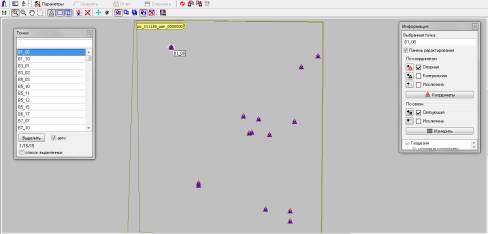
Рисунок 2. Схема уравнивания

Так как стереопара содержит RPC коэффициенты, предоставленные поставщиком данных, то при уравнивании проекта автоматически применяется алгоритм, учитывающий эти коэффициенты,

Для оценки качества исходной модели космических снимков и суммарной точности опознавания и измерения опорных точек всем опорным точкам был задан статус – контрольные. Это позволило оценить точность согласования опорных точек между собой и позволило оценить, с какой ошибкой возможно определение положения точки на местности, используя только исходные RPC коэффициенты. Отчет об уравнивании представлен в таблице 1.

Таблица 1. Оценка качества исходной модели и точности положения точки на местности.

Наименование ошибок	dX	dY	dZ
	Контрольные точки
Среднеквадратическая	2.691	0.647	9.356
Средняя	2.581	0.600	8.981
Максимальная	3.189	0.939	11.460

Из таблицы 1, видно, что согласованность опорных точек высокая, о чем говорят малые различия среднеквадратических, средних и максимальных ошибок. Ожидаемая точность внешнего ориентирования может быть равной 0,5м. в плане и 1,5м. по высоте, что следует из разностей средних и максимальных ошибок. Также по результатам, приведенным в таблице 1, можно предположить наличие систематических ошибок. Это видно исходя из близости значений всех видов ошибок, приведенных в указанной таблице.

Для дальнейшей оценки качества внешнего ориентирования одной из точек было присвоено значение опорной, а у всех остальных остался статус контрольных. В таблице 2 приведены результаты оценки качества внешнего ориентирования.

Таблица 2. Оценка качества внешнего ориентирования по одной опорной точке

Наименование ошибок		dX	dY		dZ
		Контрольные точки
Среднеквадратическая		0.537	0.352		1.177
Средняя		0.483	0.299		1.015
Максимальная		0.778	0.578		2.182
	Опорная точка
Среднеквадратическая	0			0		0.001
Средняя	0			0		0
Максимальная	0			0		0.001

Результаты уравнивания показали, что использование всего одной опорной точки, взятой произвольно, приводит к резкому снижению влияния систематических ошибок на точность внешнего ориентирования.

При использовании двух опорных точек наблюдается влияние систематических ошибок на расхождение координат на опорных точках. Но что касается контрольных точек, то их точность ориентирования повышается, но уже не так значительно по сравнению с использованием одной опорной точки. Результаты приведены в таблице 3.

Таблица 3. Оценка качества внешнего ориентирования по двум точкам

Наименование ошибок		dX	dY		dZ
		Контрольные точки
Среднеквадратическая		0.274	0.232		0.956
Средняя		0.193	0.162		0.783
Максимальная		0.579	0.468		1.915
	Опорная точка
Среднеквадратическая	0.073			0.228		0.590
Средняя	0.073			0.228		0.589
Максимальная	0.077			0.237		0.594

Несмотря на общее повышение качества внешнего ориентирования, использование двух опорных точек при уравнивании не позволяет получить допустимую точность для дальнейшей обработки проекта.

В связи с этим в проекте пяти точкам из пятнадцати был задан статус опорных. Результаты уравнивания приведены в таблице 4.

Таблица 4. Оценка качества внешнего ориентирования по пяти точкам

Наименование ошибок		dX	dY		dZ
		Контрольные точки
Среднеквадратическая		0.199	0.156		0.248
Средняя		0.186	0.127		0.202
Максимальная		0.296	0.299		0.441
	Опорная точка
Среднеквадратическая	0.097			0.114		0.328
Средняя	0.078			0.089		0.307
Максимальная	0.165			0.218		0.459

Для получения окончательного результата уже десяти точкам из пятнадцати было присвоено значение опорных. Краткое содержание отчета об уравнивании приведено в таблице 5.

Таблица 5. Оценка точности внешнего ориентирования по десяти опорным точкам

Наименование ошибок		dX	dY		dZ
		Контрольные точки
Среднеквадратическая		0.208	0.237		0.509
Средняя		0.195	0.209		0.436
Максимальная		0.296	0.360		0.796
	Опорная точка
Среднеквадратическая	0.147			0.102		0.173
Средняя	0.120			0.079		0.124
Максимальная	0.288			0.230		0.412

Точность окончательного результата зависит от точности опознавания опорных точек на изображениях, а так же точности самих координат опорных точек. Из приведенных выше таблиц совершенно очевидно, что при использовании всего лишь одной опорной точки, результаты оценки точности внешнего ориентирования значительно повышаются. Отсюда следует, что чем большее количество точек будет использовано как опорные, тем лучшие результаты нам удастся получить. Но опытным путем было установлено, что наиболее оптимальные результаты были получены при использовании всего лишь пяти опорных точек. Следовательно, при фотограмметрической обработке космических снимков для получения удовлетворительных результатов достаточно иметь координаты пяти точек, полученных полевой геодезической привязкой. Это позволяет намного уменьшить трудоемкость работ связанных с картографированием малообжитых, труднопроходимых районов и повысить оперативность получения выходных данных.

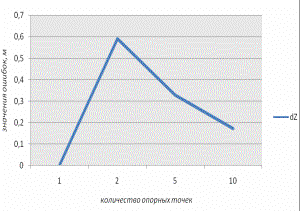
По результатам уравнивания были построены графики зависимости, которые показаны на рисунке 3. На графиках наглядно прослеживается динамика изменения значений ошибок с увеличением количества опорных точек.

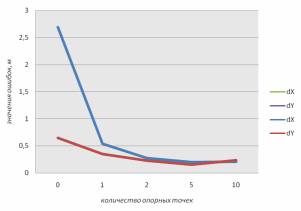
а) б)

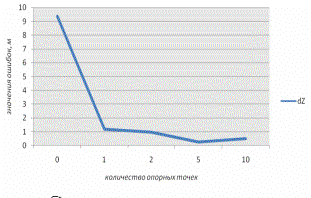
в) г)

Рисунок 3. Графики зависимости значений расхождений от количества опорных точек: а) расхождения на контрольных точках в плане, б) расхождения на опорных точках в плане, в) расхождения на контрольных точках по высоте, г) расхождения на опорных точках по высоте.

Наилучшие результаты уравнивания позволили приступить к следующему этапу обработки сети в модуле PHOTOMOD DTM, который заключался в построении цифровой модели рельефа.

Литература:

1. Назаров А.С. Фотограмметрия. – Минск, НТООО «ТетраСистемс», 2010. 398с.

2. Руководство пользователя по программе PHOTOMOD версии 4.4.

3. Зубарев А.Э. Обработка стереопары космических изображений. – Москва, «Ракурс».