ОРТАЛЫҚ ТАРТЫЛЫС ӨРІСІНДЕГІ ҚОЗҒАЛЫС

 

Сырым Ж.С.–  п.ғ.к., М.Өтемісов атындағы Батыс Қазақстан мемлекеттік универвитетінің «Физика және математика» кафедрасының доценті,

Қажмуханова Г.Ш.– магистрант

 

Есептің қойылуы.

Орталық тартылыс өрісіндегі дененің қозғалысы жөніндегі есеп физикалық заңдарға бағынатын нысанның тәртібін зерттеу үшін дербес компьютерді пайдаланып демонстрациялаудың жақсы мысалы.

Жасанды серікті орбитаға шығару үдерісі екі деңгейден тұрады. Бірінші деңгейде Жердің жасанды серігі атмосферада белгілі бір биіктікке вертикаль көтеріледі. Содан кейін зымыран тасымалдаушының соңғы басқышы оған қажет горизонталь жылдамдық береді де ол ары қарай инерция бойынша қозғалады.

Кішкене дененің (жасанды серіктің) үлкен массалы денемен (Жермен) тартылу центрі маңындағы инерциялық ұшуын қарастыралық: жасанды серіктің траекториялары қандай болуы мүмкін, Жерге құламай дөңгелек траекториямын қозғалуы үшін (бірінші ғарыштық жылдамдық) Жер бетіне жақын жерде оның ең минимал жылдамдығы қандай болуы керек, тұйық емес траекторияға шығуы үшін және Жерден ұшып кетуі үшін (екінші ғарыштық жылдамдық) жасанды серіктің минималь бастапқы жылдамдығы қандай болуы керек. Сандық экспериментте сонымен қатар Кеплер заңдарын да тексеруге болады: тартылу центрі орбитаның бір фокусында орналасқан; Күннен планетаға дейінгі радиус вектор бірдей уақыт аралығында бірдей аудандар «сызады»; жасанды серіктердің тартылыс центріндегі айналу периодтарының квадратының қатынасы олардың орбиталарының эллипстерінің үлкен жарты өстерінің кубтарының қатынасына тең болады.

Модель негізінде бүкіләлемдік тартылыс заңын аламыз. Қозғалысы қарастырылатын денеге тек тартылыс күші әсер етсін. Сонда Ньютонның екінші заңының теңдеуі мына түрде жазылады:

,                                                                                        (1)

мұндағы m және М – жасанды серіктің және тартылыс центрінің массалары, G - гравитациялық тұрақты,  r - тартылыс центріне қатысты жасанды серіктің орнын анықтайтын радиус-вектор, а – жасанды серіктің үдеуі. (1) түріндегі бүкіләлемдік тартылыс заңы материялық нүктелер үшін жазылған, оның сфералық-симметриялық денелер үшін де түрі осындай болады.

Орталық күш әсерінен болатын денелер қозғалысы бір жазықтықта жүзеге асады, оның орны дененің бастапқы орны  және оның   бастапқы жылдамдық векторларымен анықталады. Декартттық координаттар жүйесін тартылыс центріндегі басымен және уақыттың санақ басын қозғалыс x , y жазықтығында болатындай және бастапқы мезетте дененің жылдамдығы x өсіне перпендикуляр болатындай етіп таңдап аламыз (1-сурет).

 

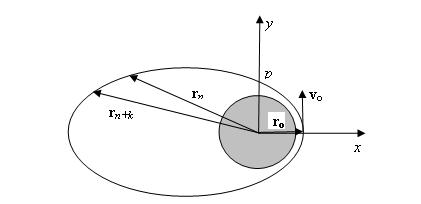
1-сурет. Координаттар жүйесі және жасанды серіктің мүмкін траекториясы.

 

Онда бастапқы шарттарды мына түрде жазуға болады:

.                                                                (2)

Сөйтіп (1) теңдеуі (2) шартымен толығымен жасанды серіктің траекториясын және оның барлық қасиеттерін анықтайды.

Сандық модель.

Есептің сандық талдауын өлшем бірліктер негізінде есептің сипатттық масштабтарды қолдана отырып жүргізген ыңғайлы. Ұзындық бірлігі ретінде х-ті алу қолайлы. Ал Жердің жасанды серігі үшін бұл шама Жердің R  радиусының реті және ол (R + h)-қа тең болады, мұндағы h  –жасанды серіктің Жер бетінен биіктігі. Енді барлық қашықтық оған қанша x0  сәйкес келетіндікпен анықталады. Өлшемсіз х метрмен өлшенетін х0-ге бөлінген метрмен өлшенген х-ке тең болады. Уақыт бірлігін гравитациялық тұрақтыны және тартылыс центрінің сипаттамаларын қолданып тұрғызған ыңғайлы. Сонда (1) теңдеуден  көбейткішінің үдеудің өлшемділігі (м/с2) болатындығын көру оңай  R қашықтықтың орнына x0-ді алып, өрнекті уақыт өлшемділігімен (с) сәйкестендіреміз: . Осыны уақыт бірлігі ретінде аламыз. Жылдамдық бірлігі ретінде , яғни -ді аламыз.

Осы бірліктерде өлшенген үдеудің құраушылары төмендегі теңдеулермен анықталады (осында және ары қарай өлшемсіз физикалық шама үшін өлшемді шамаларға сәйкес қолданылатын белгілеулер қолданылады):

 ,                                                  (3)

Ал бастапқы шарттар мына түрде жазылады:

           ,                                                             (4)

мұндағы .

Енді барлық физикалық шамалар салыстырмалы бірліктер арқылы өлшенеді және «жасанды серік-тартылыс центр» барлық жүйесі үшін бірдей болады. Есептегі параметрлердің саны азайды. Жалғыз өлшемсіз параметр V0, ол есепте бастапқы мезетте жасанды серіктің кинетикалық және потенциалдық энергияларының арасындағы қатынасты көрсетеді. Шындығында, жасанды серіктің кинетикалық энергиясы бастапқы уақыт мезетінде , потенциалдық энергия тартылыстың ньютондық заңы үшін , және  .

Әртүрлі уақыт мезетіндегі жасанды серіктің жылдамдық құраушыларын және оның координаттарын табу үшін уақыттық өске tn дискретті нүктелерді таңдап аламыз, олар бір-бірінен Δt аз интервалға қалып отырады. Онда tn+1 уақыт мезетіндегі және  жылдамдық құраушылары шамамен былай өрнектеледі (уақыттың бұл интервалында үдеуді өзгермейді деп есептейміз):

,                                                                                (5)

,                                                                                (6)

ал осы мезеттергі координаттарды бірқалыпты қозғалыс үшін есептейміз (тағы да Δt аз уақыт интервалында жылдамдық көп өзгермейді деп аламыз):

,                                                                               (7)

.                                                                              (8)

Бастапқы уақыт мезетінде жасанды серіктің жылдамдық құраушылары мен координаталары белгілі:

.

Сонда (5)-(8) теңдіктер жүйесі Dt аз қадаммен жасанды серіктің траекториясын және оның барлық сипаттамаларын дәл есептеуге мүмкіндік береді.

Траекторияны классификациялау үшін олардың е эксцентриситетін есептеу ыңғайлы. Эксцентриситетті есептеу үшн таңдалған координат жүйесінде  үшін траекториядағы нүктенің  координатын анықтау қажет. Онда . Егер , онда траектория тұйық қисық болып табылады ( кезінде шеңбер,  кезінде эллипс),   кезінде (сандық экспериментте бұл мән дәл шықпауы мүмкін), траектория парабола, ал  кезінде траектория гипербола болып табылады.

Кейбір  уақыт кезінде радиус вектор сызатын ауданды былай есептеуге болады:

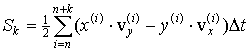.                                                         (9)

Траекторияның әртүрлі бөліктерінде есептелген бұл аудандарды салыстыру қызық. Олар Кеплердің екінші заңы бойынша тең болу қажет.

Кеплердің үшінші заңы бойынша айналу периодтарының квадратының қатынасы орбиталардың үлкен жарты өстерінің кубының қатынасына тең, яғни әрбір траектория үшін К3 = Т 2/а3 шамасы тұрақты болып қалу қажет. Эллипстің үлкен жарты өсінің ұзындығын табу үшін y = 0 кезінде xмин теріс координатты табу қажет. Сонда tм уақыт мезеті болған кезде бұл жасанды серіктің айналу периодының жартысына сәйкес келу қажет. Сонымен, үлкен жарты өстің шамасы мынаған тең: , ал периоды T = 2tм.

Delphi тілінде есепті модельдеу.

Бірінші есепте виртуаль зертханалық ортада жұмысты түсінікті етіп көрсетеміз. Бұл ортаның мүмкін түрі 2-суретте келтірілген. Басқарудың көп бөлігі негізгі терезеде көрсетілгендіктен, оның қарастырылуына басты назар аударалық. Келтірілген суретте негізгі терезе түсінікті деп ойлаймыз.

Қарастырылатын терезенің сол жақ бөлігінде  төрт енгізу өрісі бар панель орналасқан, онымен графикалық терезелерді басқаруға болады. Сұлбалы тіктөртбұрыышты графикалық экранның жанында X және  Y өстерінің максималь және минималь мәндерін енгізуге болатын жолдар бар. Негізгі терезеге енгізілетін барлық параметрлер сияқты координаталарды «физикалық» бірліктер жүйесінде жазу керек.

Келесі панель негізгі терезенің центрінде орналасқан, ол есептің берілгендерін жасанды серіктің V0 жылдамдығын және dt (Dt-есептің берілгенінде) уақыт қадамын енгізуге және де есептеулерді жүргізуге және тоқтатуға арналған. Сонда V0-дің мәнін беру екі тәсілмен жүргізіледі. Бірінші жағдайда график параметрдің бір мәні үшін тұрғызылады: ол «Один график для» жазылған өрісте беріліп, бағдарлама «Счет-1» батырмасын басудан кейін жүргізіледі. Екіншісінде, бірнеше траекторияны бірден автоматты түрде есептеу жүргізіледі. Сөйтіп V0-дің бастапқы және соңғы мәндері енгізіледі, ол қажет есептеулерді жүргізу үшін қажет, тізімнен қажет траекторияның саны (олар 2-ден 11-ге дейін болуы мүмкін) таңдалып, «Счет-М» батырмасы басылады. Есептеулерді жүргізудің екі көрсетілген режимдерін сәйкес келуі сандық эксперименттерді өткізуге ыңғайлы болып табылады. Екі жағдайда да кез келген мезетте «Стоп» батырмасын басу арқылы есептеулерді тоқтатуға болады.

 

2-сурет. Виртуаль зертханалық ортаның мүмкін түрі.

Негізгі терезенің оң жағында басқарудың үш пайдалы органы бар: траекторияларды салудың түстерін таңдау және екі батырма графикалық терезені және кестедегі мәндерді жою үшін қажет (олар бір-бірінен пиктограммалары арқылы ажыратылады). Барлық батырмалар бағдарламаның жұмыс үдерісінде белсенді болып табылады.

Сондыықтан, жоғарыда сипатталған басқару органдары жасанды серіктің физикалық моделін толық зерттеуге мүмкіндік береді. Зерттеу мақсатына сәйкес қажет мәндерді бере отырып, әртүрлі траекторияларды салып оларды жоюға болады.

Функция графиктері бар терезе және интегралдық нәтижелердің 1-кестеде әрбір траектория үшін басқарудың ешқандай органдары жоқ. Терезенің оң жағында 2-кестені тұрғызу үшін берілген кесетені салу үшін параметрлерді енгізуге арналған екі жол бар. Біріншісіне 2-кестенің бағандар саны енгізіледі, бұнда қажет сипаттамалар енгізіліп тұрады (берілген септе бұл сектордың ауданы). Ал екінші жолға уақыт мәндері беріледі. Осы уақыт мәнінен кейіін келесі мәндер кестеге жазылып отырады. Мысалы, 0,1, 0,2, …, 1 уаақыт мәндері үшін траекторияның 10 нүктесі енгізііледі.

«Қорытындыы график» терезесінде 1-кестенің екі бағаны бойынша функцияның графигін тұрғызуға болады. Бағандар нөмері бағдарламаның негізгі модулінде көрсетілген. Графикті тұрғызу «Салу» батырмасын басу арқылы жүргізіледі. Осы терезенің басқа батырмасы арқылы «көпіршіктердің» өлшемі басқарылады. Бағдарламаның барлық жұмысында екі батырма да белсенді жұмыс жасайды.

Delphi тілінде модельдеу эксперименті.

Жасанды серіктің қозғлыысының эксперименттік зерттеуін жүргізелік. Сандық экспериментті жүргізу үшін әуелі dt уақыты бойынша қадамды таңдау қажет. Оның мәні жылдамдықты есептеу кезінде үдеудің өзгересін және жаңа координатты есептеуде жылдамдықтың өзгерісін ескермес үшін өте аз болу керек. Бірақ өте аз да болмауы қажет, себебі бұл кезде траекторияны салу үшін көп уақыт қажет болады. Масштаб ретінде біз жүйенің сипаттамалық параметрлерін таңдағандықтан, жүйенің типтік уақыт интервалы бірге тең. Сондықтан dt уақыт аралығы бірден кіші болуы тиіс; мысалы оны 0,01 деп алайық. Енгізу қажет екінші параметр ол бастапқы жылдамдық. Тағы да есептеу есептің меншікті масштабында жүргізілетіндіктен бірініші эксперимент үшін V0 = 1 деп қабылдаймыз. Енді «Счет-1» батырмасын басу арқылы бір траекторияны алуға болады. Алынған траекторияны қарастыралық. Ол шеңберге ұқсас, бірақ жасанды серіктің тартылыс центрін айналуы кезінде траектория тұйықталмайды (3-суреттегі графиктің ішкі қисығы). Бұл есептеудің жеткіліксіз дәлдікпен жүргізілгеніне байланысты. Енді dt шамасын екі есе азайтайық: dt = 0,005 және қисық түсін өзгертелік. Әртүрлі dt үшін алынған нәтижелерді салыстыруға болады. «Счет-1» батырмасын басамыз. Нәтиже жақсарды, бірақ әлі де өте аз қадам қажет. Ал dt = 0,001 деп есептесек, траектория тұйықталады. Егер  тұрғызылған қисықтың интегралдық сипатына көңіл аударсақ (3-суреттегі 1-кесте), онда е эксцентриситетті есептеу дәлдігінің артуымен кеміп және нөлге жуықтағанын көреміз. Уақыт аралығы dt –ны 0,0001-ге дейін азайтайық. Жаңа түсті және «Счет-1» батырмасын басамыз. Енді эксцентриситет 0-ге тең, үлкен жарты өсі 1-ге тең деп алсақ, онда траектория шеңбер болады. Алынған бірліктерде бірінші ғарыштық жылдамдық 1-ге, ал айналу периоды 2p-ге тең. Төменгі кестеден осы траектория үшіін Кеплердің екінші заңының дұрыстығына көзімізді жеткіземіз.

 

3-сурет. dt әртүрлі мәндері үшін алынған эксперимент нәтижелері.

 

Жасанды серіктің траекториясы тағы қандай болуы мүмкін деген сұрақ туады. Сөйтіп 1-ден 2-ге дейін бастапқы жылдамдықтарды өзгерте отырып, траекторияны салайық. Графикалық жолды және кестені тазалап, қажет мәндерді таңдап, «Счет-М» батырмасымен бағдарламаны жүргіземіз. Сонда 4-суретте осы эксперименттің нәтижелері көрсетіледі. Бастапқы жылдамдық мәнінің өсуімен, эллипс х осі бойымен тартылатынын көреміз. Тартылыс центрі (координат басы) эллипстің оң фокусында орналасқан. Соңғы тұйықталған траектория V0 = 1,4 мәні кезінде алынған (ол күшті созылып, экранға сыймаған). Бұл траектория үшін эксцентриситет 1-ге тең, яғни оған сәйкес бастапқы жылдамдықтың мәні екінші ғарыштық жылдамдыққа жуық. Кестелердегі алынған мәндер Кеплердің екінші және үшінші заңдарының орындалатындығыын көрсетеді.

 

 

4-сурет. Траектория серияларын есептегеннен кейінгі нәтижелер терезесінің қалпы.

 

Эксперимент соңында «Қорытынды график» терезесінде жасанды серіктің айналу периодының оның бастапқы жылдамдығына тәуелділік графигін тұрғызамыз. Бұл қисық 2-суретте көрсетілген.

Қолданылған әдебиеттер:

1. Коткин Г. Л., Черкасский В. С. Компьютерное моделирование физических процессов с использованием MATLAB: Учеб. пособие / Новосиб. ун-т. Новосибирск, 2001. 173 с.

2. Хуторова О.Г., Стенин Ю.М., Фахртдинов Р.Х., Морозова Л.В., Журавлев А.А., Теплов В.Ю., Зыков Е.Ю. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ. Методическое пособие.- Казань.-2001, 50 с.