Линейная задача терминального управления.

Институт Энергетики Таджикистана

Тагайназаров С.

1. Математическая модель. Пусть заданы: 1). динамическая система управления

(1)

2). класс доступных управлений, состоящий из кусочно-постоянных функций , стесненных ограничением .

3). терминальное множество в пространстве состояний

(2)

4). многогранный шар радиуса :

назовем -окрестностью терминального множества.

Предположим, что множество достижимости принадлежит конечной окрестности терминального множества (2): .

Линейная задача терминального управления в геометрической формулировке: среди точек множества найти такую , которая лежит в минимальной окрестности множества :

при (3)

В аналитической форме рассматриваемая задача имеет вид:

(4)

Поскольку в рассматриваемой задаче (4) нет терминальных ограничений, то любое доступное управление назовем допустимым управлением.

Минимальное число , при котором -окрестность терминального множества содержит состояние , порожденное допустимым управлением , назовем значением критерия качества задачи (4) на допустимом управлении .

Определение 1. Допустимое управление , будем называть оптимальным, если .

Определение 2. При заданном числа допустимое управление , называется -оптимальным, если оно удовлетворяет неравенству: .

1. Опора. Опорное управление. Пуст -произвольное подмножество множества . На отрезке выбираем конечное множество моментов . Введем множества . Количество элементов во введенных множествах подберем так, чтобы выполнялось равенство:

Рассмотрим два случая: 1). , 2). .

Сформируем множество

где -дополнительный индекс, соответствующий переменной .

Обозначим , я строка матрицы .

Построим матрицу , с блоками

Определение 3. Совокупность назовем опорной задачи, если невырождена опорная матрица .

Обозначим .

Определение 4. Пара из допустимого управления и опоры называется опорным управлением. Опорное управление назовем невырожденным, если :

1). Значения управления в опорные моменты некритические:

2). терминальное состояние , порожденное этим управлением, вместе с удовлетворяет неравенствам:

2. Формула приращения критерия качества. Пусть -опорное управления

Обозначим .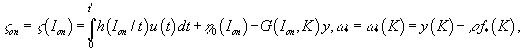

Наряду с допустимым управлением с и рассмотрим тройку , удовлетворяющую для выбранных равенствам

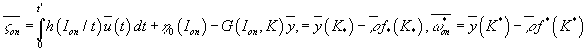(2)

Найдем приращение критерия качества задачи (4) при переходе от опорного управления к управлению .

Обозначим ,

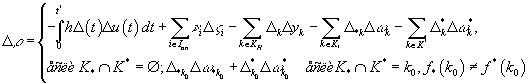
Теорема (критерия оптимальности). Для оптимальности допустимого управления , достаточно выполнения соотношений:

1) если -опора первого типа, то

при ; при ; при ; при ; при ; при ; при ; при ; при ; при ; при .

2) если -опора второго типа, то

при ; при ; при ; при .

Пусть -невырожденное опорное управление. Тогда условия (1), (2) необходимы для оптимальности управления .

Литература.

1. Габасов Р., Давронов Б.Э., Тагайназаров С., Хритоненко Н.В. Адаптивный метод решения интервальной задачи линейного программирования. Ч.П. Алгоритм. Минск, 1989. -45с. –библиогр.: 3 назв. -/БГУ им. В.И.Ленин. Деп. в ВИНИТИ 14.02.89.

2. Тагайназаров С. Оптимальное управление линейной системой в условиях неопределённости. Минск, 1989. -40 с. –Библиогр.: 5 назв. -/БГУ им. В.И.Ленин. Деп. в ВИНИТИ 28.02.89.