д.ф.м.н. Сафаров Д.С. и
Саидназаров Р.
Кургантюбинский
госуниверситет Республика Таджикистан
Двоякопериодические
решения одного класса
эллиптических систем
второго порядка
На
комплексной плоскости ![]() рассмотрим эллиптическую систему, записанную
в комплексной форме
рассмотрим эллиптическую систему, записанную
в комплексной форме ![]()
![]() (1) где
(1) где ![]()
![]() дифференциальный оператор Бицадзе,
дифференциальный оператор Бицадзе, ![]() постоянные комплексные числа,
постоянные комплексные числа, ![]() заданная функция.
заданная функция.
В монографии ![]() , для уравнения
, для уравнения
![]() ,
(2) показано, что однородная задача Дирихле в круге
,
(2) показано, что однородная задача Дирихле в круге ![]() , не будучи ни фредгольмовой, ни нетеровой, нормально
разрешима по Хаусдорфу. Однородное уравнение (2) имеет бесчисленное
множество решений, а для разрешимости
неоднородного уравнения необходимо и достаточно выполнения бесчисленных
множеств условий ортогональности.
, не будучи ни фредгольмовой, ни нетеровой, нормально
разрешима по Хаусдорфу. Однородное уравнение (2) имеет бесчисленное
множество решений, а для разрешимости
неоднородного уравнения необходимо и достаточно выполнения бесчисленных
множеств условий ортогональности.
Теория уравнения более общее чем
уравнения (1) связаны с теории полианалитических функций, для которых И.Н.
Векуа ![]() разработал
эффективные методы их изучения.
разработал
эффективные методы их изучения.
Некоторые результаты касающиеся
полианалитических функций порядка ![]() , полученные в последние ряда лет приведены в обзорной
стати М.Б.Балка
, полученные в последние ряда лет приведены в обзорной
стати М.Б.Балка ![]() .
.
Заметим, что переход от аналитических
функций к полианалитическим функциям
порядка ![]() сопровождает
существенными качественными изменениями в свойствах таких функций. Так,
например не сохраняется теорема Лиувилля, теорема единственности, принцип
максимума. Тем не менее, для таких функций доказывается «Ослабленный вариант»
принципа максимума теорема единственности,
более подробно можно ознакомится в работе
сопровождает
существенными качественными изменениями в свойствах таких функций. Так,
например не сохраняется теорема Лиувилля, теорема единственности, принцип
максимума. Тем не менее, для таких функций доказывается «Ослабленный вариант»
принципа максимума теорема единственности,
более подробно можно ознакомится в работе ![]() .
.
Теория полианалитических функций
порядка ![]() связано с
теории аналитической функций двух независимых комплексных переменных и их свойства на неаналитической поверхности. При
связано с
теории аналитической функций двух независимых комплексных переменных и их свойства на неаналитической поверхности. При
![]() решение
однородного уравнения (1) назевается
бианалитической.
решение
однородного уравнения (1) назевается
бианалитической.
Для уравнения (1) мы будем исследовать
задачу существования и нахождения двоякопериодических решений с основными
периодами ![]() . Это задача для регулярных решений уравнения (1), то
есть решений класса
. Это задача для регулярных решений уравнения (1), то
есть решений класса ![]() , связано распространением теоремы Лиувилля, в случае
решений допускающих конечное число полюсов в конечной частью плоскости
, связано распространением теоремы Лиувилля, в случае
решений допускающих конечное число полюсов в конечной частью плоскости ![]() с
распространением теории эллиптических функций.
с
распространением теории эллиптических функций.
В данной работе мы дадим описание ядро и
коядро задачи в случае регулярных решений с применением теории эллиптических
функций Вейерштрасса ![]() .
.
Как в ![]() обозначим через
обозначим через
![]() класс (
класс (![]() пространство)
двоякопериодических функций с основными периодами
пространство)
двоякопериодических функций с основными периодами ![]()
![]() и принадлежащих
соответственно в
и принадлежащих
соответственно в ![]() , где
, где ![]() основной параллелограмм решетки периодов
основной параллелограмм решетки периодов ![]() . Тогда по теореме вложения
. Тогда по теореме вложения ![]() при
при ![]() ,
,![]() ,
,![]() пространство двоякопериодических функций
пространство двоякопериодических функций ![]() ,
для которых все производные порядка
,
для которых все производные порядка ![]() непрерывны по
Гельдеру с показателем
непрерывны по
Гельдеру с показателем ![]() .
.
Предположим, что ![]() и будем искать
решения (1) из
и будем искать
решения (1) из ![]() . Структуры решений однородного уравнения (1) и её
разрешимости зависят от расположения корней уравнения
. Структуры решений однородного уравнения (1) и её
разрешимости зависят от расположения корней уравнения
![]() .
(3)
.
(3)
Легко видеть, что для решений
однородного уравнения класса ![]()
![]() справедливо.
справедливо.
Лемма 1. Пусть ![]() корны уравнения
(3). Тогда любое решение однородного уравнения (1) представимо в виде
корны уравнения
(3). Тогда любое решение однородного уравнения (1) представимо в виде
![]() , (4) где
, (4) где ![]() произвольные
аналитические функции в область
произвольные
аналитические функции в область ![]() .
.
Лемма 2. Если ![]() корны уравнения
(3), то справедливо представление
корны уравнения
(3), то справедливо представление
![]() (5)
(5)
![]() произвольные
аналитические функции.
произвольные
аналитические функции.
Эти формулы связывают класс
двоякопериодических решений однородного уравнения с классом двоякопериодических функций второго рода с
периодами ![]()
![]() .
.
Пусть ![]() решетка вида
решетка вида
![]()
![]() .
.
Из
свойства эллиптических функций ![]() получим
получим
Лемма 3. Для того чтобы однородное уравнение (1) в классе ![]() допускало
нетривиальное решение необходимо и достаточно, чтобы хотя бы
допускало
нетривиальное решение необходимо и достаточно, чтобы хотя бы ![]() или
или ![]() , при этом
, при этом
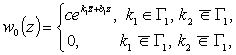
где
![]() постоянное, а число
постоянное, а число ![]() удовлетворяет
условию
удовлетворяет
условию
![]() .
.
Теперь разыскиваем решения неоднородного
уравнения, в случае различных корнях уравнения (3), в виде
![]() , (6) где
, (6) где
![]() пока
неизвестные функции.
пока
неизвестные функции.
Подставляя (6) в (1) и используя
результаты работы ![]() , получим.
, получим.
Теорема 1. Пусть
![]() различные корны уравнения (3) и
различные корны уравнения (3) и ![]() . Тогда однородное
уравнение имеет два решения, а для разрешимости неоднородного уравнения
необхидимо и достаточно, чтобы
. Тогда однородное
уравнение имеет два решения, а для разрешимости неоднородного уравнения
необхидимо и достаточно, чтобы
![]() , (7) где
, (7) где ![]() как в лемме 3. При этом все решения
уравнения (1) из класса
как в лемме 3. При этом все решения
уравнения (1) из класса ![]() представимы в виде
представимы в виде
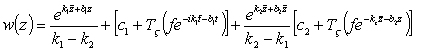 ,
,
где
![]() произвольные постоянные,
произвольные постоянные, ![]() интегральный оператор с
ядром
дзета – функция Вейерштрасса
интегральный оператор с
ядром
дзета – функция Вейерштрасса ![]()
![]() .
.
Свойства
интегралного оператора изученно в ![]() ,
,![]() ,
,
 .
.
Теорема
2. Пусть ![]() . Тогда для разрешимости
уравнения (1) небходимо и достаточно лишь выполнении первого условия (7) при
. Тогда для разрешимости
уравнения (1) небходимо и достаточно лишь выполнении первого условия (7) при ![]() . При этом решения
уравнения (1) представимы в виде
. При этом решения
уравнения (1) представимы в виде
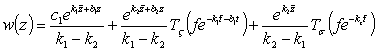 ,
,
где
![]() произвольная постоянная,
произвольная постоянная, ![]() как в теореме
1, а
как в теореме
1, а ![]() интегральный оператор с
ядром
интегральный оператор с
ядром![]() сигма – функция
Вейерштрасса
сигма – функция
Вейерштрасса
![]() .
.
Анологичная
теорема справедлива при ![]() .
.
Теорема
3. Пусть ![]() ,
, ![]() . Тогда уравнение (1)
при любой правой части имеет одно единственное решение вида
. Тогда уравнение (1)
при любой правой части имеет одно единственное решение вида
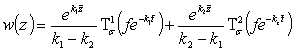 ,
,
где ![]() ,
, ![]() интегральные оператори вида
интегральные оператори вида ![]() соответетственно при
соответетственно при ![]()
![]() ,
, ![]() .
.
Теорема 4.
Пусть ![]() и
и ![]() . Тогда однородное
уравнение имеет одно решение, а для
разрешимости неоднородного уравнения необходимо и достаточно, чтобы
. Тогда однородное
уравнение имеет одно решение, а для
разрешимости неоднородного уравнения необходимо и достаточно, чтобы
![]()
где постоянное ![]() как в лемме 3. При этом все решения (1) имеют вид
как в лемме 3. При этом все решения (1) имеют вид
![]() ,
,
где
![]() произвольная постоянная, постоянное
произвольная постоянная, постоянное ![]() является
решением систем уравнений
является
решением систем уравнений

![]() ,
,
![]() циклические
постоянные функции
циклические
постоянные функции ![]() .
.
Теорема 5. Пусть ![]() .
Тогда уравнение (1) при любой правой части имеет только одно единственное
решение вида
.
Тогда уравнение (1) при любой правой части имеет только одно единственное
решение вида
![]()
где ![]() как в теореме 2, в котором
как в теореме 2, в котором ![]() .
.
Литература
[1] Бицадзе А.В. Некоторые классы уравнений в
частных производных, М; Наука 1981. 448с.
[2] Векуа И.Н. Новые методы решения
эллиптических уравнений. –М. – Л. : Гостехиздат, 1948г.
[3] Балк М.Б. Полианалитические функции. KOMPLEXE ANALYSIS AND IHER ANWENDUNG AUR PARTIELLE DIFFERENTIALGLET
CHUNGEN, 1980, /41(м/8)/ Halle c. 11 – 48.
[4]
Ахиезер Н.И. Элементы теории эллиптических функций, М., 1971г, 318 с.
[5]
Сафаров Д.С. О двоякопериодических обобщенных аналитических векторах. ДАН РТ,
т. 24, №9, с. 141 – 144.
[6]
Сафаров Д.С. Двоякопериодические обобщенные аналитические функции.
Дифференциальные уравнения. 1991г, т. 27, №4,
с. 656 –664.