Математика/5. Математическое моделирование

Студентка Васильева Т.М.

Северо-Казахстанский Государственный Университет имени Манаша Козыбаева, г. Петропавловск, Республика Казахстан

Методы решения задач оптимизации

Учебная нагрузка профессорско-преподавательского состава – это все виды занятий со студентами в аудитории, руководство практикой, руководство аспирантами, проверка контрольных работ, руководство и прием курсовых и дипломных проектов, консультации, прием зачетов и экзаменов, кураторство, участие в государственной аттестационной и экзаменационной комиссии.

Расчет учебной нагрузки кафедры и ее распределение между преподавателями – одна из ответственных, но достаточно трудоемких обязанностей заведующего кафедрой вуза, особенно если велико число дисциплин, читаемых на кафедре, а кадровый состав на кафедре достаточно многочислен и динамичен.

Специфика работы преподавателя вуза не позволяет руководствоваться при распределении нагрузки классической технологией тайм-менеджмента, поскольку она не укладывается в обычные рамки «с 8 до 17». Это связанно с особенностями расписания учебных занятий, предметами, которые он преподает, различные способы подачи материала предполагают даже для одной и той же дисциплины различное время подготовки, способы контроля усвоения знаний также могут быть различны - от тестового контроля знаний до классического экзаменационного опроса по билетам или творческого задания, а также «внеучебной» нагрузкой, которая, как правило, включает в себя как воспитательную, так и научную деятельность. Поэтому необходимо определиться с методом решения задачи по оптимизации нагрузки на профессорско-преподавательский состав кафедры.

Генетический алгоритм – новейший, но не единственно возможный способ решения задач оптимизации. С давних пор известны два основных пути решения таких задач – переборный и локально-градиентный. У этих методов свои достоинства и недостатки, и в каждом конкретном случае следует подумать, какой из них выбрать.

Следует рассмотреть достоинства и недостатки стандартных и генетических методов на примере классической задачи коммивояжера. Суть задачи состоит в том, чтобы найти кратчайший замкнутый путь обхода нескольких городов, заданных своими координатами. Оказывается, что уже для 30 городов поиск оптимального пути представляет собой сложную задачу, побудившую развитие различных новых методов, в том числе нейросетей и генетических алгоритмов.

Каждый вариант решения – это числовая строка, где на j-ом месте стоит номер j-ого по порядку обхода города. Таким образом, в этой задаче 30 параметров, причем не все комбинации значений допустимы. Естественно, первой идеей является полный перебор всех вариантов обхода.

Переборный метод, в соответствии с рисунком 1, наиболее прост по своей сути и тривиален в программировании. Для поиска оптимального решения необходимо последовательно вычислить значения целевой функции во всех возможных точках, запоминая максимальное из них.

Рисунок 1. Переборный метод

Недостатком этого метода является большая вычислительная стоимость. В частности, в задаче коммивояжера потребуется просчитать длины более 1030 вариантов путей, что совершенно нереально. Однако, если перебор всех вариантов за разумное время возможен, то можно быть абсолютно уверенным в том, что найденное решение действительно оптимально [1].

Второй популярный способ основан на методе градиентного спуска в соответствии с рисунком 2. При этом вначале выбираются некоторые случайные значения параметров, а затем эти значения постепенно изменяют, добиваясь наибольшей скорости роста целевой функции. Достигнув локального максимума, такой алгоритм останавливается, поэтому для поиска глобального оптимума потребуются дополнительные усилия.

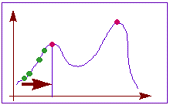
Рисунок 2. Метод градиентного спуска

Градиентные методы работают очень быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум [2].

Типичная практическая задача, как правило, мультимодальна и многомерна, то есть содержит много параметров. Для таких задач не существует ни одного универсального метода, который позволял бы достаточно быстро найти абсолютно точное решение.

Однако, комбинируя переборный и градиентный методы, можно надеяться получить хотя бы приближенное решение, точность которого будет возрастать при увеличении времени расчета в соответствии с рисунком 3.

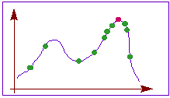
Рисунок 3. Зависимость точности расчетов от времени

Генетический алгоритм представляет собой именно такой комбинированный метод. Механизмы скрещивания и мутации в каком-то смысле реализуют переборную часть метода, а отбор лучших решений - градиентный спуск. В соответствии с рисунком 4 показано, что такая комбинация позволяет обеспечить устойчиво хорошую эффективность генетического поиска для любых типов задач.

Рисунок 4. Эффективность алгоритмов

Если на некотором множестве задана сложная функция от нескольких переменных, то генетический алгоритм - это программа, которая за разумное время находит точку, где значение функции достаточно близко к максимально возможному. Выбирая приемлемое время расчета, получается одно из лучших решений, которые вообще возможно получить за это время [3].

Литература:

1. Воронцов К.В., Методы оценивания и выбора моделей - Новосибирск, 2006. - 123 с.;

2. Пантелеев А.В., Летова Т.А., Методы оптимизации в примерах и задачах – Высшая школа, 2005. – 544 с.;

3. Панченко Т.В., Генетические алгоритмы – Астраханский университет, 2007. – 90 с.