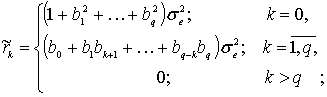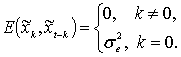Формализация кинетических процессов

формирования свойств материалов

Данилов А.М., д.т.н. проф., Гарькина И.А., д.т.н. проф.

Пензенский государственный университет архитектуры и строительства

Кинетические процессы как временные ряды. Определение устойчивости материала к длительному радиационному воздействию, установление остаточной прочности строительных материалов по годам эксплуатации, параметров разрушения декоративного покрытия и др. легко сводится к построению авторегрессионной модели кинетического процесса (случайного процесса ) со скользящим средним

(1)

на основе теории временных рядов [1].

Из (1) после умножения на и последующего усреднения получим

,

(2)

где . Таким образом, имеется только различных коэффициентов автокорреляции , значения которых непосредственно зависят от параметров скользящего среднего. Последнее разностное уравнение представляется в виде так называемого модифицированного уравнения Юла-Уолкера

.

(3)

Оценки параметров авторегрессии легко определить из (3) по вычисленным выборочным корреляционным функциям (оценки не являются эффективными). Чтобы оценить параметры скользящего среднего , сведем авторегрессионную модель (1) со скользящим средним к модели со скользящим средним вида

(4)

Для этого достаточно ввести

(равенство по определению). Здесь при определении из модифицированного уравнения Юла-Уолкера вместо теоретической корреляционной функции подставлена эмпирическая корреляционная функция .

Для автокорреляционной функции для справедливо:

(5)

Оценки параметров скользящего среднего и дисперсии оценок и определяются из (5). В соответствии с предыдущим справедливо

.

Приведем ряд частных случаев авторегрессионных процессов порядка с постоянными коэффициентами вида

.

Последнее выражение можно рассматривать как регрессию на со случайным остатком .

В простейшем случае получим марковский процесс . Обобщением является авторегрессионный процесс Юла .

Как и в марковском процессе предполагается независимость от и . Оценка коэффициента для модели порядка определялась по оценкам общего линейного авторегрессионного процесса порядка с использованием рекуррентной формулы (алгоритм Левинсона-Дурбина).

Правильность выбранного порядка модели определялась из условия

.

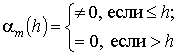Оценка порядка осуществлялась исходя из установленного предельного порядка модели, равного четырём. Определение коэффициентов модели осуществлялось по процедурам, приведенным в [2].

Кинетические процессы как решения обыкновенных дифференциальных уравнений. Формализация процессов формирования физико-механических характеристик материала осуществлялась на основе решения сначала общей, а затем и частной задач идентификации в классе обыкновенных дифференциальных уравнений. Оказалось, что для радиационно-защитных композитов формирование основных физико-механических характеристик материалов с достаточной точностью описывается в классе дифференциальных уравнений (в отклонениях от равновесного состояния ) второго порядка

. (6)

Параметрическая идентификация осуществлялась исходя из вида кинетических процессов и их характерных точек (начальные условия, установившиеся значения, точки перегиба, экстремума). Применение такого подхода во многом определялось возможностью формализации множества частных критериев для управления качеством материала на основе решения задач многокритериальной оптимизации.

Литература

1. Бокс, Дж. Анализ временных рядов. Прогноз и управление [Текст]: монография / Бокс Дж., Дженкинс Г. –М., 1974. – 405 с.

2. Данилов А.М. Математическое и компьютерное моделирование сложных систем [Текст] / А.М.Данилов, И.А.Гарькина, Э.Р.Домке // - Пенза: ПГУАС, 2011. - 296 с.