К.т.н. Бондаренко Д.А., к.т.н. Костюк Т.А., к.т.н. Старкова О.В.,
Салия М.Г.

Харьковский национальный университет строительства и архитектуры, Украина

Применение метода математического планирования эксперимента для оптимизации состава сухой строительной смеси

Большое число научных исследований в области современного строительного материаловедения посвящено высококачественным материалам для долговечного строительства. Высокие уровни технологических и эксплуатационных свойств конкурентоспособных материалов предполагают создание новых материалов с высоким качеством. Причем количество параметров качества может быть достаточно большим. Поэтому задачи проектирования сложных систем в частности проектирование сложных составов строительных смесей всегда многокритериальны, так как при выборе наилучшего варианта приходится учитывать много различных требований, предъявляемых к системе. Для решения такого вида задач нужно рассматривать совокупность критериев качества в координатах состава, параметров технологии и эксплуатации, используя для их анализа и оптимизации средства математического планирования эксперимента.

В [1] установлено, что совместное введение карбонатной добавки и стекловолокна способствует повышению прочности мелкозернистого бетона на сжатие и изгиб, что также обеспечивает повышение трещиностойкости за счет снижения усадочных напряжений при контракционном твердении в свежеуложенных цементных составах на подложках из «старого» бетона.

Целью настоящей работы является решение задачи оптимизации состава сухой строительной смеси путем введения карбонатной добавки и добавки стекловолокна и экспериментальное обоснование повышения прочностных показателей оптимизированного состава.

Оптимизацию состава сухой смеси проводили методами математического планирования эксперимента. В качестве оптимизируемых величин приняли предел прочности отвержденного состава при сжатии и изгибе. Процентное отношение расхода карбонатной добавки и добавки стекловолокна от количества цемента принимали на основании предварительных поисковых экспериментов. При этом расход химической добавки к цементу оставался постоянным.

Разработанный гидроизоляционный состав повышенной трещиностойкости по эксплуатационным характеристикам должен удовлетворять требованиям, предъявляемым к штукатурным составам.

В материаловедении и технологии базовыми экспериментально-статистическими моделями являются полиномиальные модели 2-го порядка:

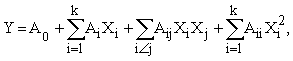
описывающие поверхности, образованные параболами. При этом разложении коэффициенты А_0, А_i, А_ij, А_ii эквивалентны частным производным ряда Тейлора для функции к-переменных

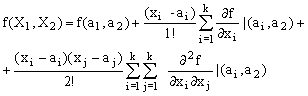
и равны

А₀ = ƒ(a₁,a₂),

A_i = ∂ƒ(a_1,a₂) / ∂x_i,

A_ij = 1/2! (∂²ƒ(a₁,a₂)) / ∂x_i ∂x_j,

A_ii = 1/2! (∂²ƒ(a₁,a₂)) / ∂x_i².

Таким образом, ковариационная матрица D = (x^Tx)^-1 не зависит от результатов эксперимента, может быть исследована до его реализации, позволяет определить численные значения вектора коэффициентов А для уравнения регрессии Ŷ и оценить характеристики модели и ее параметров. В данном случае планирование эксперимента по оптимизации гидроизоляционного состава повышенной трещиностойкости производили по плану полного факторного эксперимента ПЭФ 3^к, где к=2. Оптимальность такого плана заключается в том, что ковариационная матрица D, размером (к+1)∙(к+1) − диагональна, следовательно, все оценки коэффициентов независимы [2−4]. За переменный параметр х₁ принято процентное отношение расхода карбонатной добавки к цементу, а х₂ процентное отношение расхода стекловолокна к цементу. Пределы х₁ и х₂ приняты из условий задачи и ограничены прочностными показателями: 5<Х₁<15 и 0,02<Х₂<0,5. В экспериментально-статистическом моделировании принято переходить к безразмерным переменным:

x_i = (x_i-x_0i)/Δx_i,

где Δx_i = 0,5 (x_imax – x_imin); x_0i = 0.5 (x_imax + x_imin), что позволяет трансформировать трехфакторную призму в куб с вершинами (±1; ±1; ±1). В ходе эксперимента было проведено N=9 число опытов с m=2 числом повторений каждого.

Средние значения по результатам эксперимента (Y_μ и Y_λ) и расчет вспомогательных величин для оценки коэффициентов уравнения b₀, b_i, b_ii и b_ij приведены в табл. 1.

Уравнение регрессии для предела прочности при сжатии принимает вид:

Ŷμ = 26,5 – 2,63X₁² + 1,28X₁ – 0,73X₂².

Аналогично уравнение регрессии для предела прочности при изгибе:

Ŷλ = 9,35- 0,7X₁² +0,56∙X₁-X₂² +0.63X₂.

Адекватность моделей проверялась по критерию Фишера.

Поверхности отклика в трехфакторном пространстве (Ŷ, х₁, х₂) приведены на рис. 1 и 2.

Таблица 1

Расчетные значения для нахождения коэффициентов регрессии

№ опыта	ŷμ	ŷλ	ΔuYλ	Δu^2Yλ	ΔuYμ	Δu^2Yμ
1	21,8	6,4	2,3	5,29	0,4	0,16
2	25,8	7,7	2,7	7,29	1	1
3	24,4	7,5	3,3	10,89	1,2	1,44
4	22,6	8,0	3,6	12,96	1,7	2,89
5	26,5	9,35	1	1	0,05	0,025
6	25,1	9,2	1,8	3,24	0,3	0,09
7	21,8	7,6	2,3	5,29	0,4	0,16
8	25,7	8,9	2,7	7,29	1	1
9	24,4	8,8	3,3	10,89	1,2	1,44
				SSост=64,14 S^2ост=7,12 Sост=2,67 fост=9		SSост=8,205 S^2ост=0,91 Sост=0,95 fост=9

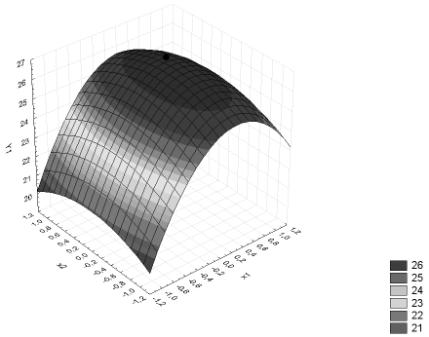
Рис. 1. Поверхность отклика отображающая зависимость предела прочности при сжатии Ŷμ от содержания карбонатной добавки Х₁ и добавки стекловолокна Х₂

Рис. 2. Поверхность отклика отображающая зависимость предела прочности при изгибе Ŷλ от содержания карбонатной добавки Х₁ и добавки стекловолокна Х₂

Из рис. 1 видно, что оптимальные значения Ŷμ находятся в окрестностях точки (0,8; −0,4), что соответствует 14 % содержания карбонатной добавки и 0,164 % стекловолокна от массы цемента соответственно. Предварительно по поисковым экспериментам предполагалось, что оптимум будет находится в пределах 10 % и 0,1 % соответственно.

Из рис. 2 видно, что оптимальные значения Ŷλ находятся в окрестностях точки (0,6; 0,4), что соответствует 13 % содержания карбонатной добавки и 0,356 % стекловолокна от массы цемента. Предварительно предполагалось, что оптимум будит находится в пределах 10 % и 0,1 % соответственно.

Из оптимизированного состава по содержанию карбонатной добавки и добавки стекловолокна были изготовлены образцы балочек и испытаны на прочность при сжатии и изгибе. Результаты испытаний представлены в табл. 3.

Таким образом, методом математического планирования эксперимента, подобран оптимальный состав сухой строительной смеси. При этом показатели прочности у оптимизированного состава выше, чем у состава, который был получен в результате экспериментальных исследований. Прочность при сжатии повысилась более чем на 50 %, а прочность при изгибе на 38 %.

Таблица 2

Результаты испытаний образцов

Наименование образцов	Предел прочности при сжатии, МПа (среднее арифметическое из трех серий)	Предел прочности при изгибе, МПа (среднее арифметическое из трех серий)
Состав до оптимизации: содержание стекловолокна − 0,1% содержание карбонатной добавки − 10% комплексная химическая добавка − 5%	26,2	7,1
Состав после оптимизации: содержание стекловолокна − 0,35% содержание карбонатной добавки − 13% комплексная химическая добавка − 5%	39,5	9,88

Литература:

1. Плугин А.А., Костюк Т.А., Салия М.Г., Бондаренко Д.А. Применение карбонатных добавок в цементных составах для гидроизоляционных и реставрационных работ зданий и сооружений // Сб. науч. трудов Института строительства и архитектуры. − М.: МГСУ, 2011. − Гл. 7. − С. 224−227.

2. Вознесенский В.А., Ляшенко Т.В., Огарков Б.А. Численные методы решения строительно-технологических задач на ЭВМ. − К.: Вища школа, 1984. − 328 с.

3. Вознесенский В.А. Статистические решения в технологических задачах. − Кишинев: Картя молдовеняскэ, 1969. − 231 с.

4. Вознесенский В.А. Статистические методы планирования эксперимента в технико-экономических исследованиях. − М.: Финансы и статистика, 1981. − 263 с.