Бабич Д.И.
Днепропетровский
национальный университет
Асимптотика собственных значений и собственных функций одной
начально-краевой задачи.
Исследуется задача о
продольных колебаниях стержня конечной длины 
с переменным поперечным
сечением. Рассматривается случай, когда левый конец стержня связан с грузом
массы m1, а по
правому, вначале свободному концу, произведен удар грузом массы m2.
Материал стержня
удовлетворяет закону Больцмана-Вольтерра, т.е., связь между напряжением и
деформацией в материале стержня определяется соотношением [1]
, (1)
здесь Е(х) – модуль упругости,
ε(х,t) – деформация, s(x,t) – напряжение рассматриваемой точки
в данный момент времени t.
Известно, что уравнение
продольных колебаний стержня переменного сечения имеет вид
(2)
где u = u(x,t) – смещение сечений стрежня, w = w(x) – площадь поперечного сечения, r = r(x) – плотность вещества стержня.
Деформация ε = ε(x,t) и смещение связаны соотношением
Учитывая условия,
налагаемые на концы стержня, граничные условия задачи имеют вид
(3)
(4)
Начальные условия такие:
(5)
где 
– скорость ударяющего тела.
Для дальнейшего
предположим, что функции E = E(x), w = w(x), r = r(x) положительны и имеют производные ІІІ-его порядка с полной ограниченной
вариацией на отрезке [0,l], а также функция φ = φ(t) имеет производную ІІІ-его порядка с полной ограниченной
вариацией в [0; +¥) и φ(0)>0.
Применяя к задаче (1) –
(5) метод разделения переменных, а также учитывая сумму ряда 
которая равна
где 
,
получим решение задачи (1) – (5) в виде рядов
(6)
(7)
(8)
где 
– собственные функции, соответствующие
собственным значениям ln краевой задачи
(9)
(10)
(11)
a 
– решение уравнения
(12)
при l = ln, удовлетворяющее условиям
Получены асимптотические формулы [2]
для 
(14)
(15)
где
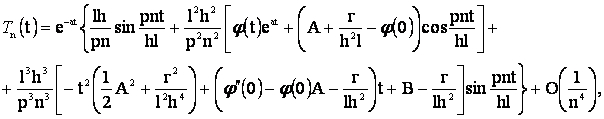(16)
где 
С помощью приведенной асимптотики для
проводится
исследование решения задачи (1) – (5).
Литература.
1. Качанов Л.М. Основы теории
пластичности. – М.: Гостехиздат, 1956. – 324с.
2. Левитан Б.М., Саргсян И.С. Введение в
спектральную теорию. – М.: Наука, 1970, 671с.