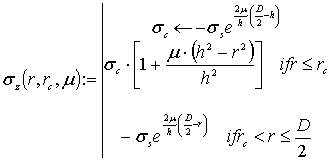Воскобойник Д.О.

Запорізька державна інженерна академія, Україна

ДОСЛІДЖЕННЯ МЕТОДОМ КІНЦЕВИХ ЕЛЕМЕНТІВ РОЗПОДІЛУ НАПРУГ НА КОНТАКТНИХ ПОВЕРХНЯХ ПРИ ОСАДІ ЦИЛІНДРІВ

Для визначення контактних напруг при осаді циліндричних заготовок розроблені кінцево-елементні моделі, які враховують фізико-механічні властивості тіл і тертя на поверхні контакту. Досліджені розподіли контактних напруг для різних співвідношень геометричних параметрів заготовок, відповідним до різних ступенів осадки.

Finite element models were developed to evaluate contact stress for cylindrical specimen under compression. Physical and mechanical properties of bodies and friction between them were accounted for by these models. Distributions of contact stresses for different ratio of geometry dimensions, correspondent to different levels of compression were under consideration.

Вступ

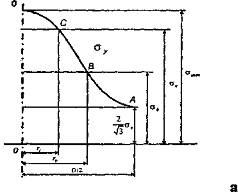
Контактні напруги, що виникають при осаді циліндрів, суттєво впливають на розвиток пластичного плину. Аналіз відомих експериментальних і теоретичних досліджень розподілу напруг на контактній поверхні у випадку пластичного деформування при вільнім осаджуванні металів, проведених поруч авторів [1,2] дозволяє зробити наступні висновки (схематичні криві розподілу контактних напруг для різних відношень d / h наведені на рис. 1).

1. Усі епюри нормальних контактних напруг, починаючи з відносини (d/h)≥4 випробовуваних зразків, мають куполоподібну форму.

2.       Для відношень (d/h)≥4 на ділянці АВ, якщо не враховувати невеликого піка на границі контактної площини, нормальні напруги зростають по кривій, увігнутій стосовно осі абсцис.

3.       На ділянці ВС (рис. 1а) нормальні напруги змінюються за лінійним законом. Довжина прямолінійних ділянок тим більше, чим більше відношення d / h. При досить малому відношенні d / h, прямолінійна ділянка пропадає й крива нормальних напруг складається із двох галузей - увігнутої й опуклої щодо осі абсцис (рис. 1б).

4.       У середній частині (поблизу осі симетрії відповідної до лінії розділу плину) крива розподілу нормальних напруг має куполоподібний характер, де криві плавно закруглюються, причому радіус закруглення тем менше, чим більше відношення d / h.

5.       При подальшому зменшенні відношення dlh крива нормальних напруг складається тільки з однієї опуклої щодо осі абсцис лінії, як це схематично показане на рис. 1в       .

Визначення епюр контактних напруг проводили також автори [3], причому отримані ними криві розподілу нормальних напруг якісно відповідають кривим, отриманим авторами [1, 2], тобто напруги в центральній зоні перевершують напруги в периферійних галузях контактної площини. Однак, автори [3] зазначають, що такий тип кривих відповідає лише зразкам з відношенням (d/h)≥4, а також значним ступенем деформації. Однак, при ступенях деформації менш 30% епюри розподілу нормальних напруг можуть також мати вигнений характер, тобто напруги в периферійних галузях більше, ніж у центральних.

(1)

                    (2)

                                  (3)

 

Рис. 1 - Схематичні криві контактних напруг при різних ступенях осадки a) d/h>4,       б) 2<d/h<4, в) d/h<2.

 

Чисельне моделювання

Моделювання осаду пружно-пластичних тіл - фізично нелінійне завдання механіки деформованого твердого тіла з геометрично нелінійними граничними умовами на поверхні контакту. Для опису взаємодії заготовки із частинами штампа використані наступні контактні умови: кінематична умова непроникнення, умова рівності нормальних контактних зусиль плит штампа й заготовки, і наявність дотичного зусилля, обумовленого тертям між контактуючими тілами, що підкоряється закону Кулона.

Чисельне моделювання процесу осадки циліндричних заготовок виконане методом кінцевих елементів за допомогою про­грамного пакету ANSYS (навчальна версія). Силова та геомет­рична симетрії послужили підставою для застосування двохмірної осі симетричної постановки. Для моделювання МКЕ циліндричної заго­товки, аналогічно від­працьованому тестовому завданню [4], були використані елементи типу PLANE 162, що допускають розв'язання завдання в осі симетричній постановці. Для чисельного опису ме­ханічних властивостей ма­теріалу прийнята ізотропна модель із білінійним законом де­формаційного зміцнення. Фізичні ха­рактеристики сталі 34ХН1М у нагрітому до1200°C стані задані наступними значеннями: щільність-7800 Кг/м3, коефіцієнт Пуассона-0,32, модуль пружності-150000 МПа, модуль зміцнення-0,4 МПа, границя текучості-60 МПа.

Лінеаризація діаграми «напруга - деформація» для обраної моделі проводиться за допомогою рівняння (4):

,                                                        (4)

де - межа текучості;  - модуль пластичного зміцнення; - модуль пружності, модуль зміцнення; - пластичні деформації.

Перехід до зони пластичного плину здійснюється при виконанні умови пластичності Мізесу 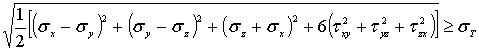(5):

         (5)

Деформування заготовки здійснюється шляхом завдання переміщень вузлам торцевих поверхонь верхньої плити штампа по вертикальній осі Y на величину відповідну заданого ступеня деформації. Переміщення вузлів плити в інших двох напрямках задані нульовими. Рух нижньої плити обмежене у всіх напрямках аналогічним способом. Деформації частин штампа в процесі осаду в порівнянні з деформаціями заготовки знехтуємо малі, тому плити штампа прийняті твердими тілами.

Таблиця 1

№ досліду

Інтервал

dк, мм

hк, мм

ε,%

1

1

24,6

35,7

22,6

24,6

1,6

2

1

50,6

14,8

44,8

50,6

3,03

3

1

75

7,5

61,08

75

8,14

 

Для дослідження зміни характеру кривої контактних напруг, залежно від відносин геометричних розмірів кування, змодельоване обтиснення зазначеної вище заготовки на наступні ступені осаду 24,6%, 50,6%, 75% (табл. 1).

Зміна виду кривих контактних напруг пояснюється тим, що при малих ступенях деформації частина обсягу деформується пластично, у той час як у інших частинах об'єму протікають пружні або пружно-пластичні деформації, на підставі проведених чисельних досліджень відзначено, що контактні напруги визначають розвиток зон пластичної деформації в обсязі деформуємого металу.

 

 

 

 

 

 

 

 

 


Рис. 2 - Епюри нормальних напруг при ступені осаду ε = 24,6 %.

 

Рис. 3 - Епюри нормальних напруг при ступені осадки ε = 50,6 %.

1. Для порівняння отриманих МКЕ епюр нормальних напруг з рішеннями авторів [1,2] аналогічних випадків осадки, на рис. 2-4 наведені криві розподілу нормальних напруг, побудовані за аналітичними залежностями (1-3). Аналіз отриманих результатів чисельних експериментів дозволяє зробити наступні висновки. У процесі навантаження спостерігається зміна поведінки епюр нормальних контактних напруг, зокрема, перехід від увігнутого виду кривої при d/h = l,6, через криву опуклого характеру при d/h = 3,03, до кривої куполоподібної форми при      d/h = 8,14.

2. При ступенях осадки 50,6% і 75% характер розподілу нормальних напруг експериментальної та теоретичної кривих однаковий, при цьому максимальна розбіжність отриманих результатів складає 16%.

 

 

 

 

 

 

 

 

 

Рис. 4 - Епюри нормальних напруг при ступені осадки ε = 75 % .

3. Пікові значення напруг на осі кінцево-елементної моделі заготовки обумовлені погрішністю контактного алгоритму, викликаний кінематичною умовою симетрії елементів. Описана похибка стає незначною при збільшенні щільності кінцево-елементної дискретизації близько осі симетрії. У розглянутих випадках викривлення епюри нормальних напруг з описаної причини відбувається на досить малій відстані, що дорівнює ширині одного кінцевого елемента від осі симетрії, і не виявляє істотного впливу на загальний вид кривих нормальних напруг

4. Епюра нормальних напруг при осаді на 24,6% кінцево-елементної моделі циліндра, на відміну від епюри, побудованої по теоретичній залежності (3), має ввігнутий характер.

Різна поведінка епюр пояснюється тим, що при виводі теоретичної залежності розподілу нормальних напруг для даного ступеня осаду автори [1,2] припускали присутності в повному обсязі деформуємого металу зон пластичної деформації. При аналізі отриманих МКЕ результатів з'ясувалося, що в цьому випадку поряд із пластичною деформацією мають місце пружно-пластичні деформації.

Для перевірки отриманого висновку про ввігнутий характер епюри розподілу нормальних напруг на контактній поверхні сталевого циліндра, побудовані епюри розподілу нормальних напруг на поверхні контакту, розраховані по теоретичній залежності (6) і отримані методом кінцевих елементів при ступені осаду ε = 3 % (рис. 5), відповідних до відсутності розповсюджених зон пластичного плину. Теоретичний розподіл контактних зусиль у пружній постановці для обмеженого майданчика контакту (r ≤ 0,8R) з достатнім ступенем точності може бути аппроксимовано за допомогою розв'язку завдання контакту циліндра й пружного півпростору [5] у наступному виді:

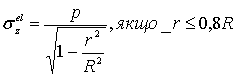                                             (6)

де р - тиск на осі симетрії циліндра.

У роботі [5] показаний несуттєвий вплив дотичних зусиль на розподіл тисків по контактній поверхні в пружній постановці, а отже про застосовність даного розв'язку до завдання контакту штампу з підставою без проковзування на початкових етапах деформування.

Тиск на осі циліндра визначене з розв'язку системи рівнянь (7):

                                           (7)

Тиск на осі циліндра становить р = 3,76·107 Па, при зусиллі               Р(р) = 36500 Н, відповідному до даного випадку опади.

Порівняння отриманих кривих розподілу контактних напруг у пружній постановці (рис. 2) показує, що їх характер однаковий, при цьому перехід пружних деформацій до пластичних походить від периферійних областей контактної поверхні до центру.

 

 

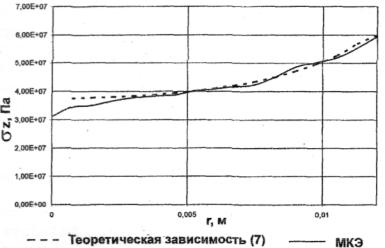
Рис. 5 - Розподіл нормальних напруг при ступені осадки ε = 3 %

 

На основі проведених досліджень вільного осаду циліндричних поковок зроблений висновок про наявність на контактній площині в загальному випадку трьох характерних зон: ковзання, гальмування й застою, усередині котрих контактні напруги залежать від певних закономірностей.

Висновок

У роботі виконане параметричне дослідження контактної взаємодії штампа й циліндра й, показане яким образом та при яких умовах у процесі осаду циліндра відбувається зміна характеру епюр нормальних напруг на контактній поверхні. Зокрема, підтверджене раніше висловлене припущення [3] про те, що при малих ступенях осаду напруги в периферійних областях контакту перевищують напруги, що виникають у центрі.

ЛІТЕРАТУРА

1. Унксов Е.П. Инженерная теория пластичности. — М. Машгиз, 1959. - 328 с.

2.    Теория обработки металлов давлением/ Под ред. И.Я. Тарновского — М.: Мепшллургиздат, 1963. -672с.

3.    Губкин СИ, Мицкевич Н.И. Распределение нормальных напряжений на контактной поверхности при свободном осаживании металлов. Сб. научных трудов (физ. техн. Ин-т АН Белорусской ССР), вып. 2, 1955, стр. 37-53.

4.    Шипуль О.В., Дыбский П.А., Мещеряков А.Н. Исследование параметров конечно-элементной модели при формоизменении осесимметричной заготовки.// Авиационно-космическая техника и технология. — 2004. — №5(13).-С. 18.

5.    Джонсон КС Механика контактного взаимодействия: Пер. с англ. - М. "Мир", 1989. —510 с.