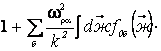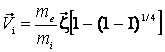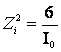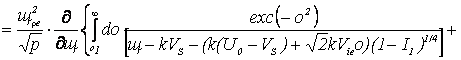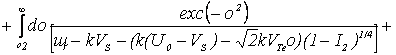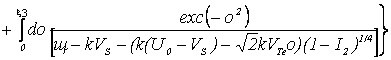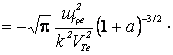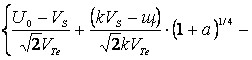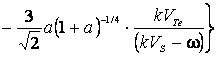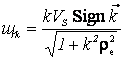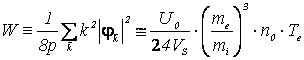В оргкомитет Интернет-конференции «Европейская наука XXI века»

Просим принять тезисы доклада «Турбулентная стабилизация ионно-звуковой неустойчивости» на секцию «Физика плазмы и плазменная технология».

Авторы: Сизоненко В.Л.

Коваленко Н.И.

УДК 533.9

Турбулентная стабилизация ионно-звуковой неустойчивости

Сизоненко В.Л., Коваленко Н.И.

Харьковский национальный аграрный университет им. В.В.Докучаева

При наложении на плазму сравнительно слабых внешних электрических полей скорость направленного движения электронов относительно ионов может стать значительно большей тепловой скорости ионов, но меньшей тепловой скорости электронов V_Те (U«V_Те). В этом случае в плазме возможна раскачка ионно-звуковых и ионно-циклотронных волн, которая теоретически исследовалась во многих работах [1] – [20]. В них изучались вопросы возбуждения и нелинейного насыщения колебаний, их влияние на электропроводность плазмы и др. Переход ионно-звуковой неустойчивости в ионно-циклотронную по мере уменьшения токовой скорости в слабо неизотермической плазме _с = (_і, возбуждение коротковолновых (·» 1, где – ларморовский радиус ионов, – волновой вектор) ионно циклотронных волн с частотами не близкими к – гирочастота ионов, n – целое число), квазилинейная динамика функции распределения частиц плазмы и спектрального распределения энергии колебаний при наличии токовых неустойчивостей, исследовались в работах [12 ], [18], [21] – [23 ].

Попытки развить нелинейную (квазилинейную) теорию динамики функции распределения заряженных частиц плазмы в среде турбулентных пульсаций электрического поля были осуществлены в работах [24 ] – [26]. Они стимулировали появление огромного количества работ и внесли свой позитивный вклад в развитие теории турбулентной плазмы. К сожалению, все эти работы обладали одним принципиальным недостатком: они не учитывали так называемый эффект уширения резонансов, связанный с нарушением условия Черенковского резонанса за счет колебаний частиц в электрических полях волн.

Попытку модернизировать квазилинейную теорию учетом уширения резонансов осуществили Дюпри [27 ], Орсзаг и Кришнан [28], Вейншток и Безерайдес [29]. [30]. Им пришлось применять громоздкий математический аппарат для отыскания приближенных решений кинетического уравнения Власова и использовать разумные допущения, превращающие, тем не менее, точные уравнения для функций распределения частиц в модельные. Важным (но не доказанным) допущением указанных работ являлось предположение о диффузном характере рассеяния частиц плазмы на турбулентных пульсациях электрических полей, позволявшее проводить статистические усреднения сложных интегро-дифференциальных операторов и феноменологически заменять их некоторыми коэффициентами диффузии ~.

Значительный прогресс в понимании механизмов уширения резонансов был достигнут в работах [31 ] – [33]. Здесь в [31 ], [32 ] показано, что если электрическое поле волн состоит из отдельных волновых пакетов, изменяющих свои фазы случайным образом на расстояниях L, значительно меньших длины пролета частицы, то скорости этих частиц состоят из суммы случайных величин. Вследствие этого, согласно центральной предельной теореме Ляпунова, хаотические части скоростей частиц имеют нормальные распределения, так что для отыскания усредненных характеристик движения частиц и амплитуд полей можно применять статистические усреднения. К сожалению, при выводе усредненных уравнений в работах [31], [32], были допущены неточности, а правильная система уравнений получена в [33]. Она имеет следующий вид:

, (1)

,

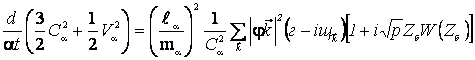где 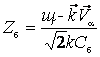, – функция Крампа и – электрический заряд и масса частицы, волновой вектор, – комплексная частота, состоящая из реальной и мнимой частей, , – Фурье-компонента потенциала электрического поля волн, – усредненная по статистическому ансамблю скорость частицы сорта , – усредненный по ансамблю квадрат хаотической скорости , α = (е, i) отмечает различные сорта заряженных частиц плазмы.

Одновременно с этим дисперсионное уравнение для колебаний имеет следующий вид:

= 0

(3)

где, – функция распределения частиц по скорости в начальный момент времени, , , равновесная плотность частиц сорта .

Нетрудно проверить, что уравнения (1) – (3) допускают закон сохранения энергии и импульса:

=

(4)

=

(5)

В настоящей работе с помощью уравнений (1) – (5) анализируется поведение ионно-звуковой неустойчивости, исследованной другими методами в многочисленных работах (см. выше).

Если взять ,

где и – средняя и тепловая скорости частиц в начальный момент времени, и положить , то из (3) получим, что

1+εi + εe = 0

(6)

ε_α ,

где , , , .

Для ионно-звуковой неустойчивости имеем: , , и из (6) получаем следующие выражения:

, ,

(7)

где 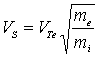, , , – скорость движения электронов относительно ионов.

Максимум при достигается для; .

Полагая в (1) , , , , получим, что

, ,

(8)

Аналогично, из (2) будем иметь:

, , .

(9)

Усредним теперь по начальному распределению. Тогда получим, что

,

(10)

где .

Из (10) следует, что условие выполняется, если . При этом тепловая энергия ионов (3/2) достигает величины , а значения и в (2) – величин:

; .

(11)

В принципе условие в выражениях (9) ничего существенно не изменяет. Поэтому ими можно пользоваться даже в случае . Тогда для отыскания воспользуемся условием , и получим, что

; εе.

(12)

В одномерном приближении выражение (12) сводится к следующим интегралам:

εе .

(13)

где

, ;

, ,

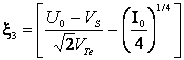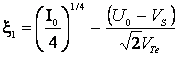при ; ,

, при .

В случае , беря в (13) только вычетные члены, получим, что

Іm εе ,

(14)

где . Добавляя теперь к (14) вещественную часть ε_е и полагая , будем иметь:

εе .

(15)

Тогда дисперсионное уравнение (3) примет следующий вид:

.

(16)

Из него находим частоту и инкремент колебаний:

, .

(17)

В случае справедливо: .

Тогда инкремент станет равным следующему выражению:

,

(18)

где , .

Из модельного уравнения

находим теперь поведение со временем:

,

(19)

где .

Как видим величина стремится к , т.е. происходит насыщение неустойчивости при следующей энергии колебаний:

,

(20)

где – температура электронов.

Нетрудно убедиться, что при уровне шумов (20) условие выполняется. При больших значениях последнее слагаемое в (14) всегда больше первого, так что неустойчивость отсутствует.

Сравним уровень (20) с тем, что получено в других работах для ионно-звуковой турбулентности, учитывавших нелинейное взаимодействие волн. В классических исследованиях Б.Б. Кадомцева и В.И. Петвиашвили [4], а также А.А. Галеева и Р.З. Сагдеева [34] рассматривалось нелинейное рассеяние волн на ионах плазмы. В результате эти авторы пришли к заключению, что должен установиться следующий уровень шумов:

(21)

Сравнивая (21) с (20), приходим к заключению что нелинейные процессы срабатывают при такой энергии колебаний, которая в 24 (m_i/m_е)^5/2 (Т_е/Т_i)~2 10^н раз превосходит наш уровень. Это значит, что большие усилия, затраченные специалистами на расчеты различных нелинейных взаимодействий оказались ненужными. Слишком высоким оказался и уровень шумов, полученный при учете нелинейного рассеивания ионно-звуковых волн на электронах [17] (W ~(m_е/m_i) n_o T_e ). В свое время он был отвергнут в работе [34] по той причине, что в [17] не учитывался эффект «уширения резонансов » для электронов. Но теперь оказалось, что и соображения А.А.Галеева и Р.З.Сагдеева на этот счет тоже были излишними [34].

В работах [1] – [26] – [34] на ионно-звуковую неустойчивость возлагались большие надежды как на причину появления аномального сопротивления плазмы с током. Приводились убедительные соображения на этот счет [34], но все они, как теперь понятно, оказались неверными. В самом деле, если усреднить выражение (8) для V_e по всем значениям, то окажется, что наша неустойчивость позволяет уменьшиться средней скорости электронов не более, чем на величину V~2U_o(I_o/4)^¼(m_e/m_i)^¾. Таким образом, ионно-звуковая неустойчивость не играет никакой роли в появлении аномального сопротивления плазмы, помещенной во внешнее электрическое поле.

Напомним, что результаты нашей теории относятся к случаю турбулентной плазмы. В действительности может происходить и возбуждение монохроматических волн во всем объёме плазмы, которые данная теория не описывает.

Литература.

1. Гордеев Г.В. ЖЭТФ, 27, 19, 1954.

2. Resenbluth M.N., Drummond W.E. Phys. Fl., 5, 1507,1962.

3. Ломинадзе Д.Г., Степанов К.Н. ЖТФ, 33, 1311, 1963.

4.Кадомцев Б.Б., Петвиашвили В.И. ЖЭТФ, 43, 2234, 1962.

5. Кадомцев Б.Б. Вопросы теории плазмы. – М.: Атомиздат, № 4, 1964. – С. 188.

6. Цытович В.Н. Нелинейные эффекты в плазме. – М.: Наука, 1967.

7. Sagdeev R.Z., Galeev A.A. Lectures on non – linear theory of Plasme. – Triest: 1966.

8. Силин В.П. ПМТФ, 1, 33, 1964.

9. Силин В.П., Горбунов Л.М. ДАН СССР, 145, 1265, 1962.

10. Коврижных Л.М. ЖЭТФ, 51, 1796, 1966.

11. Рудаков Л.И., Кораблев Л.В. ЖЭТФ, 50, 220, 1966.

12.Сизоненко В.Л., Степанов К.Н. ЖЭТФ, 49, 1197, 1965.

13. Кадомцев Б.Б., Погуце О.П. ЖЭТФ, 53, 2025, 1967.

14. Векштейн Г.Е. , Рютов Д.Д., Сигдеев Р.З. Письма ЖЭТФ, 11, 297, 1970.

15. Векштейн Г.Е. , Сигдеев Р.З. Письма ЖЭТФ, 11, 297, 1970.

16. Кингсеп А.С. ЖЭТф, 56, 1309, 1969.

17. 12.Сизоненко В.Л., Степанов К.Н. Письма ЖЭТФ, 9, 468, 1969.

18.Сизоненко В.Л., Степанов К.Н. УФЖ, 16, 438, 1971.

19. Каладзе Т.Д., Ломинадзе Д.Г., Степанов К.Н. УФЖ, 16, 469, 1971.

20. Ахиезер А.И., Ахиезер И.А., Половин Р.В., Ситенко А.Г., Степанов К.Н. Коллективные колебания в плазме. – М.: Атомиздат, 1964.

21. Сизоненко В.Л., Степанов К.Н. Известия Высших Учебных Заведений. Радиофизика, 15, 144, 1972.

22. Ранюк А.И., Сизоненко В.Л. ЖТФ, 44, 995, 1974.

23. Ломинадзе Д.Г., Сизоненко В.Л. ЖТФ, 44, 1839, 1974.

24. Веденов А.А., Велихов Е.П., Сагдеев Р.З. УФН, 73, 701, 1961.

25. Романов Ю.А., Филиппов Г.Ф. ЖЭТФ, 40, 123, 1961.

26. Drummond W.E., Pines D. Nucl. Fusion Suppl., Part 3, 1049, 1962.

27. Dupree T.H. Phys. Fluids, 9, 1773 (1966).

28. Orsag S.A. and Kraichnan R.H. Phys. Fluids, 10, 1720 (197 ).

29. Weinstock Terome. Phys. Fluids,12, 1045 (1969).

30. Weinstock Terome and Bezzerides B. . Phys. Fluids,16, 2287 (1973).

31. Сизоненко В.Л. // Матеріали III Міжнародної науково-практичної конференції „Науковий потенціал світу – 2006”, 18-19 вересня 2006 року. Том 9. – Дніпропетровськ: Наука і освіта, 2006. – С. 73-77.

32. Сизоненко В.Л. // Матеріали II Міжнародної науково-практичної конференції „Дні науки – 2006”, 17-28 квітня 2006 року. Том 34. – Фізика. - Дніпропетровськ: Наука і освіта, 2006. – С. 27-30.

33. Сизоненко В.Л. Нелинейное движение частиц плазмы в турбулентных электрических полях. Вестник Харьковского национального университета им. В.Н.Каразина, 2008 (в печати).

34. Галеев А.А., Сагдеев Р.З. Нелинейная теория плазмы. В кн. Вопросы теории плазмы. Вып. 7. – М.: Атомиздат, 1973. – С. 101.

Турбулентная стабилизация ионно-звуковой неустойчивости

Сизоненко В,Л., Коваленко Н.И.

Резюме

Изучено обратное воздействие колебаний плазмы на развитие ионно-звуковой неустойчивости в точной теории нелинейных процессов турбулентной плазмы. Показано, что стабилизация неустойчивости происходит при столь низком уровне шумов, что все работы предыдущих авторов в этом вопросе теряют силу.

Turbulent stabilization of ion-sound instability.

Sizonenko V.L., Kovalenko N.I.

Summary.

The riverse infuence of plasma fluctuations on ion-sound instability development has been researched in the precise theory of non-linear processes of turbulent plazma. It has been found out that stabilization of variability occurs at such low noise level, that the works by ofber authors concerning this problem lose any significance.