Петричкович
Александр Анатольевич
Закарпатский
Государственный Университет, Украина
Программа
управления фрезерным станком
В докладе рассматривается
процесс проектирования системы управления станком, готовая программа управления
станком и волновые алгоритмы.
Ключевые
слова: Жадный алгоритм,
Волновой алгоритм.
Постановка
задачи: создать компьютерную программу управления фрезерным
станком на базе трёх шаговых двигателей, принимающих управляющий сигнал с LPT-порта, которая позволяет делать точные
копии заданных рисунков в пространстве с заданным масштабом, скоростью,
глубиной и прочими параметрами.
Темпы экономического роста зависят от
машиностроения. Именно в нём материализуются основополагающие
научно-технические идеи, создаются новые орудия труда, системы машин, которые
определяют прогресс и в других отраслях. Закладываются основы широкого выхода
на принципиально новые технологии сохранения ресурсов, повышение продуктивности
труда и качества продукции.
Решение задач, повышение производительности
труда, а также улучшения качества продукции при минимальных затратах, связано с
широким внедрением станков с числовым программным управлением.
Копировальные станки с программным
управлением широко используются во многих отраслях промышленного хозяйства. Они
с высокой точностью и качеством выполняют такие операции, как: гравирование,
фрезерование, шлифование, лазерная,
плазменная, гидроабразивная резьба, выпаивание и другие.
Аналоги.
Любая информация по
проектированию подобных систем отсутствует, поскольку системы подобного рода
неплохо продаются и являются коммерческой тайной. Такие системы платные, имеют
богатую функциональность, но слишком громоздкие для обучения и работы.
Характеристики
разработанной программы.
Данная программа разработана на
языке программирования Delphi 7, имеет богатую функциональность и понятный
интерфейс, не требует слишком больших вычислительных ресурсов, работает
достаточно быстро и не является громоздкой по сравнению с аналогами. Даная
программа использует волновой алгоритмы.
Процесс
проектирования программы управления станком
Отбросим все лишние детали,
такие как работа с LPT-портом,
разработка интерфейса, реализация событий компонентов и прочие мелочи, которые
не имеют большой ценности, и рассмотрим проблему нахождения траектории движения
фреза с точки зрения математики.
Есть некоторое поле
размерностью m
x n, на котором расположены точки, в которых
необходимо сделать отверстие. Отверстия можно делать только в этих точках.
Первое, что приходит в голову,
— это реализовать тот же алгоритм, который используется в телевизорах и
мониторах для отсвечивания точек. Тогда получиться вложенный цикл типа «for x for y», в котором будет происходить поиск точки,
в которой нужно сделать отверстие. Всё очень просто, но в данном случае
траектория движения будет слишком длинной и время выполнения поставленной
задачи будет неприемлемо большим.
|
1 |
6 |
11 |
16 |
|
2 |
7 |
12 |
17 |
|
3 |
8 |
13 |
18 |
|
4 |
9 |
14 |
19 |
|
5 |
10 |
15 |
20 |
Пример поиск точек при использовании
первого алгоритма
Немного подумав, возникает идея
слегка изменить алгоритм и искать точки по принципу «змейки». Тогда у нас будет
цикл типа «for
x while y». Разница с первым алгоритмом лишь в том,
что теперь поиск в следующей вертикале будет начинаться с соседней точки. В
результате мы получим небольшое улучшение по времени выполнения поставленной
задачи, но даже в данном случае это слишком мало.
|
1 |
10 |
11 |
20 |
|
2 |
9 |
12 |
19 |
|
3 |
8 |
13 |
18 |
|
4 |
7 |
14 |
17 |
|
5 |
6 |
15 |
16 |
Пример поиск точек при использовании
второго алгоритма
Возникает вопрос: как сделать
так, что бы траектория движения была по возможности минимальной и сначала
проверялись бы точки, которые находятся ближе? Тогда, при наличии линий на
поле, траектория бы проходил по этим линиям.
|
1 |
3 |
|
|
|
2 |
|
4 |
|
|
|
|
|
5 |
|
10 |
9 |
|
6 |
|
11 |
|
8 |
7 |
Пример идеальной траектории
Сразу же возникает идея нарисовать
граф, вершины которого лежали бы в точках, в которых необходимо сделать
отверстие. Потом из каждой вершины провести рёбра ко всем остальным вершинам,
возле каждого ребра поставить число, которое бы означало цену перехода из одной
вершины в другую, которые соединяет это ребро. Остаётся только придумать
алгоритм, который бы из бесконечного числа всевозможных траекторий выбирал бы
одну единственную — идеальную траекторию. Это кажется фантастикой. Только поиск
такой траектории занял бы время намного большее, чем время выполнения
предыдущих двух алгоритмов. Я уже не говорю про количество вычислительных
ресурсов, которые бы потреблял этот зверь.
Этот вариант сразу же отпадает.
Создаётся впечатление, что это тупик. Но как же работают аналоги, по какому
принципу? Теперь я согласен на то, что траектория будет не идеальной, но время
выполнения все-таки должно быть приемлемым. Тогда это должен быть некий жадный
алгоритм, который ищет точку, время перемещения к которой должно быть
минимальным.
Но не нравится то, что для
каждой точки, в которой ещё нет отверстия, надо вычислять время перемещения. В
этом случае, при большом количестве точек, время выполнения поставленной задачи
будет большим, а хочется, чтоб точки находились практически сразу.
После нескольких дней обдумывания,
в голове нарисовался нужный алгоритм. Позже я узнал, что это известный
алгоритм, который является достаточно популярным, и называется волновым
алгоритмом.
|
1 |
3 |
|
|
|
2 |
|
4 |
|
|
|
|
5 |
|
|
7 |
6 |
|
|
|
8 |
9 |
10 |
11 |
Возможный вариант траектории при
использовании волнового алгоритма
Волновой алгоритм (Алгоритм Ли)
Волновой алгоритм является одним из самых уникальных
алгоритмов трассировки. Он позволяет построить трассу (путь) между двумя
элементами в любом лабиринте.
|
|
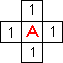
Из начального элемента распространяется в 4-х направлениях волна.
Элемент, в который пришла волна образует фронт волны. На рисунках цифрами
обозначены номера фронтов волны. |
|
|
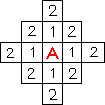
Каждый элемент первого фронта волны является источником вторичной волны.
Элементы второго фронта волны генерируют волну третьего фронта и т.д. Процесс
продолжается до тех пор, пока не будет достигнут конечный элемент. На втором этапе строится сама трасса. Её построение осуществляется в
соответствии со следующими правилами: 1.
Движение при построении трассы
осуществляется в соответствии с выбранными приоритетами. 2.
При движении от конечного элемента к
начальному номер фронта волны (путевые координаты) должны уменьшатся. |
Приоритеты направления движения выбираются на стадии
разработки. В зависимости от того, какими задаются эти приоритеты, получаются
разные трассы, НО длина трассы в любом случае остается одной и той же.
Преимущества волнового алгоритма в том, что с его
помощью можно найти трассу в любом лабиринте и с любым количеством запретных
элементов (стен). Единственным недостатком этого алгоритма является то, что при
построении трассы требуется большой объем памяти.
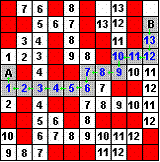
Пример использования ВОЛНОВОГО АЛГОРИТМА:
Красным цветом отмечены запрещенные элементы. Серым
цветом трасса после действия алгоритма.
А — начальная точка,
В — конечная.
Приоритеты движения ВЛЕВО, ВПРАВО, ВВЕРХ, ВНИЗ.
Построение трассы ведется от начальной точки к
конечной. Приоритетные направления показаны зелеными стрелками.
Выводы: Данная работа имеет
большую ценность в образовании и в науке. В ней описаны проблемы, с которыми
может столкнуться программист уже в реальных условиях работы. Также тут
рассматриваются разные способы их решения, их сравнение. Рассмотрен волновой
алгоритм, который является популярным, но в то же время он не изучается в
вузах. Указано, почему данный алгоритм является эффективным для поиска в
пространстве с преградами.
Литература
1.
http://ru.wikipedia.org/wiki/Шаговый
электродвигатель
2.
http://ru.wikipedia.org/wiki/Статор
3.
http://ru.wikipedia.org/wiki/Ротор (техника)
4.
http://ru.wikipedia.org/wiki/Жадный алгоритм
5.
http://www.firststeps.ru/theory/karta.html