Карачун В.В., Мельник В.М.
Національний технічний університет
України «КПІ»
МАЛІ КОЛИВАННЯ НАВАНТАЖЕНОЇ
НИТКИ
 Багато
важливих технічних проблем, зокрема,
динаміка елементів приладів, аналітично зводиться до вивчення коливань
гнучкої однорідної нерозтяжної нитки з вагою, що закріплена на її вільному
кінці, тоді як інший її кінець зафіксовано на нерухомій або пересувній опорі.
Багато
важливих технічних проблем, зокрема,
динаміка елементів приладів, аналітично зводиться до вивчення коливань
гнучкої однорідної нерозтяжної нитки з вагою, що закріплена на її вільному
кінці, тоді як інший її кінець зафіксовано на нерухомій або пересувній опорі.
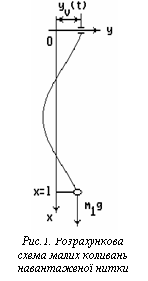
Диференціальне рівняння малих коливань нитки (рис.1) може бути представлене як -
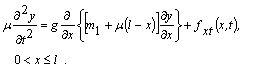 (1)
(1)
Якщо на нитці у точці ![]() закріплена вага
масою
закріплена вага
масою ![]() , тоді рівняння (1) буде справедливим тільки в межах
, тоді рівняння (1) буде справедливим тільки в межах ![]() ; вище точки закріплення цієї ваги, для ділянки
; вище точки закріплення цієї ваги, для ділянки ![]() , рівняння (1) змінюється, приймаючи форму -
, рівняння (1) змінюється, приймаючи форму -
![]() . (2)
. (2)
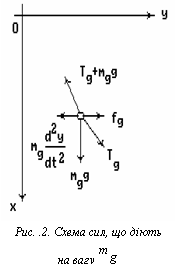
Щоб отримати диференціальне
рівняння, яке визначає рух власне ваги ![]() , розглянемо систему сил, включаючи силу інерції, прикладених до нього (рис.2).
, розглянемо систему сил, включаючи силу інерції, прикладених до нього (рис.2).
Тут ![]() - сила інерції,
- сила інерції, ![]() - вага вантажу,
- вага вантажу,![]() - зовнішня
сила, яка діюча на вагу.
- зовнішня
сила, яка діюча на вагу.
Дві сили, що
залишилися, являють собою натягнення нитки над вагою та під нею. Сума проекцій цих сил на вісь y
дає
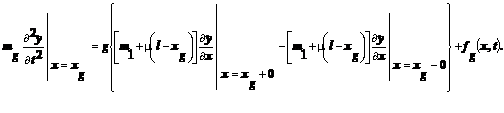 (3)
(3)
 Граничну
умову у верхній точці нитки
Граничну
умову у верхній точці нитки ![]() будемо розглядати як граничну умову I - го роду:
будемо розглядати як граничну умову I - го роду:
![]() . (4)
. (4)
Граничну умову в нижній точці ![]() отримуємо
шляхом розгляду суми проекцій сил, прикладених
до нижньої ваги, на вісь
отримуємо
шляхом розгляду суми проекцій сил, прикладених
до нижньої ваги, на вісь ![]() (рис. 3) -
(рис. 3) -
![]() , (5)
, (5)
де ![]() - зовнішня сила,
що діє на вагу
- зовнішня сила,
що діє на вагу ![]() ( направлена
вздовж осі
( направлена
вздовж осі ![]() ).
).
Початкові умови для нитки -
![]() ; (6)
; (6)
![]() (7)
(7)
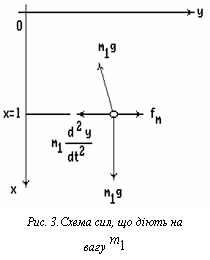
Для мас ![]() та
та ![]() умови їх
кріплення на нитці зводяться до умови неперервності нитки, а ось значення їх швидкостей за часу
умови їх
кріплення на нитці зводяться до умови неперервності нитки, а ось значення їх швидкостей за часу ![]() будемо вважати заданими окремо.
будемо вважати заданими окремо.
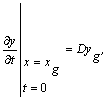 (8)
(8)
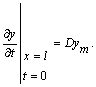 (9)
(9)
У випадку, наприклад, удару по одному
з вантажів (або по обох одночасно) їх
початкові швидкості можуть відрізнятися від початкових швидкостей відповідних
точок нитки.
Початкові і граничні умови, а також функції ![]() ,
, ![]() ,
, ![]() можуть
варіюватися в широких межах. Задаємо їх у вигляді підпрограм-функцій
можуть
варіюватися в широких межах. Задаємо їх у вигляді підпрограм-функцій
Function
Yn(X:real):real;
Begin Yn:=Ym*Х/lng
End;
Function
DYn(X:real):real;
Begin Dyn:=0
End;
Function
Yv(t:real):real;
Begin Yv:=Av*sin(Wv*t) End;
Function Fxt(S:integer;
t:real):real;
Begin Fxt:=Az*sin(Wz*t)-Kdy*(Yt[S]-Yp[S])/Tau End;
Function
Fm(t:real):real;
Begin Fm:=Am*sin(Wm*t)-Kdm*(Yt[m]-Yp[m])/Tau End;
Function
Fg(t:real):real;
Begin Fg:=Ag*sin(Wg*t)-Kdg*(Yt[Sg]-Yp[Sg])/Tau End;
У підпрограмі Fxt неперервна
змінна ![]() для зручності
подальшого використання замінена на її дискретний аналог S=round(X/h), де h крок по координаті (h=
для зручності
подальшого використання замінена на її дискретний аналог S=round(X/h), де h крок по координаті (h=![]() /m), m - число ділянок, на які розбивається нитка вздовж її довжини. Точно так
саме, в підпрограмах Fm і Fg сили опору, пропорційні швидкості руху відповідних вантажів, визначені через
дискретні аналоги похідних за часом.
/m), m - число ділянок, на які розбивається нитка вздовж її довжини. Точно так
саме, в підпрограмах Fm і Fg сили опору, пропорційні швидкості руху відповідних вантажів, визначені через
дискретні аналоги похідних за часом.
У загальному випадку
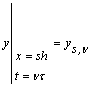 . (10)
. (10)
Значення y в поточний момент
часу ![]() зосереджені в
масиві Yt, якщо
зосереджені в
масиві Yt, якщо ![]() - в масиві Yp.
- в масиві Yp.
Поділимо в (1) всі члени рівняння на ![]() і продиференціюємо вираз в квадратних дужках -
і продиференціюємо вираз в квадратних дужках -
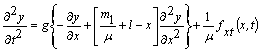 . (11)
. (11)
Перейдемо до дискретних змінних.
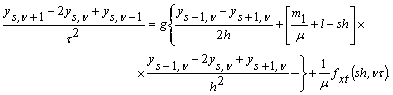 (12)
(12)
![]()
Тут Sg=round(Xg/h).
Розв’язуємо (12) відносно ![]() :
:
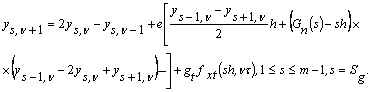 (13)
(13)
Зазначені у формулі коефіцієнти дорівнюють
![]() ;
; ![]() ;
;![]() ;
; ![]() .
.
Стосовно доданку, ![]() , то з метою забезпечення рівняння (13) справедливим не
тільки для ділянки нитки під вантажем
, то з метою забезпечення рівняння (13) справедливим не
тільки для ділянки нитки під вантажем ![]() , але і для ділянки
над ним, його обчислення оформлюється у вигляді підпрограми -
, але і для ділянки
над ним, його обчислення оформлюється у вигляді підпрограми -
Function
Gn(S:integer):real;
Begin
If S>Sg then Gn:=M1/Mu+lng
Еlse Gn:=(M1+Mg)/Mu+lng
End;
При наявності вантажу ![]()
![]() за умови
за умови ![]() , точка
, точка ![]() повинна «обслуговуватися» відповідно до
рівняння, яке в дискретній формі має вигляд -
повинна «обслуговуватися» відповідно до
рівняння, яке в дискретній формі має вигляд -
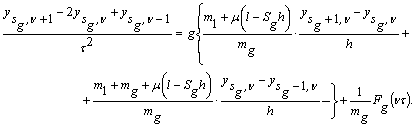
Розв’язуємо отримане
співвідношення відносно ![]() :
:
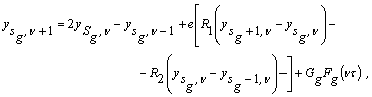 (14)
(14)
де 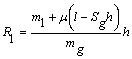 ;
; ![]() ;
; 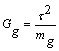 .
.
Для закріпленого
(верхнього) кінця нитки у відповідності з (4) маємо -
![]() . (15)
. (15)
Для нижнього кінця нитки ( для ![]() ), у
відповідності з (5), отримуємо:
), у
відповідності з (5), отримуємо:
![]() , (16)
, (16)
де 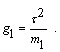
Якщо ![]() , тоді замість 16 знаходимо –
, тоді замість 16 знаходимо –
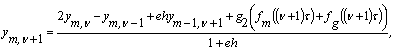 (17)
(17)
де 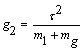 .
.
Якщо вантаж
![]() відсутній
(вільний нижній кінець нитки,
відсутній
(вільний нижній кінець нитки, ![]() ), тоді в (16) при
обчисленні коефіцієнта
), тоді в (16) при
обчисленні коефіцієнта ![]() виникає ситуація
ділення на нуль. Щоб уникнути цього «навантажимо» вільний кінець нитки масою,
що дорівнює, наприклад, половині маси відрізка нитки довжиною
виникає ситуація
ділення на нуль. Щоб уникнути цього «навантажимо» вільний кінець нитки масою,
що дорівнює, наприклад, половині маси відрізка нитки довжиною ![]() , тобто
, тобто ![]() (див. підпрограму CoefN).
(див. підпрограму CoefN).
Аналогічна ситуація виникає якщо ![]() (коефіцієнт
(коефіцієнт ![]() в формулі (14)).
Щоб обійти це ускладнення, можна перенести місце кріплення вантажу
в формулі (14)).
Щоб обійти це ускладнення, можна перенести місце кріплення вантажу ![]() до точки
до точки ![]() , де за
граничної умови 1-го роду на верхньому кінці нитки наявність або відсутність
вантажу
, де за
граничної умови 1-го роду на верхньому кінці нитки наявність або відсутність
вантажу ![]() не має
значення. Саме такий підхід реалізований в процедурі CoefN.
не має
значення. Саме такий підхід реалізований в процедурі CoefN.
Розглянутий алгоритм виконання кроку за часом для нитки з массами ![]() і
і ![]() носить назву
явної схеми. Він реалізований у вигляді підпрограми StepNit.
носить назву
явної схеми. Він реалізований у вигляді підпрограми StepNit.
Procedure
StepNit; {явна схема}
Var S:integer;
Y:Coefr;
Begin
For S:=1 to m-1 do
Y[S]:=2*Yt[S]-Yp[S]+Е*(Yt[S-1]-Yt[S+1])(*Hx/2+
(Gn(S)-S*Hx)*(Yt[S-1]-2*Yt[S]+Yt[S+1]))
+Gt*Fxt(S, t);Т:=t+Tau;
If (Sg>0) and
(Sg<m) then Y[Sg]:=2*Yt[Sg]-Yp[Sg]+Е*(R1*(Yt[Sg+1]-Yt[Sg]*R2*(Yt[Sg]-(Yt[Sg-1]))+Gg*Fg(t);
Y[0]:=Yv(t);
If Sg<m
Then
Y[m]:=(2*Yt[m]-Yp[m]+Е*Hx*Y[m-1]+G1*Fm(t))/(1+Е*Hx)
Else Y[m]:=(2*Yt[m]-Yp[m]+Е*Hx*Y[m-1]+G2*(Fm(t)
+Fg(t))/(1+Е*Hx);
Y[- 1]:=m; Yp:=Yt;
Yt:=Y
End;
Явна схема, що реалізується в процедурі StepNit,
є умовно стійкою. Умова стійкості має
вигляд -
![]() . (18)
. (18)
Розглянемо тепер, так звану, неявну схему:
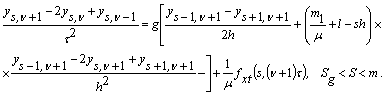 (19)
(19)
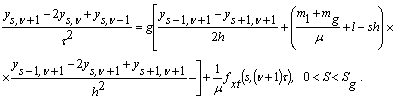 (20)
(20)
Вводячи на розгляд раніше згадувану функцію ![]() , зведемо співвідношення (19), (20) в одне і наведемо його у вигляді -
, зведемо співвідношення (19), (20) в одне і наведемо його у вигляді -
![]() (21)
(21)
де ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Система (21) доповнюється умовою ![]() , а також граничними умовами, після чого розв’язується методом прогонки
за схемою -
, а також граничними умовами, після чого розв’язується методом прогонки
за схемою -
![]() . (22)
. (22)
Щоб отримати рекурентні формули
для ![]() ,
,![]() , замінимо
, замінимо ![]() в (21) його
значенням із (22), а
в (21) його
значенням із (22), а ![]() на
на ![]() :
:
![]()
Останнє рівняння зводиться до вигляду -
![]() .
(23)
.
(23)
Зіставляючи (23) з (22), отримуємо
–
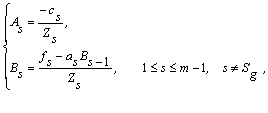 (24)
(24)
де ![]() .
.
Для точки ![]() у відповідності
до (3) в момент часу
у відповідності
до (3) в момент часу ![]() , маємо -
, маємо -
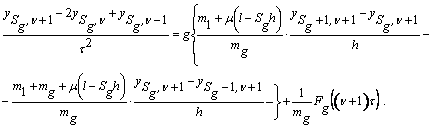
Помножимо останнє співвідношення на ![]() і замінимо
і замінимо ![]() його значенням із (22), перетворивши
його значенням із (22), перетворивши ![]() на
на ![]() . Отримуємо:
. Отримуємо:
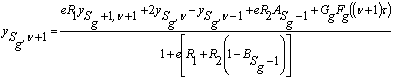 (25)
(25)
Зіставляючи (25) з (22), приходимо до висновку, що
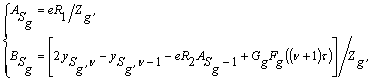 (26)
(26)
де ![]() .
.
Після того, як коефіцієнти ![]() ,
, ![]()
![]() визначені, можна
записати у відповідності з (22)
для
визначені, можна
записати у відповідності з (22)
для ![]() :
:
![]() . (27)
. (27)
Гранична умова для кінця нитки, коли
![]() , приводиться до вигляду
, приводиться до вигляду
![]() .
.
Перетворимо його:
![]() , (28)
, (28)
де ![]() ;
;![]() .
.
Якщо ж ![]() , тоді коефіцієнт
, тоді коефіцієнт
![]() в останньому виразі модифікується -
в останньому виразі модифікується -
![]() .
.
Коли порівняти праві частини (22)
і (23), то одержимо:
![]() . (29)
. (29)
Після визначення ![]() , виконання зворотного ходу за методом прогонки зводиться до реалізації залежності
(22) для
, виконання зворотного ходу за методом прогонки зводиться до реалізації залежності
(22) для
![]() , що змінюється
від
, що змінюється
від ![]() до 0 включно. Розглянутий алгоритм
реалізується в підпрограмі StepNitN.
до 0 включно. Розглянутий алгоритм
реалізується в підпрограмі StepNitN.
Procedure
StepNitN; {неявна схема}
Var Vs, As, Bs, Cs,
Fs, Zg:real;
S:integer;
А, В, Y:CooefR;
Begin
t:=t+Tau;
А[0]:=0; В[0]:=Yv(t);
For S:=1 to m-1 do
If S<>Sg Then Begin
Vs:=Gn(S)-S*Hx; As:=- Е*(Hx/2+Vs); Bs:=2*Е*Vs; Cs:=Е*(Hx/2-Vs);
Fs:=2*Yt[S]-Yp[S]+Gt*Fxt(S,
t); Zs:=As*А[S-1]+Bs;
А[S]:=- Cs/Zs; В[S]:=(Fs-As*В[S-1])/Zs
End
Else Begin
Zg:=1+Е*(R1+R2*(1-B[Sg-1])); А[Sg]:=Е*R1/Zg;
В[Sg]:=(2*Yt[Sg]-Yp[Sg]+Е*R2*А[Sg-1]+Gg
*Fg(t))/Zg
End;
If Sg<m Then E2:=(2*Yt[m]-Yp[m]+G1*Fm(t))/Е
Else
E2:=(2*Yt[m]-Yp[m]+G2*(Fm(t)+Fg(t))/Е;
Y[m]:=(В[m-1]+E2)/(E1-A[m-1]);
For S:=m-1 downto 0 do
Y[S]:=А[S]*Y[S+1]+В[S]; Y[-
1]:=m; Yp:=Yt; Yt:=Y
End;
Початковий стан нитки задається
масивами Yp (для ![]() ) і Yt (для
) і Yt (для ![]() ). Масив Yp формується відповідно до підпрограми-функції
Yn, а масив Yt - розкладанням в ряд Маклорена в околиці точки
). Масив Yp формується відповідно до підпрограми-функції
Yn, а масив Yt - розкладанням в ряд Маклорена в околиці точки ![]() , обмежуючись в ньому першими трьома доданками:
, обмежуючись в ньому першими трьома доданками:
![]() , (30)
, (30)
де ![]() і
і ![]() - відповідно
швидкість і прискорення точки нитки з координатою
- відповідно
швидкість і прискорення точки нитки з координатою ![]() для
для ![]() .
.
Значення ![]() визначимо з (30) для
визначимо з (30) для
![]() :
:
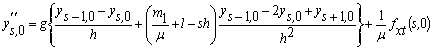
Підставляємо отриманий вираз
в (30):
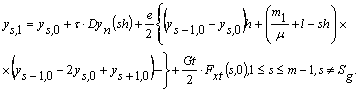 (31)
(31)
Значення ![]() визначається
граничною умовою (5) -
визначається
граничною умовою (5) -
![]() . (32)
. (32)
Значення ![]() обчислюється з (5) -
обчислюється з (5) -
![]() .
.
Приймаючи це до уваги, аналогічно (30) можна записати -
![]() . (33)
. (33)
Якщо ж
![]() , то враховуючи отримуємо -
, то враховуючи отримуємо -
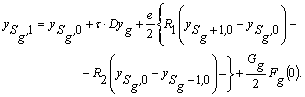 (34)
(34)
Якщо ж
![]() , то враховуючи
(5) будемо мати:
, то враховуючи
(5) будемо мати:
 (35)
(35)
Оформимо описаний алгоритм у вигляді підпрограми-процедури Init.
Procedure Init;
Var S:integer;
Begin
Т:=Tau;
For S:=0 to m do Yp[S]:=Yn(S*Hx);
For S:=1 to m-1 do
Yt[S]:=Yp[S]+Tau*Dyn(S*Hx)+Е/2*(Yp[S-1]-Yp[S])*Hx)*(Yp[S-1]-2*Yp[S]+Yp[S+1])
+Gt/2 *Fxt(S, 0); Yt[0]:=Yv(t);
If (Sg>0) and
(Sg<m) then
Yt[Sg]:=Yp[Sg]+Tau*Dyg+Е/2*(R1*(Yp[Sg+1]-Yp[Sg])(R2*(Yp[Sg]-Yp[Sg-1]))+Gg/2*
Fg(0);
If Sg< m then
Yt[m]:=Yp[m]+Tau*Dym+Е/2*(Yp[m-1]-Yp[m])+
G1*Fm(t);
If Sg=m then
Yt[m]:=Yp[m]+Tau*(m1*Dym+mg*Dyg)/(m1+mg)+Е/2*(Yp[m-1]-Yp[m])*Hx+G2*(Fm(t)+Fg(t))/2;
End;
Коефіцієнти, що використовуються в StepNit,
StepNitN, Init, обчислюються в
процедурі CoefN
Procedure CoefN;
Begin
С:=sqrt(g); Dt:=D/L;
Hx:=lng/m; Mu:=Pn1/g; Ks:=1;
Repeat
Tau:=Dt/ks; q:=С*Tau/Hx;
if q>0.5 then inc(ks)
until q<=0.5;
if Pg=0 then
begin Sg:=0;
Mg:=0 End
Else Begin
Sg:=round(Xg/Hx); Mg:=Pg/g End;
If Pm=0 then M1:=Mu*lng/(2*m)
Else M1:=Pm/g;
Е:=sqr(q); Tau2:=sqr(Tau); Gt:=Tau2/Mu;
If Sg>0 then begin R1:=(M1+Mu*(lng-Sg*Hx))*Hx/Mg;
Gg:=Tau2/Mg; R2:=R1+Hx
End;
G2:=Tau2/(M1+Mg); E1:=1+1/E;
G1:=Tau2/M1
End;