Математика/3. Теория вероятности и математической статистики
Юшковець Т.М.
Силенко В.Є., викл.
Донецький національний університет економіки і торгівлі
імені Михайла Туган-Барановського, Україна
Парадокси в математичній статистиці
Статистика — це
фізика чисел. П. Діаконіс
Спочатку статистика була "державною арифметикою". З давніх часів статистику використовували для того,
щоб інформувати правителей країн про величину податку,
який можна зібрати з їх підданих, або про кількість солдатів, на яку можна розраховувати у військовий час. У Китаї облік населення
проводився більше чотирьох тисяч років тому. Згідно Біблії, Мойсей також підраховував усіх чоловіків свого народу старших за 20 років. Їх виявилось 603 550 осіб.
Четверта книга Мойсейова (Числа) містить багато інших результатів підрахунку людей, однак вони здаються перебільшеними, так само як дані Афінея про кількість рабів у грецьких полісах часів Римської імперії. Дуже сумнівно, щоб у Афінах було 400 000 рабів, а у Коринфі — 460 000. Неясно, як були отримані ці дані, але точно відомо, що згідно результатів обліку населення Рим був першим містом з населенням
більше мільйона мешканців. Статистика стала наукою лише у XVII столітті. Її
засновниками є Джон Граунт (1620-1674
рр.) та сер Уїльям Петті (1623-1687 рр.). У книзі Граунта "Природні та політичні спостереження, зроблені над бюлетенями смертності" (1622 р.)
досліджувались питання народонаселення. У роботі Петті "Політична арифметика",
виданій у 1689 р. після смерті автора, Англія, Голландія та Франція порівнюються за їх населенням, торгівлею та судноплавством. Термін "політична
арифметика" можна вважати провісником слова "статистика". З розвитком капіталізму статистичними даними
почали цікавитись не лише державні
діячі, але й капіталісти. Для обробки даних використовувались все більш
складні математичні методи, при цьому зростала і користь від їх застосування,
наприклад, у страховій справі. Успіх у страховій справі визначається точністю
даних і належними математичними висновками. Математична статистика, поступово
розвиваючись з XVII ст., перетворилась в наш час на окрему область
математики. Її основною метою є отримання якомога вірнішої та кориснішої
інформації з даних результатів спостережень та вимірювань, або коротко, статистичної вибірки. Аналіз
текстів, проведений у 1913 р. Л.
Ейресом, уводить у оману або, принаймні, його легко неправильно
витлумачити. Ейрес стверджував, що 50 найбільш вживаних слів становлять
приблизно 50% звичайного тексту, 300 слів, які найчастіше зустрічаються,
становлять 75% тексту, а 1000 найбільш вживаних слів становлять 90%. Тим не
менш, не можна стверджувати, що якщо нам відомі 50 або 100 слів якоїсь мови, то
ми вже наполовину її розуміємо, бо знання кількох слів, навіть якщо вони часто
вживаються, навряд чи допоможе у розумінні будь-якого тексту. Не дивно, що
багато людей вважають, що існує три види брехні: безневинна брехня, нахабна
брехня та статистика. Сподіваємось, що пояснення парадоксів математичної
статистики допоможе нам добре розібратись у статистичних нісенітницях, бачити
користь та необхідність статистичних висновків, а також видобувати найбільш
важливу інформацію з даних.
Розглянемо, наприклад, парадокс Байєса. Томас Байєс є одним із видатних
засновників математичної статистики. Його теорема, доведена десь біля 1750 р. і
опублікована лише після його смерті, стала джерелом деяких суперечностей у
статистиці. Жар суперечок досі не
затих. Більше того, теоретичне провалля між послідовниками байєсівського та
антибайєсівського підходів продовжує збільшуватись. Просте формулювання теореми
Байєса полягає у наступному. Нехай А і В — випадкові події, що
мають ймовірності Р(А) > 0 і Р(В) > 0 відповідно. Позначимо через Р(АВ) ймовірність
сумісного здійснення подій А і
В, і нехай Р(А/В) — умовна
ймовірність А, якщо відомо, що В вже відбулась. Тоді ![]() , тобто
, тобто ![]() .
.
Отже, якщо В0,В1,... —
події, що попарно не перетинаються та мають додатні ймовірності, і одна з них
відбувається завжди (або принаймні з імовірністю 1), то ![]() .
.
Це і є формула Байєса. Вона показує, як за апріорними ймовірностями Р(Вк) (ймовірностям
подій Вк до того, як подія А відбулася) знайти апостеріорні ймовірності
(після того, як подія А відбулася). Якщо розглядати події Вк як
причини, то формула Байєса являє собою теорему про ймовірності причин. Сама по
собі теорема безсумнівна, але при більшості її використань ймовірності Р(Вк) невідомі. У
цьому випадку, як правило, вважають, що оскільки відсутня попередня інформація
про причини подій Вк,
то усі ймовірності Р(Вк) рівні, але
такий підхід, взагалі кажучи, неприйнятний. Байєс використовував свою теорему у
випадках, коли апріорні ймовірності були ймовірностями неперервних розподілів,
зокрема, рівномірного розподілу на інтервалі (0,1). За теоремою Байєса, якщо
при п + т спостереженнях подія, яка має невідому ймовірність р, відбулася
п разів, то ймовірність того, що р належить підінтервалу (а,b) інтервалу
(0,1), дорівнює 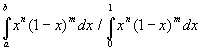 .
.
Байєс висунув ідею про те, що, якщо у нас немає жодної
попередньої інформації щодо р, то апріорна імовірнісна щільність
параметра р рівномірна на всьому інтервалі (0,1). Наприклад, якщо n = 1, m = 0, а = 1/2 і b = 1, то за наведеною вище формулою шанси того, що шукана
ймовірність р більша за 1/2, рівні 3/4. Досі лише деякі довіряють цьому
результату, зокрема тому, що вони сумніваються в рівномірності апріорного
розподілу.
Незнання апріорного розподілу виявилось настільки
руйнівним для обґрунтування статистичних висновків із теореми Байєса, що ця
теорема була майже виключена із статистичних досліджень. Але в другій третині XX сторіччя
байєсів підхід знову отримав деякий розвиток завдяки важливій ролі, яку він
грає під час пошуку допустимих і мінімаксних оцінок. Все більше поширювалась
думка про те, що послідовне застосування формули Байєса (коли після кожного
спостереження апостеріорні ймовірності перераховуються і на наступному кроці
вони використовуються як апріорні ймовірності) знижує роль початкового
апріорного розподілу, оскільки після багаторазового перерахунку початковий
розподіл навряд чи впливає на кінцевий апостеріорний розподіл.
Але існують деякі зауваження. Так, С. Бернштейн і Р. Мізес ще до 1920 р.
вказували на те, що при деяких умовах багаторазове застосування теореми Байєса
дає послідовність апостеріорних розподілів, які збігаються до істинного
розподілу, яким би не був апріорний розподіл. Тому апріорний розподіл
асимптотично ролі не грає. Як показує парадокс, таке твердження неможливе без
яких-яких обмежень.
Суб'єктивний вибір апріорних розподілів породжує загальне
питання про те, чи можливо взагалі об'єктивно визначати невідомі ймовірності та
ймовірнісні розподіли незалежно від наших спостережень і вимірів, чи вони мають смисл тільки
завдяки нашій суб'єктивній інформації. Індивідуальна або суб'єктивна
ймовірність відображає ступінь нашої впевненості в тому, що подія відбудеться.
Ми можемо говорити про суб'єктивну ймовірність, навіть якщо
"випадковість" не є об'єктивною. Однак необхідно підкреслити, що
значно більша частина вчених стверджує, що об'єктивна випадковість і об'єктивна
ймовірність існують. Вони впевнені у тому, що об'єктивні ймовірності майбутніх
подій закладені в сучасному стані світу. Так розумів об'єктивне існування
ймовірності лауреат Нобелівської премії Макс
Борн, відомий тим, що увів об'єктивну ймовірність у квантову
фізику.
Література:
1. Г.Секей. Парадоксы в теории вероятностей и математической
статистике: пер. с
англ. - Москва-Ижевск. Институт компьютерных исследований, 2003.
2. У світі математики. – 2008. – Т. 14,
Вип. 3