А.П.Мустафаев

Семипалатинский государственный университет имени Шакарима

Общие решения уравнения смешанного типа зависящее от конечного числа постоянных

Встречающиеся в приложениях в частных производных уравнений, как правило имеет целые семейство решений, причем в некоторых случаях можно указать способ их получения.

Если из постановки задачи известно, что искомая функция зависит только от одной линейной координаты то решение такой задачи сводится к интегрированию обыкновенного дифференциального уравнения. Общее решение такого уравнения содержит несколько произвольных постоянных, для определения которых надо использовать граничные условия и условия регулярности.

В этой работе покажем способ построения частного вида общего решения уравнения смешанного типа второго порядка вида

(1)

с использованием основных свойств характеристик, позволяющий сразу проинтегрировать уравнения. Для которого есть линия параболического выражения, где - натуральное число.

Нетрудно видеть что выражения

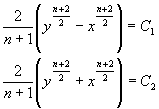, (2)

- суть характеристики уравнения (1) при и

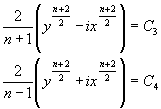, (3)

при

Тогда вводя вместо , новую переменную зависящее от характеристики

. (4)

Уравнения (1) приводится к дифференциальному уравнению вида

(5)

Решая полученные уравнения и переходя к старым переменным получим частный вид общего решения уравнения (1) зависящие от произвольных постоянных и .

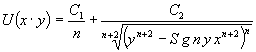(6)

На линии параболического выражения для найденного решения выполняются условия «склеивания»

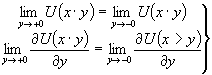. (7)

С другой стороны полученные решения позволяют легко найти частные виды общих решению уравнении при

, (8)

, (9)

при

(10)

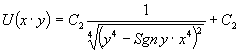(11)

и т.д.

Нетрудно проверить непосредственным дифференцированием что полученные выражения (6), (9), (11) действительно является решением соответственно уравнений (1), (8), и (10).

Литература:

1. М.М.Смирнов. Уравнения смешанного типа. – М:, «Наука» 1970 г. 295 с.

2. А.Б. Бицадзе. Некоторые классы уравнения в частных производных. – М:, «Наука» 1981 г. 448 с.

3. А.П.Мустафаев. Об одном методе нахождения элементарного решения уравнения Трикоми. «Современный научный вестник» №30 2008, 32-35 стр. Серия технические науки, математика, информатика. г. Белград (Россия).