Технические науки/2. Механика
Бакиров М.Ж.,
Михайлов В.Ф.
Карагандинский
государственный технический университет, Казахстан
Стохастическая устойчивость нестационарных
параметрических систем
Малые поперечные колебания механических
систем, возбуждаемых периодической параметрической нагрузкой описываются
уравнением Матье-Хилла. Если амплитуда нагрузки представляет собой случайный процесс,
то это уравнение для широкого класса задач может быть записано в виде уравнения
с периодическим, случайным и периодически модулированным случайным
параметрическим воздействием:
где 
, 
, 
– коэффициенты
детерминированного периодического, случайного аддитивного и мультипликативного
параметрического возбуждения; 
– функция,
описывающая изменение во времени обобщенного перемещения; 
– коэффициент
затухания; 
, 
– частота собственных
колебанийи частота внешнего воздействия; 
– центрированный
стационарный случайный процесс, который представим спектральным разложением
Решение уравнения можно представить в виде
,где 
, 
– детерминированные
функции времени и частоты. Случайные спектры 
и 
удовлетворяют соотношению Винера-Хинчина
,
– спектральная
плотность нагрузки; 
– дельта-функция
Дирака.
Подставим
и в и осредним с учетом :
, где 
– взаимная спектральная
плотность перемещения и нагрузки;
; 
.
Подставляя
вновь и в и применяя операцию свертывания, получаем
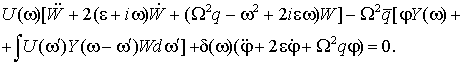
Умножим полученное уравнение на комплексно-сопряженный
спектр 
и произведем
осреднение в предположении гауссовости случайных процессов. После
интегрирования по частоте получим уравнение движения в среднеквадратичном,
которое определяет связь между спектрами.
. Уравнение
представляет собой линейное дифференциальное уравнение
с периодическими коэффициентами. Согласно теореме Хаупта [1] на границе
перехода из устойчивых в неустойчивые положения и наоборот, фундаментальные
решения должны быть периодическими. На основании вышеизложенного, вблизи границ
главной области неустойчивости детерминированные функции 
и 
можно представить так
, 
. Подставив
в уравнение и отбрасывая члены с утроенной частотой, получаем
систему из двух уравнений
,
,
где 
, 
, 
.
Из этой
системы находим
,
,где
.
Подставим
далее в уравнение и получим
Учитывая
выражение и обозначив
приходим к следующей системе:
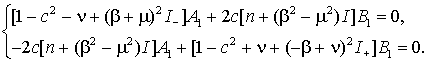
Приравнивая
определитель системы к нулю, получим границы главной области неустойчивости:
где
; 
.
Если
случайное возбуждение отсутствует, то 
и получаем известное
детерминированное решение [1]
.
Если затухание очень мало (
), то 
и
– правая ветвь;
При
известной спектральной плотности нагрузки 
интегралы можно вычислить в явном виде, используя теорему о
вычетах. Найдем корни 
, 
,
где 
, 
.
Легко показать, что 
и 
полюсы первого
порядка, находящиеся в верхней полуплоскости. Значения остальных двух корней
зависят от величины параметра 
.
При
, 
, 
– являются полюсами
первого порядка, лежащими в верхней полуплоскости. Здесь
.
При 
, 
– полюсы второго порядка, лежащие в верхней полуплоскости.
При
, 
являются полюсами
первого порядка. Причем 
находится всегда в
верхней полуплоскости, а 
будет находиться в
верхней полуплоскости при 
.
Пусть
внешняя нагрузка представляет собой экспоненциально-коррелированный процесс со
спектральной плотностью
,
где 
– дисперсия процесса 
, 
– параметр
широкополосности.
Вводя безразмерный параметр 
, преобразуем интегралы к виду
, 
,
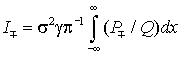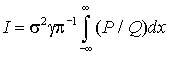где 
, 
, 
.
Теперь
к имеющимся особым точкам добавляются 
, 
.
Согласно теореме о вычетах
,где
– вычет функции в особых точках, лежащих в нижней полуплоскости.
Если в окрестностях полюса первого порядка 
, причем 
, то
При 
в нижней
полуплоскости имеем только один полюс 
. Тогда
, 
,где
,
.
При
надо рассмотреть три
случая:
1. 
; значения интегралов определяются выражениями
2. 
; в этом случае в нижней полуплоскости будут два корня 
. Используя формулы , , находим
,
3. 
, в этом случае 
и по теореме о
вычетах
.
Отсюда следует
,
.
После вычисления интегралов границы
главной области определяются из уравнения . Для решения этого уравнения используется один из приближенных
методов решения алгебраических уравнений.
Анализ уравнения показывает наличие некоторого порогового значения
коэффициента возбуждения 
. При 
потери устойчивости
не происходит. Пороговое значение 
определяется из
условия равенства нулю подкоренного выражения в уравнении
.
Этому значению соответствует пороговая частота
.
Решая совместно последние два равенства, определяем
пороговые значения коэффициента возбуждения и соответствующую ему частоту.
Решение этой системы можно провести методом последовательных приближений. Составлена
программа определения границ главной области неустойчивости. Результаты
расчетов для экспоненциально-коррелированного процесса (
, 
) при 
, 
, 
показаны на рисунке
1.
Рис.1 Главная область неустойчивости при
экспоненциально-коррелированном воздействии
Литература:
1. Стокер Дж. Нелинейные колебания в механических и
электрических системах. – М.: Изд. иностранной лит-ры, 1953. – 256 с.