Бельков Д.В.

Донецкий национальный технический университет

Метод оптимального распределения файлов в компьютерной сети

В данной работе решается задача уменьшения времени отклика компьютерной сети за счет оптимизации размещения файлов распределенной системы. Для решения задачи предлагается алгоритм, относящийся к классу алгоритмов муравьиной колонии. Этот класс алгоритмов появился в результате исследований поведения живых муравьев. Муравей, двигаясь по определенному маршруту, оставляет за собой след пахнущего вещества (феромона). Такое вещество влияет на выбор маршрута: выбирается то направление движения, где уровень феромона больше. Самоорганизация муравьев обеспечивается взаимодействием следующих компонентов: случайность, многократность, положительная обратная связь, отрицательная обратная связь. Центральной идеей муравьиного алгоритма является накопление и использование статистических данных, собираемых искусственными муравьями.

Обозначим: - количество запросов к файлу i из узла j в единицу времени; , если файл i расположен в узле j, иначе ; - объем файла i; - объем узла j, i=1...m, j=1…n.

В задаче (1)-(3) необходимо найти матрицу размещений файлов X. В задаче максимизируется суммарный поток локальных запросов. Задача размещения файлов по узлам компьютерной сети имеет вид:

Целевая функция

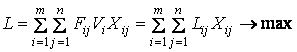(1)

Ограничения:

,, i=1...m (2)

(3)

Для решения задачи (1)-(3) в данной работе предлагается следующий алгоритм:

Присвоить переменной record первоначальное (небольшое) значение;

Присвоить переменной t значение 1;

While Do

Begin

For i:=1 to m do

Begin

Сформировать вектор P(n) вероятностей размещения i-го файла в j-й узел.

Сгенерировать случайную величину g, распределенную по закону P(n);

Если и условие (3) выполняется, то назначить i-й файл в j-й

узел, иначе - сгенерировать новое значение случайной величины g.

End;

Вычислить значение целевой функции по формуле (1) и присвоить его

переменной c_f;

If c_f > record then

Begin

Присвоить переменной record значение переменной c_f и сохранить

рекордное решение;

End;

Присвоить переменной t значение t+1;

End;

Вывести наилучшее решение и завершить алгоритм.

Пусть - количество феромона, накопленное очередным муравьем на маршруте j, – коэффициент испарения феромона, , – первоначальный уровень феромона, , - уровень феромона на маршруте j. Вероятность размещения файла в узел j вычисляется по формуле:

(4)

При выборе узла p для размещения файла происходит увеличение значения : , значение переменной d должно быть одного порядка с оптимальным значением целевой функции. При переходе к очередной итерации алгоритма уровень феромона накапливается: .

Для исследования работы муравьиного алгоритма проведен вычислительный эксперимент. Предложенным алгоритмом и методом полного перебора решена задача распределения m файлов среди n узлов сети, m=8, n=3. Объемы файлов - случайные числа, распределенные по закону Парето. Программа составлена в среде Delphi. Для полного перебора требуется итераций, муравьиным алгоритмом выполнено 1000 итераций. Оптимальное значение целевой функции (ЦФ), полученное полным перебором, равно 3332,18. Это значение найдено муравьиным алгоритмом на 298 и 504 итерациях. Динамика поиска решений показана на рисунке 1.

Рисунок 1. – Поиск оптимальных решений