Математика / 5. Математичне моделювання

Камаєва С.О.

Івано-Франківський національний технічний університет нафти і газу, Україна

Відновлення температурного поля пластини неопуклої форми

Задача відновлення функції на досліджуваній області завжди привертала увагу спеціалістів, як теоретиків, так і прикладників. Для простих областей цю задачу вдається розв’язати аналітично, а для областей складної конфігурації без залучення чисельних методів не обійтись. Так, з появою методу скінченних елементів (МСЕ) з’явилась можливість відновлення функції декількох аргументів, використовуючи при цьому трикутні та чотирикутні скінченні елементи [1, 2]. З розвитком МСЕ набули широкої популярності його спрощені схеми, які ґрунтуються на геометричних уявленнях [3, 4].

Ціллю даної роботи є побудова стаціонарного поля (наприклад, температурного) на пластині неопуклої форми (рис. 1) при заданих постійних температурах в граничних вузлах (табл. 1).

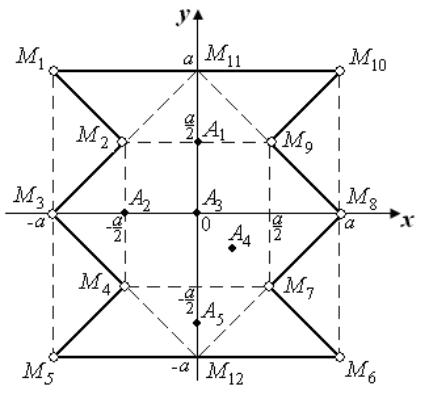
Рис. 1 Пластина неопуклої форми

Таблиця 1

Значення температури в граничних точках , [^oC]

	1	2	3	4	5	6	7	8	9	10
	10	45	55	80	90	100	70	60	35	20

При цьому вважаємо, що розподіл температур вздовж границі пластини відбувається за лінійним законом. Отже,

Задача полягає у визначенні температури в довільно вибраній точці заданої області. Для розв’язання даної задачі введемо у розгляд скінченні елементи, вершини яких розміщені в граничних вузлах. Ці елементи вибираємо так, щоб лінійна комбінація їх мір відповідала мірі досліджуваної області (в даному випадку мірою буде площа). В кожному з цих елементів для знаходження температури в довільно взятій точці застосуємо формулу:

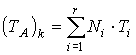, (1)

де – температура у внутрішній точці -го СЕ,

– значення температури в граничних точках, які є вершинами скінченного елемента (, де – кількість вершин СЕ ),

– базисні функції.

Після цього виконаємо зважене усереднення отриманих температурних значень, враховуючи вплив скінченних елементів на досліджувану точку. За приведеною схемою побудовано декілька математичних моделей.

Модель 1. З метою врахування всієї граничної інформації розглянемо білінійний () та біквадратичний () серендипові скінченні елементи. Неважко бачити, що площі цих елементів відповідно дорівнюють: , , а площа пластини .

Тоді має місце таке співвідношення: .

Далі переносимо вагові коефіцієнти на значення температури, отримані у відповідних скінченних елементах, з метою уточнення температури в досліджуваній точці. Нагадаємо, що при перенесенні вагових коефіцієнтів враховується вплив кожного зі скінченних елементів на дану точку. Отже,

,

де та знайдені згідно (1) з використанням класичних базисів [1].

Модель 2. Введемо в розгляд такі скінченні елементи: біквадратичний () та білінійний (). Їхні площі відповідно дорівнюють: , .

Має місце таке співвідношення: .

Тоді:

.

Зазначимо, що в алгоритмі побудови базисних функцій на біквадратичному елементі враховано поворот системи координат на кут .

Модель 3. Тепер розглянемо три білінійні елементи: , та , площі яких відповідно рівні:

, , .

Має місце співвідношення: .

А для температур маємо:

.

З метою підтвердження достовірності отриманих результатів цю задачу було розв’язано за допомогою МСР. При цьому досліджувана область покривалася сіткою з квадратними комірками , в результаті чого складено систему з 65 лінійних рівнянь і розв’язано в програмному середовищі MathCad. Результати розрахунків в контрольних точках (рис. 1) за МСР та побудованими моделями наведені в табл. 2 ( – відносна похибка в порівнянні з МСР, [%]).

Таблиця 2

Результати розрахунків в контрольних точках, [^оС]

	МСР	Модель 1	Модель 2	Модель 3
	38.643	38.958, =0.815	37.344, =3.362	38.125, =1.340
	58.928	60.417, =2.527	57.188, =2.953	59.018, =0.153
	57.372	57.500, =0.223	56.875, =0.866	56.786, =1.021
	65.237	65.169, =0.104	65.469, =0.356	65.000, =0.363
	85.316	84.531, =0.920	85.000, =0.370	84.442, =1.024

Як видно з табл. 2, результати, отримані для моделей 1-3, мало відрізняються від результатів, отриманих за МСР. В той же час описаний спосіб, будучи безсітковим, не потребує складання і розв’язування систем рівнянь, що дозволяє суттєво зменшити об’єм роботи при задовільній точності обчислень.

ЛІТЕРАТУРА:

1. Зенкевич О., Морган К. Конечные элементы и аппроксимация. – М.: Мир, 1986. – 328 с.

2. Стренг Г., Фикс Дж. Теория метода конечных элементов. – М.: Мир, 1977. – 349 с.

3. Хомченко А.Н., Камаева Л.И. Геометрические аспекты серендиповых аппроксимаций. Ивано-Франк. ин-т нефти и газа.– Ивано-Франковск, 1987.– 10 с.– Деп. в УкрНИИНТИ 27.03.87, № 1062.

4. Хомченко А.Н., Камаева Л.И. Способ вращения симплекс-элемента в строительной механике // Неделя науки, техники и передового опыта. Совершенствование методов расчета и проектирования современных видов строительных конструкций: Тез. докл. Респ. научно-практ. конф. 21-25 ноября 1988. – Ровно, 1988. – С. 154-155.