Аспирант Набродов П.А.

Ставропольский государственный университет, Россия

Синтез дискретного согласованного фильтра сигналов в нейросетевом базисе

Существующие дискретные согласованные фильтры сигналов (рисунок 1) имеют ряд недостатков. Это низкая помехоустойчивость, обусловленная отсутствием учета влияния постоянных искажений сигналов, вызванных внешними аддитивными и мультипликативными помехами. Дискретные согласованные фильтры сигналов существенно теряют в помехоустойчивости при возникновении несократимых ошибок в сигнале, так как их перемножители отражают импульсные характеристики ожидаемого сигнала и фиксированы, и в случае искажения принимаемого сигнала отклик таких фильтров существенно снижается [2].

Рисунок 1 − Согласованный фильтр

Согласованный фильтр решает задачу вычисления автокорреляционной функции принимаемого сигнала и импульсной характеристики ожидаемого сигнала в зависимости от сдвига согласно выражения

, (1)

где – разрядность сигнала и, соответственно, фильтра [2].

Максимум определяется в момент обнаружения сигнала. Очевидно, что искажения принимаемого сигнала могут существенно снизить корреляционный отклик . Структура согласованного фильтра соответствует схеме обученного нейрона, реализующего функцию

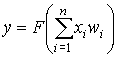, (2)

где − функция активации, − входной вектор нейрона, − вектор весовых коэффициентов [2].

Если обратить внимание на структуру согласованного фильтра (рисунок 1), то можно заметить, что она соответствует схеме обученного нейрона [3]. Следовательно, повысить помехоустойчивость дискретного согласованного фильтра возможно за счет введения в его структуру блока ассоциативной памяти в виде нейронной сети (НС) (рисунок 2).

Рисунок 2 − Адаптированный согласованный фильтр

Для моделирования работы фильтра выберем схему обучения НС по Хэббу [1, 4]. Такая схема позволяет контролировать помехоустойчивость системы, основную характеристику систем телекоммуникаций.

Выберем начальные весовые коэффициенты случайным образом по нормальному закону с математическим ожиданием и дисперсией .

В результате получим математическую модель СФ с интегрированной в него НС в виде

, (3)

где – значение веса от входа к нейрону .

Произведем обучение предложенной нейронной сети для различных четырех битных сигналов , , и .

На рисунке 3 графики зависимости среднеквадратического отклонения (СКО) результата обучения от числа тактов обучения при различных скоростях обучения.

Рисунок 3 − Зависимость среднеквадратического отклонения от числа тактов обучения для различных скоростей обучения

Очевидно, что значение порогов зависит от скорости обучения, начальных значений весовых коэффициентов НС, активационной функции, о чем свидетельствует рисунок 3.

Необходимо дальнейшее исследование аналогичных телекоммуникационных устройств с целью определения эффективности внедрения НС.

Литература:

1. Червяков, Н.И. Модулярные параллельные вычислительные структуры нейропроцессорных систем [Текст] / Червяков Н.И. и др. – Москва: Изд-во Физматлит, 2003.

2. Смирнов, А.А. Принципы построения инфокоммуникационных систем для обработки и передачи параллельных данных [Текст] / Смирнов А.А., Чемерисов А.Ю., Набродов П.А – Ставрополь: Изд-во Альфа Принт, 2009. – 172 с.

3. Смирнов А.А., Сахнюк П.А., Сенник В.В. Синтез схем цифровой обработки сигналов на основе обучения нейросетевых схем // Нейрокомпьютеры: разработка, применение, 2004, № 5 – 6, с. 91 – 93.

4. Комашинский, В.И. Нейронные сети и их применение в системах управления и связи [Текст] / Комашинский В.И., Смирнов Д. А. – Москва: Изд-во Горячая линия-Телеком, 2002.