Современные информационные
технологии / 4. Информационная безопасность
Коваленко М.П.
МОУ «Институт инженерной физики», Россия
Смирнов Я.Д.
МОУ «Институт инженерной физики», Россия
Использование искусственных
нейронных сетей при внедрении цифровых водяных знаков в графические изображения
Введение
Стеганографические алгоритмы, производящие встраивание скрываемой информации в частотную область изображений, получили широкое распространение в силу некоторых выгодных отличий от остальных стеганографических алгоритмов. К сильным сторонам данного вида алгоритмов, прежде всего, следует отнести возможность встраивать информацию в изображения-контейнеры, сжатые форматом JPEG, который является одним из наиболее распространенных форматов хранения и передачи мультимедиаконтента на сегодняшний день. Также к преимуществам данного вида алгоритмов можно отнести и достаточно хорошую устойчивость к различного рода внешним воздействиям или атакам на изображение-контейнер.
Использование дискретно-косинусного
преобразования
в стеганографии
В основе большинства стеганографических алгоритмов частотной области лежит дискретно-косинусное преобразование (ДКП). Такие алгоритмы предварительно разбивают исходное изображение-контейнер на блоки, как правило, размером 8×8 пикселей, в дальнейшем подвергающиеся ДКП, результатом которого является матрица коэффициентов, представленная на рисунке 1.
Рисунок 1 – Матрица ДКП коэффициентов
, (1)
и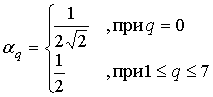 
, (2-3)
где 0 £ p £ 7; 0 £ q £ 7; A – матрица, подвергаемая ДКП; B – матрица ДКП коэффициентов.
В ДКП матрице, вычисляемой для блоков размером 8×8
пикселей по формулам 1-3, коэффициенты низкочастотных компонент располагаются
ближе к верхнему левому углу, в то время как коэффициенты высокочастотных
компонент сгруппированы в правой нижней части матрицы. Низкочастотные
коэффициенты содержат преобладающую часть энергии изображения, в то время как
высокочастотные компоненты наиболее уязвимы для внешних воздействий [1]. Поэтому
авторы большинства алгоритмов считают пригодными для встраивания только
среднечастотные коэффициенты. Так, например, согласно алгоритму, разработанному
E. Koch и J. Zhao [2],
внедрение бита 
в псевдослучайно
отобранные коэффициенты 
и 
ДКП блока изображения
под номером 
осуществляется по
следующему правилу:
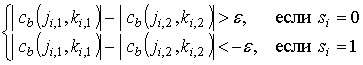, (4)
где 
– некоторая
положительная величина, влияющая на степень стойкости внедрения. Но ведь для
каждого ДКП блока способов изменения его коэффициентов, удовлетворяющих
соотношению (4), существует целое множество. Как же выбрать наиболее
подходящее? Очевидно, что данный выбор должен осуществляться с учетом оценки
вносимых изменениями ДКП коэффициентов искажений изображения. Но как произвести
эту оценку? Одним из способов решения данной проблемы является использование
искусственных нейронных сетей.
Использование искусственных нейронных сетей
при внедрении цифровых водяных знаков в графические изображения
Как уже ранее упоминалось, преобладающая часть энергии изображения содержится в низкочастотных коэффициентах. Предположим, что среднечастотные коэффициенты, расположенные в пределах одной диагонали ДКП матрицы, связаны некоторой нелинейной функциональной зависимостью со всеми коэффициентами, расположенными на предыдущих диагоналях. Тогда для каждой такой диагонали можно создать искусственную нейронную сеть, аппроксимирующую данную функциональную зависимость.
Согласно [3] искусственные нейронные сети прямого распространения являются универсальным средством аппроксимации функций. При этом наиболее часто использующейся в настоящее время разновидностью нейронных сетей данного класса является многослойный персептрон [4].
Многослойный персептрон в общем представлении состоит из следующих элементов:
- множества входных узлов, которые образуют входной слой;
- одного или нескольких скрытых слоев вычислительных нейронов;
- одного выходного слоя нейронов.
На рисунке 2 [5] изображена структура двухслойного персептрона.
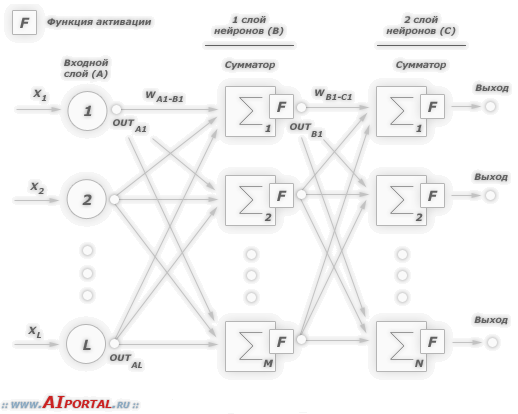
Рисунок 2 – Пример двухслойного персептрона
Согласно [6] многослойная нейронная сеть может моделировать функцию практически любой степени сложности. Теоретическое обоснование данного утверждения базируется на теореме А.Н. Колмогорова, доказавшего, что любую непрерывную функцию n переменных можно представить в виде суперпозиции одноместных функций и операции сложения [7, 8].
Позднее Р. Хехт-Нильсен доказал представимость непрерывной функции многих переменных с помощью двухслойной нейронной сети с n компонентами входного сигнала, 2∙n + 1 компонентами первого (скрытого) слоя с сигмоидными функциями активации и m компонентами второго слоя с неизвестными функциями активации [9]. Исходя из этого, в рамках решаемой задачи нейронные сети будут иметь размеры, представленные в таблице 1.
Таблица 1 – Размеры слоев ИНС
|
Номер диагонали |
Размер слоя |
||
|
Входного |
Скрытого |
Выходного |
|
|
7 |
21 |
43 |
7 |
|
8 |
28 |
57 |
8 |
|
9 |
36 |
73 |
7 |
|
10 |
43 |
87 |
6 |
В качестве функции активации нейронов выходных слоев также возьмем сигмоиду, как наиболее часто применяемую в практических задачах [10].
Сигмоидальная функция активации – монотонно возрастающая
всюду дифференцируемая 
-образная нелинейная функция с насыщением.
Примером сигмоидальной функции является гиперболический тангенс:
, (5)
где 
– это параметр,
влияющий на наклон сигмоидальной функции. Остается только для каждого слоя
каждого из рассматриваемых многослойных персептронов определить значение данного
параметра. Для этого выполним предварительное обучение всех сетей по алгоритму RPROP
[11] втечение 1000 циклов на 524288 примерах обучающей выборки (сформирована на
основе взятых с Интернет-хранилища imagesbase.com изображений разной тематики).
При чем для того, чтобы снизить влияние псевдослучайной инициализации весов,
для каждой диагонали ДКП матрицы сгенерируем и обучим 5 сетей. Полученные
результаты обучения представлены в таблице 2.
Таблица 2 – Результаты предварительного обучения
|
№ диаг. |
Параметр |
Значение функции ошибок |
|||||||
|
Скр. слой |
Вых. слой |
1 |
2 |
3 |
4 |
5 |
Ср. знач |
СКО |
|
|
7 |
0.01 |
0.01 |
19.16 |
19.61 |
19.27 |
19.39 |
19.37 |
19.36 |
0.17 |
|
7 |
0.01 |
0.25 |
20.05 |
20.06 |
19.99 |
20.02 |
20.03 |
20.03 |
0.03 |
|
7 |
0.01 |
1.00 |
20.04 |
20.04 |
20.04 |
20.07 |
20.06 |
20.05 |
0.02 |
|
7 |
0.01 |
5.00 |
20.07 |
20.07 |
20.05 |
20.05 |
20.09 |
20.07 |
0.02 |
|
7 |
0.25 |
0.01 |
18.86 |
18.84 |
18.86 |
18.90 |
18.93 |
18.88 |
0.03 |
|
7 |
0.25 |
0.25 |
19.52 |
19.55 |
19.61 |
19.60 |
19.69 |
19.60 |
0.06 |
|
7 |
0.25 |
1.00 |
20.14 |
20.07 |
20.09 |
20.03 |
20.13 |
20.09 |
0.04 |
|
7 |
0.25 |
5.00 |
21.01 |
20.88 |
20.58 |
20.64 |
20.49 |
20.72 |
0.22 |
|
7 |
1.00 |
0.01 |
18.83 |
18.94 |
18.92 |
18.97 |
19.00 |
18.93 |
0.06 |
|
7 |
1.00 |
0.25 |
19.56 |
19.50 |
19.46 |
19.58 |
19.62 |
19.54 |
0.07 |
|
7 |
1.00 |
1.00 |
20.16 |
20.01 |
20.19 |
20.14 |
20.16 |
20.13 |
0.07 |
|
7 |
1.00 |
5.00 |
21.25 |
22.68 |
20.97 |
20.93 |
20.66 |
21.30 |
0.80 |
|
7 |
5.00 |
0.01 |
19.25 |
19.17 |
19.31 |
19.20 |
19.29 |
19.24 |
0.06 |
|
7 |
5.00 |
0.25 |
19.96 |
19.79 |
19.97 |
19.95 |
19.83 |
19.90 |
0.08 |
|
7 |
5.00 |
1.00 |
21.87 |
21.40 |
20.98 |
21.25 |
20.85 |
21.27 |
0.40 |
|
7 |
5.00 |
5.00 |
27.60 |
27.14 |
26.99 |
33.63 |
28.70 |
28.81 |
2.77 |
|
8 |
0.01 |
0.01 |
14.89 |
14.92 |
14.89 |
14.86 |
14.83 |
14.88 |
0.03 |
|
8 |
0.01 |
0.25 |
15.23 |
15.23 |
15.18 |
15.19 |
15.21 |
15.21 |
0.03 |
|
8 |
0.01 |
1.00 |
15.33 |
15.31 |
15.39 |
15.38 |
15.32 |
15.35 |
0.03 |
|
8 |
0.01 |
5.00 |
15.37 |
15.37 |
15.34 |
15.34 |
15.36 |
15.35 |
0.01 |
|
8 |
0.25 |
0.01 |
14.49 |
14.56 |
14.58 |
14.52 |
14.54 |
14.54 |
0.04 |
|
8 |
0.25 |
0.25 |
15.10 |
15.07 |
15.16 |
15.11 |
15.11 |
15.11 |
0.03 |
|
8 |
0.25 |
1.00 |
15.47 |
15.44 |
15.42 |
15.45 |
15.43 |
15.44 |
0.02 |
|
8 |
0.25 |
5.00 |
16.13 |
16.08 |
16.16 |
16.58 |
16.10 |
16.21 |
0.21 |
|
8 |
1.00 |
0.01 |
14.61 |
14.67 |
14.62 |
14.60 |
14.67 |
14.63 |
0.03 |
|
8 |
1.00 |
0.25 |
15.14 |
15.19 |
15.19 |
15.22 |
15.19 |
15.19 |
0.03 |
|
8 |
1.00 |
1.00 |
15.49 |
15.70 |
15.51 |
15.42 |
15.41 |
15.51 |
0.12 |
|
8 |
1.00 |
5.00 |
16.98 |
16.55 |
17.80 |
17.20 |
17.73 |
17.25 |
0.53 |
|
8 |
5.00 |
0.01 |
14.87 |
14.86 |
14.86 |
14.86 |
14.85 |
14.86 |
0.01 |
|
8 |
5.00 |
0.25 |
15.34 |
15.29 |
15.43 |
15.37 |
15.39 |
15.36 |
0.05 |
|
8 |
5.00 |
1.00 |
16.34 |
16.53 |
17.24 |
16.63 |
16.46 |
16.64 |
0.35 |
|
8 |
5.00 |
5.00 |
30.22 |
29.56 |
26.14 |
25.16 |
26.69 |
27.55 |
2.22 |
|
9 |
0.01 |
0.01 |
10.08 |
10.09 |
10.07 |
10.07 |
10.07 |
10.08 |
0.01 |
|
9 |
0.01 |
0.25 |
10.27 |
10.26 |
10.25 |
10.30 |
10.26 |
10.27 |
0.02 |
|
9 |
0.01 |
1.00 |
10.39 |
10.34 |
10.35 |
10.34 |
10.34 |
10.35 |
0.02 |
|
9 |
0.01 |
5.00 |
10.38 |
10.40 |
10.41 |
10.40 |
10.39 |
10.40 |
0.01 |
|
9 |
0.25 |
0.01 |
10.05 |
10.07 |
10.05 |
10.04 |
10.07 |
10.06 |
0.01 |
|
9 |
0.25 |
0.25 |
10.36 |
10.39 |
10.40 |
10.35 |
10.38 |
10.38 |
0.02 |
|
9 |
0.25 |
1.00 |
10.43 |
10.45 |
10.45 |
10.43 |
10.45 |
10.44 |
0.01 |
|
9 |
0.25 |
5.00 |
10.95 |
11.11 |
11.17 |
10.82 |
10.87 |
10.98 |
0.15 |
|
9 |
1.00 |
0.01 |
10.08 |
10.08 |
10.08 |
10.08 |
10.10 |
10.08 |
0.01 |
|
9 |
1.00 |
0.25 |
10.37 |
10.36 |
10.37 |
10.37 |
10.41 |
10.37 |
0.02 |
|
9 |
1.00 |
1.00 |
10.64 |
10.48 |
10.57 |
10.53 |
10.55 |
10.56 |
0.06 |
|
9 |
1.00 |
5.00 |
12.54 |
11.78 |
12.11 |
11.72 |
11.60 |
11.95 |
0.38 |
|
9 |
5.00 |
0.01 |
10.15 |
10.13 |
10.13 |
10.13 |
10.13 |
10.13 |
0.01 |
|
9 |
5.00 |
0.25 |
10.54 |
10.58 |
10.49 |
10.41 |
10.65 |
10.54 |
0.09 |
|
9 |
5.00 |
1.00 |
11.78 |
11.75 |
11.68 |
12.14 |
11.21 |
11.71 |
0.33 |
|
9 |
5.00 |
5.00 |
22.58 |
21.59 |
20.15 |
20.39 |
22.29 |
21.40 |
1.10 |
|
10 |
0.01 |
0.01 |
6.72 |
6.73 |
6.72 |
6.72 |
6.71 |
6.72 |
0.01 |
|
10 |
0.01 |
0.25 |
6.93 |
6.89 |
6.93 |
6.92 |
6.86 |
6.91 |
0.03 |
|
10 |
0.01 |
1.00 |
6.93 |
6.98 |
6.99 |
6.99 |
6.96 |
6.97 |
0.03 |
|
10 |
0.01 |
5.00 |
7.00 |
6.99 |
7.00 |
6.98 |
6.99 |
6.99 |
0.01 |
|
10 |
0.25 |
0.01 |
6.72 |
6.71 |
6.73 |
6.72 |
6.72 |
6.72 |
0.01 |
|
10 |
0.25 |
0.25 |
6.96 |
6.99 |
6.95 |
6.93 |
6.97 |
6.96 |
0.02 |
|
10 |
0.25 |
1.00 |
7.04 |
7.02 |
7.02 |
7.03 |
7.02 |
7.02 |
0.01 |
|
10 |
0.25 |
5.00 |
7.33 |
7.34 |
7.39 |
7.53 |
7.51 |
7.42 |
0.09 |
|
10 |
1.00 |
0.01 |
6.74 |
6.73 |
6.73 |
6.72 |
6.72 |
6.73 |
0.01 |
|
10 |
1.00 |
0.25 |
6.99 |
6.99 |
6.98 |
7.00 |
7.00 |
6.99 |
0.01 |
|
10 |
1.00 |
1.00 |
7.09 |
7.18 |
7.14 |
7.20 |
7.28 |
7.18 |
0.07 |
|
10 |
1.00 |
5.00 |
8.32 |
8.63 |
8.47 |
8.54 |
8.60 |
8.51 |
0.12 |
|
10 |
5.00 |
0.01 |
6.77 |
6.78 |
6.81 |
6.80 |
6.79 |
6.79 |
0.01 |
|
10 |
5.00 |
0.25 |
7.08 |
7.05 |
7.14 |
7.01 |
7.10 |
7.07 |
0.05 |
|
10 |
5.00 |
1.00 |
8.03 |
7.91 |
8.54 |
8.76 |
8.27 |
8.30 |
0.35 |
|
10 |
5.00 |
5.00 |
18.42 |
16.19 |
17.23 |
15.58 |
14.89 |
16.46 |
1.39 |
На основании представленных в таблице 2 данных можно сделать следующие выводы:
1) с увеличением значения параметра наклона функции активации для нейронов скрытого и выходного слоев растет влияние на результат обучения начальных значений весов (результата инициализации сети);
2) для каждой из рассматриваемых диагоналей ДКП матрицы значение параметра наклона функции активации нейронов скрытого слоя соответствующей сети, обеспечивающее минимальное значение функции ошибок, различно.
Кроме того, согласно все тем же данным, для каждой из рассматриваемых диагоналей ДКП матрицы значение параметра наклона функции активации нейронов выходного слоя соответствующей сети, обеспечивающее минимальное значение функции ошибок, одинаково и равно 0.01. Поскольку это минимальное значение параметра из числа рассмотренных, необходима дополнительная проверка данного факта. Но поскольку на меньших значениях параметра функция активации становится практически линейной, функция активации нейронов выходного слоя всех обучаемых в дальнейшем сетей будет заменена на линейную функцию следующего вида:
. (6)
Результаты обучения после изменения функции активации нейронов выходного слоя представлены в таблице 3.
Таблица 3 – Результаты предварительного обучения после изменения функции активации нейронов выходного слоя
|
№ диаг. |
Параметр |
Значение функции ошибок |
|||||
|
Скр. слой |
Вых. слой |
1 |
2 |
3 |
Ср. знач |
СКО |
|
|
7 |
0.0010 |
0.0001 |
19.487100 |
19.467720 |
19.510560 |
19.488460 |
0.021452 |
|
7 |
0.0010 |
0.0050 |
19.680900 |
19.881840 |
19.883880 |
19.815540 |
0.116606 |
|
7 |
0.0010 |
0.0250 |
19.890000 |
19.888980 |
19.888980 |
19.889320 |
0.000589 |
|
7 |
0.0010 |
0.1000 |
19.899180 |
19.917540 |
19.907340 |
19.908020 |
0.009199 |
|
7 |
0.0250 |
0.0001 |
18.805740 |
18.889380 |
18.850620 |
18.848580 |
0.041857 |
|
7 |
0.0250 |
0.0050 |
18.966900 |
19.058700 |
19.029120 |
19.018240 |
0.046857 |
|
7 |
0.0250 |
0.0250 |
19.178040 |
19.244340 |
19.276980 |
19.233120 |
0.050415 |
|
7 |
0.0250 |
0.1000 |
19.758420 |
19.749240 |
19.572780 |
19.693480 |
0.104630 |
|
7 |
0.1000 |
0.0001 |
18.876120 |
18.917940 |
18.930180 |
18.908080 |
0.028347 |
|
7 |
0.1000 |
0.0050 |
18.942420 |
18.774120 |
18.934260 |
18.883600 |
0.094900 |
|
7 |
0.1000 |
0.0250 |
18.927120 |
18.902640 |
18.962820 |
18.930860 |
0.030264 |
|
7 |
0.1000 |
0.1000 |
19.400400 |
19.473840 |
19.380000 |
19.418080 |
0.049355 |
|
7 |
0.5000 |
0.0001 |
18.804720 |
18.966900 |
18.834300 |
18.868640 |
0.086371 |
|
7 |
0.5000 |
0.0050 |
18.954660 |
18.852660 |
18.929160 |
18.912160 |
0.053082 |
|
7 |
0.5000 |
0.0250 |
18.921000 |
18.913860 |
18.936300 |
18.923720 |
0.011465 |
|
7 |
0.5000 |
0.1000 |
19.065840 |
19.151520 |
19.213740 |
19.143700 |
0.074259 |
|
8 |
0.0010 |
0.0001 |
15.020520 |
15.021540 |
15.020520 |
15.020860 |
0.000589 |
|
8 |
0.0010 |
0.0050 |
15.023580 |
15.026640 |
15.020520 |
15.023580 |
0.003060 |
|
8 |
0.0010 |
0.0250 |
15.025620 |
15.028680 |
15.028680 |
15.027660 |
0.001767 |
|
8 |
0.0010 |
0.1000 |
15.062340 |
15.060300 |
15.056220 |
15.059620 |
0.003116 |
|
8 |
0.0250 |
0.0001 |
14.517660 |
14.523780 |
14.563560 |
14.535000 |
0.024922 |
|
8 |
0.0250 |
0.0050 |
14.658420 |
14.590080 |
14.661480 |
14.636660 |
0.040368 |
|
8 |
0.0250 |
0.0250 |
14.924640 |
14.962380 |
14.851200 |
14.912740 |
0.056537 |
|
8 |
0.0250 |
0.1000 |
15.252060 |
15.179640 |
15.155160 |
15.195620 |
0.050388 |
|
8 |
0.1000 |
0.0001 |
14.522760 |
14.501340 |
14.533980 |
14.519360 |
0.016583 |
|
8 |
0.1000 |
0.0050 |
14.578860 |
14.527860 |
14.529900 |
14.545540 |
0.028874 |
|
8 |
0.1000 |
0.0250 |
14.632920 |
14.638020 |
14.578860 |
14.616600 |
0.032783 |
|
8 |
0.1000 |
0.1000 |
15.040920 |
15.034800 |
15.079680 |
15.051800 |
0.024338 |
|
8 |
0.5000 |
0.0001 |
14.498280 |
14.563560 |
14.533980 |
14.531940 |
0.032688 |
|
8 |
0.5000 |
0.0050 |
14.609460 |
14.575800 |
14.621700 |
14.602320 |
0.023768 |
|
8 |
0.5000 |
0.0250 |
14.580900 |
14.594160 |
14.619660 |
14.598240 |
0.019699 |
|
8 |
0.5000 |
0.1000 |
14.764500 |
14.798160 |
14.740020 |
14.767560 |
0.029191 |
|
9 |
0.0010 |
0.0001 |
10.064340 |
10.065360 |
10.065360 |
10.065020 |
0.000589 |
|
9 |
0.0010 |
0.0050 |
10.065360 |
10.065360 |
10.065360 |
10.065360 |
0.000000 |
|
9 |
0.0010 |
0.0250 |
10.073520 |
10.074540 |
10.076580 |
10.074880 |
0.001558 |
|
9 |
0.0010 |
0.1000 |
10.156140 |
10.102080 |
10.132680 |
10.130300 |
0.027108 |
|
9 |
0.0250 |
0.0001 |
10.026600 |
10.026600 |
10.035780 |
10.029660 |
0.005300 |
|
9 |
0.0250 |
0.0050 |
10.069440 |
10.056180 |
10.072500 |
10.066040 |
0.008675 |
|
9 |
0.0250 |
0.0250 |
10.116360 |
10.137780 |
10.161240 |
10.138460 |
0.022448 |
|
9 |
0.0250 |
0.1000 |
10.228560 |
10.285680 |
10.217340 |
10.243860 |
0.036649 |
|
9 |
0.1000 |
0.0001 |
9.976620 |
10.024560 |
10.028640 |
10.009940 |
0.028928 |
|
9 |
0.1000 |
0.0050 |
10.050060 |
10.030680 |
10.057200 |
10.045980 |
0.013723 |
|
9 |
0.1000 |
0.0250 |
10.100040 |
10.123500 |
10.114320 |
10.112620 |
0.011822 |
|
9 |
0.1000 |
0.1000 |
10.168380 |
10.214280 |
10.305060 |
10.229240 |
0.069557 |
|
9 |
0.5000 |
0.0001 |
10.017420 |
10.039860 |
10.044960 |
10.034080 |
0.014652 |
|
9 |
0.5000 |
0.0050 |
10.066380 |
10.023540 |
10.058220 |
10.049380 |
0.022747 |
|
9 |
0.5000 |
0.0250 |
10.086780 |
10.111260 |
10.096980 |
10.098340 |
0.012297 |
|
9 |
0.5000 |
0.1000 |
10.124520 |
10.167360 |
10.162260 |
10.151380 |
0.023401 |
|
10 |
0.0010 |
0.0001 |
6.705480 |
6.705480 |
6.705480 |
6.705480 |
0.000000 |
|
10 |
0.0010 |
0.0050 |
6.707520 |
6.706500 |
6.706500 |
6.706840 |
0.000589 |
|
10 |
0.0010 |
0.0250 |
6.715680 |
6.720780 |
6.706500 |
6.714320 |
0.007236 |
|
10 |
0.0010 |
0.1000 |
6.746280 |
6.737100 |
6.727920 |
6.737100 |
0.009180 |
|
10 |
0.0250 |
0.0001 |
6.705480 |
6.705480 |
6.705480 |
6.705480 |
0.000000 |
|
10 |
0.0250 |
0.0050 |
6.714660 |
6.711600 |
6.714660 |
6.713640 |
0.001767 |
|
10 |
0.0250 |
0.0250 |
6.777900 |
6.746280 |
6.735060 |
6.753080 |
0.022215 |
|
10 |
0.0250 |
0.1000 |
6.869700 |
6.856440 |
6.866640 |
6.864260 |
0.006943 |
|
10 |
0.1000 |
0.0001 |
6.705480 |
6.705480 |
6.705480 |
6.705480 |
0.000000 |
|
10 |
0.1000 |
0.0050 |
6.712620 |
6.710580 |
6.707520 |
6.710240 |
0.002567 |
|
10 |
0.1000 |
0.0250 |
6.789120 |
6.739140 |
6.760560 |
6.762940 |
0.025075 |
|
10 |
0.1000 |
0.1000 |
6.919680 |
6.915600 |
6.971700 |
6.935660 |
0.031278 |
|
10 |
0.5000 |
0.0001 |
6.705480 |
6.705480 |
6.705480 |
6.705480 |
0.000000 |
|
10 |
0.5000 |
0.0050 |
6.711600 |
6.710580 |
6.710580 |
6.710920 |
0.000589 |
|
10 |
0.5000 |
0.0250 |
6.721800 |
6.762600 |
6.749340 |
6.744580 |
0.020812 |
|
10 |
0.5000 |
0.1000 |
6.908460 |
6.888060 |
6.866640 |
6.887720 |
0.020912 |
Для большей наглядности изобразим полученные по функции ошибок данные в графическом виде. На рисунке 3 отчетливо видно, что наилучших результатов искусственные нейронные сети добились при значениях параметра наклона функции активации для нейронов выходного слоя из диапазона от 0.0001 до 0.0010. Изобразим при этом на отдельных графиках зависимость значений функции ошибок от значений параметра наклона функции активации для нейронов скрытого слоя (рисунок 4).
Рисунок 3 – График зависимости значения функции ошибок от параметров функций активации
Рисунок 4 – График зависимости значения функции ошибок от параметра функции активации нейронов скрытого слоя
Исходя из полученных данных, дальнейшее уменьшение значения параметра наклона функции активации для нейронов выходного слоя не целесообразно, поскольку уже при значениях 0.0010 и 0.0001 разница в значениях функции ошибок не столь велика.
Заключение
На основании представленных данных можно сделать следующие выводы:
1) при внедрении цифровых водяных знаков в графические изображения следует использовать искусственные нейронные сети типа многослойный персептрон;
2) функция активации нейронов выходного слоя является линейной и параметр ее наклона равен 0.0001;
3) функция активации нейронов скрытого слоя является нелинейной и значение параметра ее наклона различно для нейронных сетей, соответствующих разным диагоналям ДКП матрицы:
- для 7-ой диагонали – 0.0500;
- для 8-ой диагонали – 0.1000;
- для 9-ой диагонали – 0.1000;
- для 10-ой диагонали – 0.2500.
Литература:
1. Конахович
Г.Ф., Пузыренко А.Ю. Компьютерная стеганография: Теория и практика. – М.: МК-Пресс,
2006. – 283 с.
2. E. Koch,
J. Zhao. Towards Robust and Hidden Image Copyright Labeling. IEEE Workshop on
Nonlinear Signal and Image Processing. 1995. P. 123-132.
3. О.П. Солдатова, С.С. Байков. Практическое применение нейронных сетей для решения задач классификации и идентификации – Электронный научный журнал «Исследовано в России», 2006. – zhurnal.ape.relarn.ru/articles/ 2006/135.pdf
4. Электронный учебник StatSoft: Нейронные сети. – www.statsoft.ru/ home/textbook/modules/stneunet.html
5. Многослойный персептрон – Проект www.aiportal.ru. Портал искусственного интеллекта. – www.aiportal.ru/articles/neural-networks/multi-perceptron.html
6. В.А. Головко. Нейроинтеллект: теория и применения. Книга 1: Организация и обучение нейронных сетей с прямыми и обратными связями. – Брест: БПИ, 1999. – 260 с.
7. А.Н. Колмогоров. О представлении непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных // ДАН СССР. – 1956. – Т. 108. – С. 2.
8. А.Н. Колмогоров. О представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения // ДАН СССР. – 1957. – Т. 114. – С. 953-956.
9. R. Hecht-Nielsen.
Kolmogorov’s mapping neural network existence theorem // IEEE First Annual Int.
Conf. on Neural Networks, San Diego, 1987. Vol. 3. – P. 11-13.
10. Функции активации в нейронных сетях – Проект
www.aiportal.ru. Портал искусственного интеллекта. – www.aiportal.ru/articles/neural-networks/
activation-function.html
11. А. Шахиди. Алгоритм обучения RPROP – математический аппарат. – www.basegroup.ru/library/analysis/neural/rprop/