Кудинов Ю.И., Келина А.Ю.
Липецкий государственный технический университет
СРАВНЕНИЕ ЛИНЕЙНОГО И НЕЧЕТКОГО ПИД
РЕГУЛЯТОРОВ
В данной работе сравнивается качество
переходных процессов двух систем регулирования температуры в водяной ванне: с
линейным и нечетким пропорционально- интегрально-дифференциальными (ПИД) регуляторами.
Система регулирования температуры в
водяной ванне с мешалкой (М), приведена на рис. 1. Сигнал от датчика (Д),
пропорциональный температуре воды, подается на термоэлектрический преобразователь
(ТЭП), далее в виде электрического напряжения на аналого-цифровой
преобразователь (АЦП) и наконец, в цифровой форме в микро-ЭВМ, реализующую линейный
и нечеткий ПИД регуляторы. Управляющий сигнал (УС) от микро-ЭВМ, поступая
на тиристор (Т), меняет электрическое напряжение, питающее нагреватель (Н). Для
получения переходных процессов используется дискретная модель объекта управления
- водяной ванны, полученная в работе [1]. Изменение температуры воды
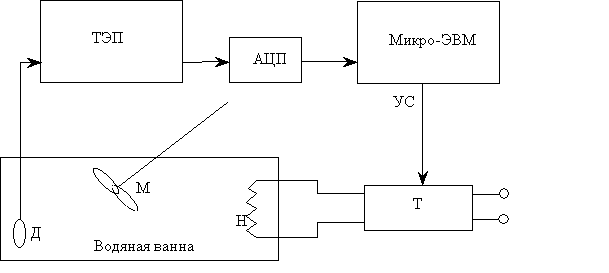
Рис. 1. Схема установки
в водяной ванне описывается дифференциальным уравнением
 , (1)
, (1)
где y(t) – выходная температура в системе в градусах С0;
u(t) – тепло,
входящее в систему; y(0) – комнатная температура. Полагая, что эквиваленты теплоёмкости Ст и термического сопротивления R
являются константами, в дискретной форме дифференциальное
уравнение (1), описывающее изменение температуры в водяной ванне, будет иметь
вид
 , (2)
, (2)
 где α
= 1.0015·10-4 и β
= 8.67973·10-3 – константы, описывающие R и C; y(0) = 25; u(t) – напряжение, поступающее к нагревателю в пределах от 0 до 5 В; Ts= 30 – период дискретизации. На рис. 2 показана упрощенная схема
замкнутой системы управления, в которой измерение выхода
где α
= 1.0015·10-4 и β
= 8.67973·10-3 – константы, описывающие R и C; y(0) = 25; u(t) – напряжение, поступающее к нагревателю в пределах от 0 до 5 В; Ts= 30 – период дискретизации. На рис. 2 показана упрощенная схема
замкнутой системы управления, в которой измерение выхода ![]() и определение
и определение
Рис.2. Схема замкнутой системы управления
управляющего воздействия ![]() ПИД регулятором осуществляются в дискретные моменты времени
ПИД регулятором осуществляются в дискретные моменты времени
![]() ,
, ![]() , обозначенные через
, обозначенные через ![]() . На выходе элемента сравнения (ЭС) формируется
дискретная ошибка
. На выходе элемента сравнения (ЭС) формируется
дискретная ошибка ![]() , равная отклонению текущего значения выхода
, равная отклонению текущего значения выхода ![]() от заданного
от заданного ![]() (k) и поступающая на вход
регулятора. Вначале по формуле (2) в Excel рассчитываются массивы
(k) и поступающая на вход
регулятора. Вначале по формуле (2) в Excel рассчитываются массивы ![]() и
и ![]() , после чего они экспортируются в MATLAB, в котором определяется
передаточная функция объекта управления
по каналу напряжение на нагревателе - температура водяной ванны
, после чего они экспортируются в MATLAB, в котором определяется
передаточная функция объекта управления
по каналу напряжение на нагревателе - температура водяной ванны
 . (3)
. (3)
Средствами MATLAB методом Такахаши по кривой разгона
[2] вычисляются коэффициенты дискретного уравнения ПИД-регулятора ![]() = 13.05,
= 13.05, ![]() = -20.3,
= -20.3, ![]() = 7.25, на основании которого и передаточной функции объекта
(3) в Simulink строится модель дискретной замкнутой системы стабилизации температуры
водяной ванны (рис. 3).
= 7.25, на основании которого и передаточной функции объекта
(3) в Simulink строится модель дискретной замкнутой системы стабилизации температуры
водяной ванны (рис. 3).
![]()
![]()
![]()
![]()
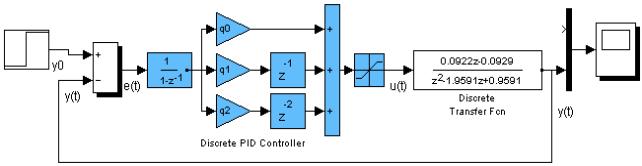
Рис. 3. Система управления с линейным ПИД регулятором
По графику переходного
процесса в замкнутой системе управления (рис. 4) при ступенчатом изменении
задания ![]() (k) видно, что используемый ПИД –
регулятор не обеспечивает удовлетворительное качество переходного процесса.
Средняя модульная ошибка регулирования, рассчитанная по формуле
(k) видно, что используемый ПИД –
регулятор не обеспечивает удовлетворительное качество переходного процесса.
Средняя модульная ошибка регулирования, рассчитанная по формуле
 / y0(k),
/ y0(k),
 равна
J = 0.13. Последующее
уточнение параметров ПИД – регулятора с
использованием оптимизационных методов существенно не улучшило результат J = 0.11.
равна
J = 0.13. Последующее
уточнение параметров ПИД – регулятора с
использованием оптимизационных методов существенно не улучшило результат J = 0.11.
Рис. 4. Переходный процесс
Таким образом, традиционные линейные
ПИД регуляторы далеко не всегда обеспечивают удовлетворительное качество регулирования,
поэтому в качестве сравнения построим систему управления с тем же объектом и
нечетким ПИД регулятором.
Для этих целей воспользуемся средствами нечеткого моделирования, реализованными
в среде MATLAB и Simulink. В уже построенной модели дискретной замкнутой
системы управления в Simulink с помощью графических средств пакета Fuzzy Logic Toolbox добавим нечеткий регулятор Fuzzy
Logic Controller with Ruleviewer (рис. 5).
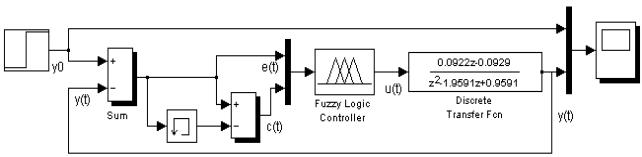
Рис. 5. Система управления с нечетким ПИД регулятором
![]() Нечеткий ПИД
регулятор строится в редакторе систем нечеткого вывода FIS Editor. Для этого в FIS-редакторе создается система нечеткого вывода типа Mamdani с двумя входами и одним выходом, поскольку для
системы управления температурой водяной ванны
Нечеткий ПИД
регулятор строится в редакторе систем нечеткого вывода FIS Editor. Для этого в FIS-редакторе создается система нечеткого вывода типа Mamdani с двумя входами и одним выходом, поскольку для
системы управления температурой водяной ванны
 указываются
две входные переменные: ошибка e(k) = y0(k) - y(k), представляющая собой рассогласование между заданной y0(k) и фактической y(k) температурой воды, и скорость
изменения ошибки c(k) = e(k) - e(k-1). Выходом является сигнал (напряжение) u(k), подаваемый
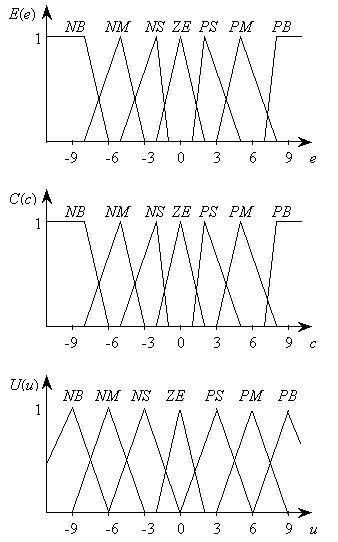
на нагреватель. После этого интервалы изменения указанных трех переменных
представляются в виде семи нечетких подмножеств с лингвистическими значениями, NM среднее отрицательное, NS малое отрицательное, ZE нулевое, PS малое
положительное, PM среднее положительное,
PB большое положительное, треугольные
и трапецеидальные функции принадлежности которых E(e), C(c) и U(u), изображены на рис. 6. Нечеткие
правила ПИД закона регулирования, приведены ниже в табличной форме.
указываются
две входные переменные: ошибка e(k) = y0(k) - y(k), представляющая собой рассогласование между заданной y0(k) и фактической y(k) температурой воды, и скорость
изменения ошибки c(k) = e(k) - e(k-1). Выходом является сигнал (напряжение) u(k), подаваемый
на нагреватель. После этого интервалы изменения указанных трех переменных
представляются в виде семи нечетких подмножеств с лингвистическими значениями, NM среднее отрицательное, NS малое отрицательное, ZE нулевое, PS малое
положительное, PM среднее положительное,
PB большое положительное, треугольные
и трапецеидальные функции принадлежности которых E(e), C(c) и U(u), изображены на рис. 6. Нечеткие
правила ПИД закона регулирования, приведены ниже в табличной форме.
|
|
NB |
NM |
NS |
ZE |
PS |
PM |
PB |
|
PB |
|
|
|
PB |
PB |
PB |
PB |
|
PM |
|
|
|
PM |
PM |
PM |
PB |
|
PS |
|
|
PS |
PS |
PS |
PM |
PB |
|
ZE |
NB |
NM |
NS |
ZE |
PS |
PM |
PB |
|
NS |
|
|
NS |
NS |
NS |
|
|
|
NM |
|
|
|
NM |
|
|
|
|
NB |
|
|
|
NB |
|
|
|
Например, выделенная ячейка определяет следующее правило:
Если e(k) есть PS, с(k) есть PB , то u(k) есть PB
В диалоговых
окнах FIS-редактора выбираются тип нечеткого вывода, термы и вид
функций принадлежности для двух входных и одной выходной переменной системы, а
также нечеткие правила. После запуска процесса моделирования в среде Simulink системы управления с нечетким ПИД
регулятором температуры наблюдается
существенное улучшение качества переходного процесса J = 0.052. Таким образом, в ряде случаев применение нечеткого
ПИД регулятора может оказаться более целесообразным, чем линейного ПИД регулятора.
Литература
1.
Омату С., Халид М., Юсоф
Р. Нейроуправление и его приложения. Кн. 2. – М.: ИПРЖР, 2000. – 272 с.
2.
Takahashi Y., Chan C.S., Auslander D.M. Parametereinstellung bei linearen DDC-Algorithmen// Regelungstechnic and Prozessdatenverarbeitung 1971, №19, P
237-244